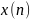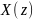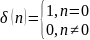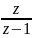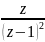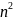- •Часть 2
- •Часть 2
- •Введение
- •1. Элементы комбинаторики
- •1.1. Простейшие комбинаторные конфигурации
- •Основные правила комбинаторики
- •Выборки элементов без повторений
- •Выборки элементов с повторениями
- •Латинские прямоугольники, конечные проективные плоскости и блок-схемы
- •1.2.1. Латинские прямоугольники
- •1.2.2. Конечные проективные плоскости
- •1.2.3. Блок-схемы
- •Формула включений и исключений
- •Объединение комбинаторных конфигураций
- •1.3.2. Принцип включения и исключения
- •1.3.3. Число булевых функций, существенно зависящих от всех своих переменных
- •1.3.4. Решето Эратосфена
- •Рекуррентные уравнения
- •1.4.1. Определение рекуррентного уравнения
- •1.4.2. Решение линейного однородного рекуррентного уравнения
- •1 (2) .4.3. Решение линейного неоднородного рекуррентного уравнения
- •1.5. Производящие функции
- •1.5.1. Общие сведения о производящих функциях
- •1.5.2. Производящая функция для биноминальных коэффициентов
- •1.5.3. Производящая функция для чисел Фибоначчи
- •1.6.1. Определение z – преобразования
- •1.6.2. Обратное z – преобразование
- •В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.
- •1.6.3. Свойства z-преобразования
- •1.6.4. Использование z-преобразований для решения рекуррентных уравнений
- •1.6.5. Таблица односторонних z-преобразований
- •1.7. Трансверсали и перманенты
- •1.7.1. Множества и мультимножества
- •1.7.2. Трансверсали
- •1.7.3. Пермамент матрицы
- •1.7.4. Число трансверсалей
- •1.8. Матрицы Адамара
- •1.8.1. Определение матрицы Адамара и ее свойства
- •1.8.2. Эквивалентные преобразования матриц Адамара
- •1.8.3. Построение матриц Адамара
- •2. Основы теории конечных автоматов
- •2.1. Понятие конечного автомата
- •2.1.1. Общие сведения о конечных автоматах
- •2.1.2. Абстрактное определение конечного автомата
- •2.2. Эквивалентности в автоматах
- •2.2.1. Основные определения
- •2.2.2. Покрытия и морфизмы
- •2.2.3. Эквивалентные состояния автоматов
- •2.3. Процедура минимизации конечных автоматов
- •2.4. Автоматные функции и эксперименты с автоматами
- •2.4.1. Понятие ограниченно детерминированной функции
- •2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •2.4.3. Пример реализации конечного автомата с помощью сфэз
- •2.4.4. Эксперименты с автоматами
- •2.5. Автоматные языки
- •2.5.1. Представление о формальных языках
- •2.5.2. Алфавит, слово, язык
- •2.5.3. Классификация грамматик и языков
- •2.5.4. Понятие формальной грамматики
- •2.5.5. Автоматные грамматики
- •2.6. Модификации конечных автоматов
- •2.6.1. Частичные автоматы
- •2.6.2. Понятия недетерминированного и вероятностного автоматов
- •2.7. Процедура минимизации частичного автомата
- •2.7.1. Совместимые состояния
- •2.7.2. Техника определения совместимых состояний
- •2.7.3. Построение минимального автомата
- •3. Введение в нечеткую математику
- •3.1. Нечёткие множества
- •3.2. Нечеткие отношения
- •3.3. Нечеткая логика
- •Заключение
- •Библиографический список
- •Оглавление
- •2.7.3. Построение минимального автомата 98
- •Часть 2
- •394026 Воронеж, Московский просп., 14
- •Часть 2
1.6.3. Свойства z-преобразования
1)
Линейности -–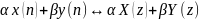
2)
Задержки -–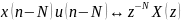
где
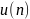 – функция единичного скачка
– функция единичного скачка
3)
Умножения на экспоненту -–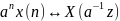
4)
Умножения на n -–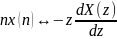
5)
Опережающего сдвига -–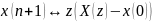
6)
Свертки -–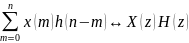
Указанные свойства упрощают получение преобразований и их обращений.
1.6.4. Использование z-преобразований для решения рекуррентных уравнений
В качестве примера рассмотрим рекуррентное уравнение первого порядка
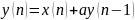 с начальным условием
с начальным условием
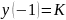
Пусть на вход поступает последовательность (правая часть рекуррентного уравнения)
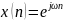
Умножаем
обе части рекуррентного уравнения на
величину
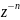 и просуммируем по n от 0 до
и просуммируем по n от 0 до
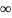 :
:
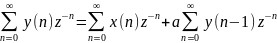
Используя свойство задержки, имеем
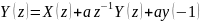
Откуда
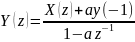
Т.к.
,
то
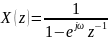
То
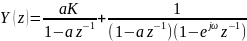
Разложив второе слагаемое на простые дроби, получим
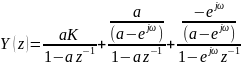
Вычислим обратное Z-преобразование
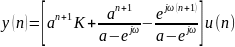 .
.
Первое слагаемое в скобках представляет собой составляющую отклика, определяемую начальными условиями, а второе – переходную характеристику системы. Третье слагаемое описывает вынужденные колебания в системе.
1.6.5. Таблица односторонних z-преобразований
Таблица 4
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Продолжение табл. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
1.7. Трансверсали и перманенты
1.7.1. Множества и мультимножества
Не существует формального определения множества; считается, что это понятие первичное и не определяется. Так, можно говорить, что множество есть объединение различных элементов, но при этом мы оставляем неопределяемыми понятия "объединение" и "элементы". Дадим следующее определение множеству: множество - это неупорядоченная совокупность различных объектов или структура данных, используемая для представления множества. Мультимножество есть объединение не обязательно различных элементов; его можно считать множеством, в котором каждому элементу поставлено в соответствие положительное целое число, называемое кратностью.
Конечное множество S будем записывать в следующем виде:
S = {s1, s2, …, sn}
где s1, s2, …, sn - элементы S, обязательно различные! Мощность множества S обозначается как |S|, для выписанного выше множества мощность записывается так |S| = n. Если S- конечное мультимножество, то будем записывать его в следующем виде:
S = {s1, s1, …, s1, s2, s2, …, s2,s3…, s3} = {m1*s1,m2*s2,mn*sn }
m1 раз m2 раз m3 раз
Здесь все Si различны и mi- кратность элемента si. В этом случае мощность S равна
|S| = ∑mi (i = 1..n)
Наиболее
общими операциями на множествах и
мультимножествах являются операции
объединения
и пересечения.
Для множеств эти операции будем обозначать
 и
и
 ,
а для мультимножеств
,
а для мультимножеств
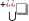 и
и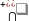 . Последовательное и связанное
представление последовательностей
можно использовать для множеств и
мультимножеств очевидным способом.
Индуцируя искусственный порядок
элементов множества, или используя
собственный порядок, если он существует,
можно рассматривать множество как
последовательность. Аналогично, как
последовательность можно рассматривать
и мультимножество, или, для того чтобы
сэкономить место, его можно рассматривать
как последовательность пар, каждая из
которых состоит из элемента и его
кратности.
. Последовательное и связанное
представление последовательностей
можно использовать для множеств и
мультимножеств очевидным способом.
Индуцируя искусственный порядок
элементов множества, или используя
собственный порядок, если он существует,
можно рассматривать множество как
последовательность. Аналогично, как
последовательность можно рассматривать
и мультимножество, или, для того чтобы
сэкономить место, его можно рассматривать
как последовательность пар, каждая из
которых состоит из элемента и его
кратности.
Как и для последовательностей, наилучший метод представления множеств или мультимножеств существенно зависит от операций, которые выполняются над ними. Предположим, например, что имеем дело с непересекающимися подмножествами множества S = {s1, s2, …, sn} и что над ними необходимо выполнить две следующие операции: объединение двух множеств и отыскание подмножества, содержащего данное si. Таким образом, в любой момент времени имеем разбиение S на непустые непересекающиеся подмножества. Рассмотрим эти операции в конце данной лекции.
С
целью идентификации считаем, что каждое
из непересекающихся подмножеств
множества S
имеет имя. Имя
- это просто один из элементов подмножества,
или, иначе, - представитель подмножества.
Когда мы будем ссылаться на имя
подмножества, то будем под этим
подразумевать его представителя.
Рассмотрим, например, множество
 разбитое на четыре непересекающихся
подмножества {1, 6, [7], 8, 11}, {[3], 4, 5}, {[2]}, {9,
[10]}.
разбитое на четыре непересекающихся
подмножества {1, 6, [7], 8, 11}, {[3], 4, 5}, {[2]}, {9,
[10]}.
В каждом из подмножеств, взятый в скобки элемент является его именем. Если нам нужно найти подмножество, в котором содержится восьмерка, искомым ответом будет 7, то есть имя подмножества, содержащего восьмерку. Если нужно взять объединение подмножеств с именами 2 и 10, получим разбиение множества S следующего вида:
{1,
6, [7], 8, 11}, {[3], 4, 5}, {[2]}![]() {9, 10]}
{9, 10]}
Именем множества {[2]} {9, 10]} может быть или 2, или 10. Предполагаем, что вначале имеется разбиение множества S = {s1, s2, …, sn} на nподмножеств, каждое из которых состоит из одного элемента
{[s1], [s2], …, [sn]}
и имя каждого из них есть просто этот единственный элемент. Это разбиение преобразуется путем применения операций объединения вперемешку с операциями отыскания. Такая кажущаяся на первый взгляд надуманной задача чрезвычайно полезна в определенных комбинаторных алгоритмах; пример ее полезности виден в "жадном" алгоритме.