Некоторые приложения.

Пример 2.13.

Функция полезности ЛПР имеет вид u(w) = -e^-5w. Для принимающего решения имеется две случайные экономические возможности. Первая из них, обозначаемая через Х, имеет нормальное распределение со средним 5 и дисперсией 2. Говоря о нормальном распределении со средним µ и с дисперсией σ², пользуются сокращенной записью N(µ,σ²). Другая возможность, обозначаемая через Y, имеет распределение N(6;2,5). Какую возможность следует предпочесть?

Решение.

Если случайная величина Х имеет нормальное распределение N(µ,σ²), то производящая функция моментов имеет вид:

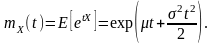
Используя это выражение получим:

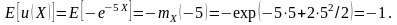
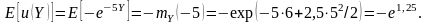
Таким образом,

и распределение с.в. Х предпочтительнее распределения с.в. Y.

В данном примере с.в. Х предпочтительнее, чем Y, несмотря на то, что µ_Х = 5 < µ_Y = 6. Поскольку принимающий решение не склонен к риску, тот факт, что распределение с.в. Y более «размазано», чем распределение с.в. Х, свидетельствует против распределения с.в. Y при оценки его желательности. Если с.в. Y имеет распределение N(6; 2,4), то Е[u(Y)] = -1 и для принимающего решения будет безразлично, выбрать распределение Х или распределение Y.

Пример 2.14.

Функция полезности лица, принимающего решения, задается выражением

u(w) = w - 0,01w², w < 50.

Принимающий решения сохранит капитал w с вероятностью р и будет нести финансовые потери величины X с вероятностью q = 1 - р. Для значений w, X и р, указанных в приведенной ниже таблице, найдем максимальную страховую премию, которую принимающий решения готов заплатить за полное страховое покрытие. Предположим, что X ≤ w < 50.

Решение.

Для нашей задачи формула (2.4.7) приобретает вид

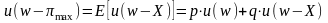
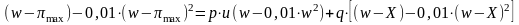
Для заданных значений w, X и р эта формула становится квадратным уравнением. Ниже приведены два его решения.

Капитал (w)	Потери (X)	Вероятность (p)	Страховая премия (π) ((πmax)
10	10	0,5	5,28
20	10	0,5	5,37

В примере, как и ожидалось, π_max превосходит величину ожидаемых потерь, EX = 5. Однако максимальная страховая премия за потери с одним и тем же распределением растет с ростом капитала лица, принимающего решения. Этот результат кажется неестественным тем, кто считает, что более типичным поведением было бы уменьшение суммы, которую принимающий решения готов выплачивать за страхование, поскольку при увеличении капитала он мог бы позволить себе больший риск. К сожалению, рост максимальной страховой премии с ростом капитала является характеристической чертой квадратичной функции полезности. Поэтому тем из принимающих решения лиц, которые полагают, что их способность брать на себя случайные потери растет с ростом капитала, не следует выбирать такие функции полезности.

Если мы рассмотрим пример (2.11), используя показательную функцию полезности, то, как мы знаем, премия π_max не будет зависеть от w, величины капитала. Так, если u(w) = -e^-0,01w, то можно показать, что π_max = 5,12 как при w = 10, так и при w = 20.

Пример 2.15.

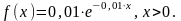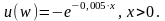Вероятность того, что собственности не будет нанесен ущерб за времени, равняется 0,75. Функция плотности возможных положительных потерь задается соотношением Функция полезности владельца собственности имеет вид Вычислим ожидаемые потери и максимальный размер страховой премии, которую владелец собственности готов заплатить за полное страховое покрытие.

Решение.

Ожидаемые потери задаются формулой

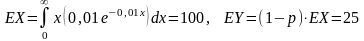
Рассчитаем максимальную премию, которую владелец собственности выплатит за такой страховой договор.

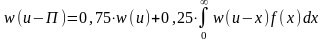
Т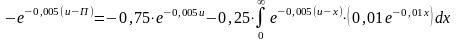

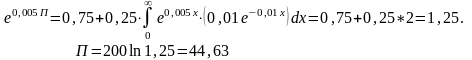
Таким образом, владелец собственности готов заплатить сумму, превышающую ожидаемые частичные потери, самое большее, на величину

44,63 – 25 = 19,63.