1. Однослойный персептрон

Круг проблем, которые под силу однослойному персептрону, очень ограничен. Рассмотрим однослойную сеть из одного нейрона (рис ).

Рис. . Сеть из одного нейрона

Выход сети задается функцией y  Fw₁x₁  w₂x₂  . Если F имеет вид жесткой ступеньки с двумя возможными значениями, 0 и 1, то выход сети будет иметь вид (рис. ).

Рис. . Решающая поверхность однослойного персептрона

Гиперплоскость (в случае многих входов), разделяющая различные значения выхода, называется решающей поверхностью. Для жесткой ступеньки решающая поверхность задается уравнением:

w₁x₁  w₂x₂  

Для двухвходового нейрона она имеет вид прямой, произвольно повернутой и смещенной из начала координат. Угол поворота определяется коэффициентами w₁, w₂, а смещение из начала коорди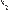нат — порогом  .

Если выбрана гладкая функция активации, то выход сети будет плавно меняться от нуля до единицы в направлении, перпендикулярном прямой.

2. Двухслойный персептрон

Двухслойный персептрон с двумя входами и одним выходом представлен на рис. .

Пусть функция активации — жесткая ступенька с двумя возможными значениями. Решающая поверхность является пересечением, объединением, инверсией или их комбинацией от областей, создаваемых тремя нейронами в первом слое. Вид функции (пересечение, объединение, инверсия или их комбинация) определяется параметрами нейрона второго слоя (порогом и весами). Если моделируется пересечение, то такая двухслойная сеть может сформировать произвольную выпуклую многоугольную односвязную решающую область. Число сторон в многоугольнике совпадает с количеством нейронов в слое 1. В зависимости от вида комбинирования областей, а также от положения гиперплоскостей область может быть открытой или закрытой. Если область закрытая, то она всегда имеет вид выпуклого многоугольника. Пример открытой области, полученной объединением областей первого слоя — на рис.

Первый слой содержит 4 нейрона, их выходы обозначены y₁, ..., y₄. Выход сети получается объединением выходов первого слоя операцией "ИЛИ". Серым цветом показана область, в которой выход сети равен единице.

Рис. . Открытая область, сформированная двухслойным персептроном.

Для гладкой непрерывной функции активации результаты аналогичные, но нет четких линий, отделяющих области друг от друга. Картина "расплывается".

3. Трехслойный персептрон

Трехслойный персептрон является наиболее общим в своем классе сетей и способен формировать произвольные многоугольные невыпуклые многосвязные области. Нейроны первых двух слоев создают произвольные независимые многоугольные решающие области в нужном количестве и в нужных измерениях входного пространства X. Эти области объединяются нейронами третьего слоя в нужной комбинации. Как и для двухслойного персептрона, допускаются операции пересечения и объединения. Весовые коэффициенты могут быть отрицательными, и соответствующая область может входить со знаком минус, что реализует операцию инверсии. Результирующая область может быть открытой.

Пример решающей области для жесткой нелинейности в нейронах показан на рис. . Первый и второй слой формируют независимые подобласти S₁, S₂, S₃. Единственный нейрон третьего слоя объединяет их по закону S₁  S₃  S₂. Весовой коэффициент нейрона в третьем слое, соответствующий подобласти S₂, имеет знак " – ", и поэтому перед областью S₂ стоит знак отрицания.

Решающая область для трехслойного персептрона с жесткой нелинейностью

Проблема функции «исключающее ИЛИ»

Наглядной иллюстрацией ограниченности для однослойного персептрона является функция "исключающее ИЛИ". Эта булева функция от двух переменных принимает значение "истина", когда значения входных переменных различны, и "ложь" — в противном случае. Другими словами она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рис. 2.4. Обозначим один вход через х, а другой через у, тогда все их возможные комбинации будут состоять из четырех точек на плоскости х-у, как показано на рис. 2.5. Например, точка х = 0 и у = 0 обозначена на рисунке как точка А₀.

Рис. 2.4. Однонейронная система

Рис. 2.5. Проблема "исключающее ИЛИ"

Табл. 2.1 показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены А₀ и А₁, единичный выход – В₀ и В₁.

Таблица 2.1. Таблица истинности для функции "исключающее ИЛИ"

Точки	Значения х	Значения у	Требуемый выход
A0	0	0	0
B0	1	0	1
B1	0	1	1
A1	1	1	0

В сети на рис. 2.4 функция F является обычным порогом, так что OUT принимает значение ноль, когда NET меньше 0,5, и единица в случае, когда NET больше или равно 0,5. Нейрон выполняет следующее вычисление:

NET = xw₁ + yw₂ (2.1)

Никакая комбинация значений двух весов не может дать соотношения между входом и выходом, задаваемого табл. 2.1. Чтобы понять это ограничение, зафиксируем NET на величине порога 0,5. Сеть в этом случае описывается уравнением (2.2).

xw₁ + yw₂ = 0,5 (2.2)

Это уравнение линейно по х и у, т. е. все значения по х и у, удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости х-у.

Любые входные значения для х и у на этой линии будут давать пороговое значение 0,5 для NET. Входные значения с одной стороны прямой обеспечат значения NET больше порога, следовательно, OUT=1. Входные значения по другую сторону прямой обеспечат значения NET меньше порогового значения, делая OUT равным 0. Изменения значений w₁, w₂ и порога будут менять наклон и положение прямой. Для того чтобы сеть реализовала функцию "исключающее ИЛИ", заданную табл. 2.1, нужно расположить прямую так, чтобы точки А были с одной стороны прямой, а точки В – с другой. Попытавшись нарисовать такую прямую на рис. 2.5, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции "исключающее ИЛИ".

Обучение многослойного персептрона

Алгоритм обратного распространения ошибки

Возьмем двухслойную сеть (рис. 1) (входной слой не рассматривается).

Рис. 1.  Пример двухслойной нейронной сети

Веса нейронов первого (скрытого) слоя пометим верхним индексом (1), а выходного слоя - верхним индексом (2). Выходные сигналы скрытого слоя обозначим , а выходного слоя - . Будем считать, что функция активации нейронов задана в сигмоидальной униполярной или биполярной форме. Для упрощения описания будем использовать расширенное обозначение входного вектора сети в виде , где соответствует порогу. С вектором связаны два выходных вектора сети: вектор фактических выходных сигналов и вектор ожидаемых выходных сигналов .

Цель обучения состоит в подборе таких значений весов и для всех слоев сети, чтобы при заданном входном векторе получить на выходе значения сигналов , которые с требуемой точностью будут совпадать с ожидаемыми значениями для . Выходной сигнал -го нейрона скрытого слоя описывается функцией

В выходном слое -й нейрон вырабатывает выходной сигнал

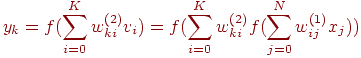
Из формулы следует, что на значение выходного сигнала влияют веса обоих слоев, тогда как сигналы, вырабатываемые в скрытом слое, не зависят от весов выходного слоя.

Основу алгоритма обратного распространения ошибки составляет целевая функция, формулируемая, как правило, в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов. Для обучающей выборки, состоящей из примеров, целевая функция имеет вид

Минимизация целевой функции достигается уточнением вектора весов (обучением) по формуле

где

(1)

- коэффициент обучения, а - направление в пространстве весов . Выбор этого направления обычно основан на определении градиента целевой функции относительно весов всех слоев сети. Для весов выходного слоя задача имеет очевидное решение. Для других слоев используется алгоритм обратного распространения ошибки. Рассмотрим его на примере двухслойной сети. В этом случае при целевая функция определяется выражением

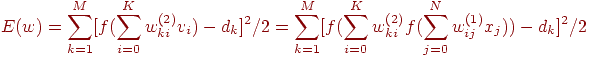(2)

Компоненты градиента рассчитываются дифференцированием зависимости (2). В первую очередь определяются веса нейронов выходного слоя. Для выходных весов получаем:

где

Если ввести обозначение

то соответствующую компоненту градиента относительно весов выходного слоя можно представить в видеъ

(3)

Компоненты градиента относительно нейронов скрытого слоя определяются так же, но описываются более сложной зависимостью, следующей из существования функции, которая задана в виде

Отсюда получаем

Если ввести обозначение

то получим выражение, определяющее компоненты градиента относительно весов нейронов входного слоя в виде

(4)

В обоих случаях (формулы (3) и (4)) описания градиента имеют аналогичную структуру и представляются произведением двух сигналов: первый соответствует начальному узлу данной взвешенной связи, а второй — величине погрешности, перенесенной на узел, с которым эта связь установлена. Определение вектора градиента важно для последующего процесса уточнения весов. В классическом алгоритме обратного распространения ошибки вектор в выражении (1) задает направление антиградиента (метод наискорейшего спуска), поэтому

В соответствии с алгоритмом обратного распространения ошибки в каждом цикле обучения выделяются следующие этапы:

1. Анализ нейронной сети в прямом направлении передачи информации при генерации входных сигналов, составляющих очередной вектор . В результате такого анализа рассчитываются значения выходных сигналов нейронов скрытых слоев и выходного слоя, а также соответствующие производные функций активации каждого слоя ( - количество слоев сети).

2. Создание сети обратного распространения ошибок путем изменения направлений передачи сигналов на обратные, замена функций активации их производными и подача на бывший выход (а в настоящий момент - вход) сети сигнала в виде разности между фактическим и ожидаемым значением. Для определенной таким образом сети необходимо рассчитать значения требуемых обратных разностей.

3. Уточнение весов (обучение сети) производится по предложенным выше формулам для оригинальной сети и для сети обратного распространения ошибки.

4. Описанный процесс следует повторить для всех обучающих примеров задачника, продолжая его вплоть до выполнения условия остановки алгоритма. Действие алгоритма завершается в момент, когда норма градиента упадет ниже априори заданного значения, характеризующего точность процесса обучения.

Для определения всех компоненты градиента целевой функции, т.е. всех частных производных функции по весам сети, необходимо двигаясь от входов сети (бывших выходов), перемножить все встречающиеся на пути величины (кроме весов , для которых рассчитывается частная производная ). Кроме того, там, где дуги сходятся к одной вершине, нужно выполнить сложение произведений, полученных на этих дугах.

Рис. 2.  Сеть обратного распространения ошибки

Так, например, чтобы посчитать производную , нужно перемножить величины , а для вычисления производной нужно посчитать произведения

и

а затем сложить эти произведения и результат умножить на и . Таким образом, получим

Итак, метод обратного распространения — способ быстрого расчета градиента функции ошибки. Расчет производится от выходного слоя к входному по рекуррентным формулам и не требует пересчета выходных значений нейронов. Обратное распространение ошибки позволяет во много раз сократить вычислительные затраты на расчет градиента по сравнению с расчетом по определению градиента. Зная градиент, можно применить множество методов теории оптимизации, использующих первую производную. Быстрый расчет градиента необходим во многих методах оптимизации (обучения), поэтому значение алгоритма обратного распространения в теории нейросетей велико.