- •Лекция 5 Алгоритмы вычисления определенных интегралов.
- •Метод прямоугольников.
- •Формулы Ньютона-Котеса
- •Формула трапеций.
- •Формула парабол (Симпсона)
- •Алгоритм вычисления суммы бесконечного ряда
- •Алгоритмы нахождения корней уравнений.
- •Метод половинного деления
- •Метод касательных
- •Алгоритмы обработки массивов
- •Алгоритм обработка записей
Алгоритмы нахождения корней уравнений.
Решение алгебраических уравнений численными методами состоит из двух этапов:
– отделение корней, т. е. отыскание достаточно малых интервалов (a,b), в каждом из которых заключен один и только один корень;
– вычисление (уточнение) корняс заданной погрешностью.
Рассмотрим более подробно алгоритмы для уточнения корней.
Метод половинного деления
Метод половинного
деленияявляется более универсальным,
всегда приводит к искомому результату,
хотя и требует большого объема вычислений.
Для нахождения корня уравненияf(x)=0,
принадлежащего отрезку [a,
b], делим отрезок
пополамz = (a+b)/2
(см. рис. 5.12,а). Далее рассмотрим значения
функцииy =f(x)
в точкахx =aиx =z.
Если значенияf(a)
иf(z)
разных знаков, т. е.f(a)
f(z)
< 0, то исходный отрезок [a,
b] уменьшим в два
раза путем переноса точкиx=b в точкуx
= z. Новый отрезок
[a, b]
вновь делим пополам (см. рис. 5.12,б) и так
какf(a)
f(z)
< 0, то переносим точкуx
=aв точкуx
=z, уменьшая [a,
b] в два раза. Повторяем
указанную процедуру до тех пор, пока
длина отрезка, содержащего корень, не
станет меньше заданной погрешности ε.
Любое значение![]() является искомым значением корня, однако
на практике в качестве корня выбирают
середину отрезка, т. е.x
= (a+b)/2.
является искомым значением корня, однако
на практике в качестве корня выбирают
середину отрезка, т. е.x
= (a+b)/2.
При организации итерационного цикла вычисляется последовательность отрезков
[a0,b0], [a1,b1], …, [an,bn], … ,
для которой
![]()
Для контроля точности вычисления корня можно использовать следующую последовательность значений
![]()
поэтому условие выхода из цикла
![]()
или условие продолжения цикла
![]()
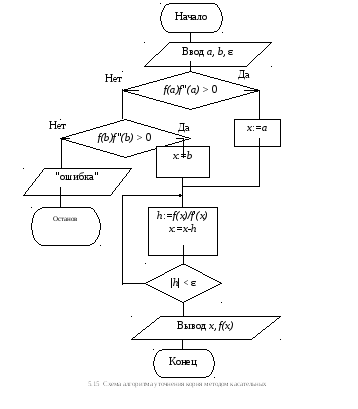
С хема
алгоритма уточнения корня алгебраического
уравнения методом половинного деления
приведена на рис. 5.13. В результате
выполнения такого алгоритма выводится
значение корня (с заданной погрешностью),
а также значение функцииf(x),
которое очень близко к нулевому значению
и может быть использовано для контроля
правильности полученного результата.
хема
алгоритма уточнения корня алгебраического
уравнения методом половинного деления
приведена на рис. 5.13. В результате
выполнения такого алгоритма выводится
значение корня (с заданной погрешностью),
а также значение функцииf(x),
которое очень близко к нулевому значению
и может быть использовано для контроля
правильности полученного результата.

 y
y
f(z)
a
x* z b
f(a)
a)
y
y=f(x)
0 a x*
f(z) z b x
f(a)
b)
Рис.
5.12 Графическая иллюстрация
метода половинного
деления
Метод касательных
Для обеспечения сходимости метода касательных(метода Ньютона) необходимо, чтобы производныеf' (x) и f" (x) были определены, непрерывны и сохраняли постоянные знаки на отрезке [a, b]. На рис. 5.14 представлена геометрическая интерпретация метода Ньютона.
Выберем некоторую точку x0на отрезке [a, b] и проведем касательную к кривойy=f(x) в точкеP0(x0,y0). Ее уравнение
y=y0+f' (x0)(x–x0),
где y0=f(x0).
Новое приближение корня х1, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.
![]()
y
y0
y1
y2
Выберем некоторую точку x0на отрезке [a, b] и проведем касательную к кривойy=f(x) в точкеP0(x0,y0). Ее уравнение
y=y0+f' (x0)(x–x0),
где y0=f(x0).
Новое приближение корня х1, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.
![]()
Проведя касательную через точку P1(x1,y1), получим второе приближение корняx2. Вычисление приближений корня по формуле
![]()
продолжается до выполнения неравенства
![]() ,
,
где ε – абсолютная погрешность определения корня уравнения.
Начальное приближение х0 выбирают таким образом, чтобы выполнялось условие
![]()
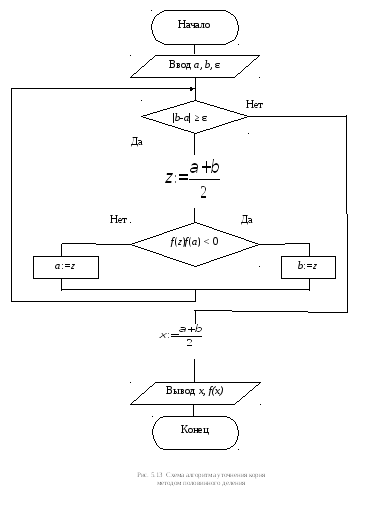
В противном случае сходимость метода Ньютона не гарантируется. На практике выбирают x0=a илиx0=b, в зависимости от того, в какой из этих точек выполняется указанное условие. Схема алгоритма уточнения корня методом Ньютона (методом касательных) приведена на рис. 5.15.