2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 8 (1)

y	0	=	f	0		(u, y, t) = G[u, y, t];
y		=	f		(u, y, t);
1			1
. . . . . . . . . .
y	n	=	f	n		(u, y, t),

или в общем виде

yn = fi (u, y, t)

(i

=

0, ...,

n)

.

(8.39)

Важную переменные ψ

роль в

0	(t), ,

принципе максимума играют вспомогательные ψn ((t) и функция

H

n

= ψi (t) fi (u, i =0

y,

t)

.

(8.40)

Функции

Важно

определением

ψi (t) определяются из дифференциальных уравнений
dψi dt = −H yi	(i = 0, ..., n)	.	(8.41)
подчеркнуть, что уравнение (8.41)			является
функций ψi (t) , и на	вопрос «Что такое		функции

ψ	(t)
i

?» исчерпывающим

ответом будет: «Это функции, которые

удовлетворяют уравнению (8.41)».

H	из (8.40), то получим
	dψ	i		n		f	k
			= −		ψk (t)
	dt
			k	=0

Если в (8.41) подставить функцию

(u,	y, t)	(i = 0, ..., n) .	(8.42)
y
i

Это равенство можно использовать как иную формулировку определения функций ψi (t) .

Кстати, из (8.39) и (8.40) следует, что

dy	dt = H ψ		i	(i = 0,
i
Действительно, так как		H ψi =

..., fi ,

n

) .

то

(8.43)

уравнения (8.43)

эквивалентны уравнениям (8.39).

Если уравнения (8.43) и (8.41) записать совместно dψi dt = − H yi ;

dyi dt = H ψi ,

то можно заметить определенную симметрию в этой системе уравнений. Уравнения такого вида называют канонически сопряженными.

Теперь сформулируем основную теорему рассматриваемого метода (принцип максимума):

213

для оптимальности управления		u(t)	и	траектории			y(t)	с
координатами соответственно	u1	(t), ..., ur		(t)	и	y1(t), ..., yr		(t)

необходимо существование такой ненулевой непрерывной функции

ψi (t)	с координатами ψ0		(t), ..., ψn (t), соответствующей функциям
u(t)	и y(t) в силу уравнений (8.42), что при любом t				(t0	t T )
функция		H [ψ(t), y(t), u]	переменного	u достигает	в	точке
u = u(t) максимума:
		H [ψ(t), y(t), u] = max		u .

Рассмотрим максимума его воздействием u(t

)

отличительную особенность вывода принципа авторами. Ограничимся одним управляющим

.

Как и экстремали

при

u(t)

выводе уравнения Эйлера, добавляется вариация

к

η(t)

предполагаемой

,вычисляется

соответствующая первая вариация функционала

δQ

и из равенства

этой вариации нулю выводятся необходимые условия оптимальности u(t) . Характерна форма вариации при выводе принципа максимума

(рис. 8.8). Это импульс в момент τ бесконечно малой длительности ε , но конечной, произвольной высоты u(τ) . Единственное условие,

которое наложено на величину

u(τ)

, – это требования ограничения

u(τ)

. Например, если

u

1

,

то −1 u(τ) +1. Вариация такого

вида названа игольчатой вариацией.

Рис. 8.8

Важно отметить, что игольчатая вариация существенно отличается от вариаций, с помощью которых выводится уравнение

214

Эйлера. Последние должны были представлять собой гладкие функции, в то время как игольчатая вариация является «скачкообразной». Использование скачкообразных вариаций позволяет включить в класс отыскиваемых экстремалей кусочнонепрерывные функции. А между тем, именно кусочно-непрерывные функции являются экстремалями во многих задачах оптимального управления, как это мы увидим из последующих примеров.

Прежде чем перейти к примерам, наметим план решения задачи

спомощью принципа максимума.

1.Записываем уравнения объекта в виде системы уравнений первого порядка (8.39), не забыв уравнения для функционала (8.38):

yi = fi (u,

2. Составляем функцию H

y, t)

:

(i

=

0, ...,

n)

.

H

n

= ψi (t) fi (u, i =0

y,

t)

.

3. Определяем значение

H

u =

, максимизирующее функцию

max	u	, ..., u	.
			r
	1

H

:

(8.44)

4. Составляем уравнения (8.41) для определения ψi (t) :

dψi	dt = −H yi (i = 0, ..., n) .
Через функции	ψi (t)	выражается искомое		оптимальное
управление.
Особенностью принципа максимума является то, что
вариационная задача нахождения функции			u(t)	доставляющей
экстремум функционалу	Q , заменена гораздо более простой задачей

математического анализа – задачей нахождения параметра u ,

доставляющего максимум вспомогательной функции	H (u) . Отсюда
понятно и название метода – принцип максимума.

Пример 8.1. Решим с помощью принципа максимума задачу 8.1 об оптимальном по быстродействию управлении объектом с уравнением y = u при ограничении на управление u 1.

Решение. Составим систему уравнений первого порядка,

описывающих объект, вводя обозначения		1		;		2	= y	:
		y	= y		y
y1 = y2 ,	y2 = u .							(8.45)

215

Функционалом является длительность процесса

Q = T

=

T 1dt

0

,

поэтому дифференциальное уравнение для функционала вид

y0 =1.

(8.38) имеет

(8.46)

Добавляя (8.46) к (8.45), получим полную исходную систему уравнений объекта

y	0	= 1;
y		= y	2	;
1
y	2	= u.

Составляем функцию

H

:

2

H = ψi fi i =0

= ψ	0	1+ ψ y	2
		1

+ ψ	u
2

.

(8.47)

В (8.47) только последнее слагаемое

можно обеспечить максимальное значение				H
этого слагаемого, т.е. необходимо, чтобы
ψ	2	(t)u = max	u 1	.

зависит от , добившись

u , поэтому максимума

(8.48)

Значения u, максимизирующие (8.48), следует брать на

границах, т. е.

u = +1 или u = −1. Очевидно, что при

ψ

2

(t) 0

следует

брать

u = +1,

а при

ψ

2

(t) 0

необходимо

u = −1.

Этот закон

управления можно записать с помощью функции sign :

u = sign	2	(t)	.

Для определения функций ψi (t) составим

уравнения типа (8.41):

dψ0 dt = − H y0 = 0; dψ1 dt = − H y1 = 0; dψ2 dt = − H y2 = −ψi .

(8.49)

дифференциальные

Решения этих уравнений имеют вид

ψ	0	= const = C	0	;

ψ	1	= const = C			;
				1
ψ	2	= C	2	− C t.
				1

Подставляя (8.50) в (8.49), получим окончательно u = sign C2 − C1t) .

(8.50)

(8.51)

216

Так как функция

ψ	2	= C	2	− C t
				1

может менять знак не более

одного раза, то оптимальное управление (8.51) представляет собой кусочно-постоянную функцию, принимающую предельные значения

+ 1

или −1

и имеющую не более двух интервалов постоянства.

Такое же решение было получено в разделе 8.3 при синтезе оптимальной системы.

На основе рассмотренного примера можно заметить, что

функцию	y0 = f0 , а			следовательно, ψ0 (t)	можно	не	включать в
выражение		для	H ,	если функционал не	содержит	в	явном виде
управления		u ,	так как в этом случае слагаемое ψ0 f0				не влияет на

максимизацию

H

.

Пример 8.2. Рассмотрим задачу 8.6 об оптимальной по быстродействию встрече двух движущихся объектов. Закон сближения объектов описывается уравнением второго порядка (8.23) T x + x = u − b с начальными условиями (8.24), которые записываются

x(0) = −a;

x(0) =

−b

. Здесь

T

– постоянная времени управляемого

объекта;

b

– скорость движения неуправляемого объекта;

a

–

начальное рассогласование между объектами. Все три величины:

T

,

b , a – заданные постоянные числа.

Решение. Поскольку функционалом является время процесса, то

уравнение

x0

= f0 не включается в число уравнений задачи.

Запишем систему

уравнений типа (8.39), обозначив

1

2

= x

:

x = x;

x

x

= x

2

;

1

(8.52)

x

= (1/ T )(−x

+ u − b).

2

2

Составим функцию

H

:

2

H =

ψ

i

f

i

= ψ x

2

+ ψ

2

(1/ T )(−x

2

+ u − b) =

1

i =1

= ψ1x2 −

1

ψ2 x2

+

b

ψ2u −

b

ψ2.

(8.53)

T

T

T

От управления u

в (8.53)

зависит только последнее слагаемое,

поэтому H = max |u| 1,

когда

1

ψ2u = max |u| 1 , откуда

получаем

T

очевидный закон управления

u = sign [ψ2 (t)].

(8.54)

217

Составим дифференциальные уравнения для функций

dψ	/ dt = − H / x	= 0;
1	1

ψ	(t)
i

:

dψ	2	/ dt = − H / x	2	= −ψ	+ (1/ T )ψ	2	.
				1
Из первого уравнения следует
		ψ1 = const ,					(8.55)

а из второго с учетом (8.55)

ψ	2	(t) = C +
		1

Подставляя (8.56) в (8.54), оптимального управления

C2e	t / T	.	(8.56)
запишем			окончательно закон

u = sign (C1 + C2e	t / T	) .

На рис. 8.9 показаны графики функции сочетаний постоянных интегрирования: кривая

кривая 2 – для						1				,		2		; кривая 3 – для			1
– для	1		,		C			0			C		0			C
						2			. Как видно, функция							2
	C	0		C			0								ψ		(t)

	2								(8.57)
ψ		(t)		для различных
1 для					C	0		,	C	2	0	;
					1
0		,	C	2		0	и кривая 4

не более одного раза

меняет знак, следовательно, оптимальное управление содержит не более двух интервалов постоянства.

Рис. 8.9

Рис. 8.10

Из физического смысла задачи (см. траектории объектов A и B на рис. 8.4, а ясно, что вначале управление должно обеспечить разгон объекта B , а затем его торможение. С учетом результата (8.57) и физического смысла задачи можно утверждать, что управление

должно состоять		из	двух интервалов (рис. 8.10): на первом для
0 t t1	u = +1,	а	на	втором для	t1 t t2 управление u = −1.
Моменты	переключения			ti и окончания процесса сближения		t2
составляют неизвестные				параметры	закона управления. Для	t t2

218

движение объектов будет проходить одинаково, если положить u = b.

При этом, как следует из закона сближения объектов (8.23),

x = x = 0 .

Определим	t1 и t2	, используя уравнения системы и граничные
условия. Принимая за единицу времени постоянную T , т. е. вводя
нормированное	время	= t / T , перепишем	дифференциальное
уравнение (8.23) закона сближения
		dx2 / d + x2 = u − b .	(8.58)

Граничные условия примут вид

x1(0) = −a;			x1(τ2 ) = 0;					x2 (0) = −b;
Подставляя для			отрезка		времени				[0, τ1]
(8.58), имеем
			x	2	+ x	2	= 1 − b		,
откуда
x		= (1 − b) + Ce						−τ	(0 τ
	2

x2 (τ2 ) = 0 .

управление

τ1) .

(8.59) u = +1 в

(8.60)

Постоянную C

интегрирования найдем из начального условия

x2

= −b . Подставляя в (8.60)

τ = 0

, получим

C = −1, а закон изменения

x2

(τ) можно записать в виде

x2 = (1 − b) − e

−τ

(0 τ

τ1) .

(8.61)

Интегрируя

условий

(8.86), с учетом

начальных»

1

определим закон изменения

1

на отрезке

1

:

x (0) = −a

x

(τ)

[0, τ ]

x1

(τ) = −(a +1) + (1 − b) + e

−τ

(0 τ τ1) .

(8.62)

Подставляя в уравнения (8.61) и

(8.62)

τ = τ

вычислим

1 ,

значения x

(τ )

и x

2

(τ

2

) , являющиеся начальными условиями для

1

1

дифференциального

уравнения

движения

на

втором

интервале

τ

τ τ

2 , где u

= −1:

1

x (τ ) = −(a +1) + (1 − b) + e−τ ;

1

1

1

(8.63)

(τ ) = (1 − b) − e−τ .

x

2

1

Запишем уравнение движения для τ1 τ τ2 :

(8.64)

x

2

+ x

2

= −(1 + b)

.

Интегрируя (8.64) с учетом начальных условий (8.63), получим

x2 (τ) = −(1 + b) +

(2 − e

−τ

1

)e

−(τ-τ

)

τ1 τ τ2.

(8.65)

1

Закон изменения x1(τ1)

для отрезка времени τ1 τ τ2 найдем,

проинтегрировав (8.65) с учетом начальных условий (8.63)

219

x	(τ	2
1

x1 По ) =

(τ) = (1 − a + условию

x2 (τ2 ) = 0 ,

2τ1) − (1 + b)τ − (2 − e	−τ	1	)e	−(τ-τ	)	τ1	τ τ2.	(8.66)
				1
задачи в момент окончания процесса
поэтому, подставляя			в	(8.65) и			(8.66)	τ = τ2

получим систему уравнений для определения моментов времени

τ2

:

− (1 + b) + (2 − e	−τ		)e	−(τ		-τ	)	= 0;
		1			2	1

τ1

и

(1 − a + 2τ	) − (1 + b)τ		− (2 − e	−τ	1 )e	−(τ		-τ	)	= 0.
		2					2	1
1

Путем несложных преобразований от этой системы уравнений можно перейти к другой более простой паре уравнений

τ2

=

2τ

− a − b

2 − e

−τ

1

τ2

=

1

;

τ2 = τ1 + ln

.

1 + b

1 + b

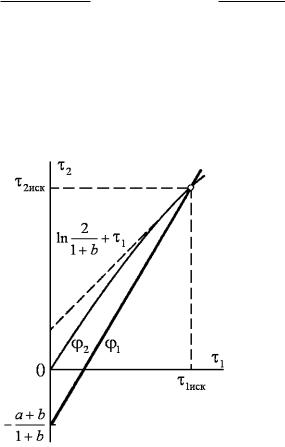
Рассматривая

эти

уравнения

как функции

вида

τ

2

=

2

1

, можно построить на плоскости с координатами

(τ

)

(8.67)

1		1		и
	(τ		)
τ1		и		τ2

соответствующие графики (рис. 8.11), определяет искомые моменты времени

точка пересечения которых и

τ1иск и τ2иск .

Рис. 8.11

8.6.Контрольные вопросы

1.Какую функцию называют кусочно-непрерывной?

2.Какие функции называют функционалами, а какие экстремалями?

220

3.Какие примеры постановки оптимального управления вы

знаете?

4.Какой вид имеет функционал при оптимальном быстродействии?

5.Что необходимо для реализации оптимального процесса в разомкнутой системе?

6.Что вы знаете о методе динамического программирования?

7.Назовите четыре основных метода в вариационном исчислении, используемых для решения задач оптимального управления?

8.Сформулируйте основную теорему принципа максимума.

9.Назовите план решения задачи с помощью принципа максимума.

10.Особенности применения принципа максимума.

221