Введение в современную теорию поляризации радиолокационных сигналов. Том 1. Поляризация плоских электромагнитных волн и её преобразования

1 T / 2

T / 2

ET

t

ET

t

2

exp

j

t

t

2

dt dt

2

,

(2.47б)

T

Y

1

Y

1

1

T / 2

T / 2

а их взаимная мощность определяется как

GT

1

ST

ST

XY

T

X

Y

1 T / 2

T / 2

ET

t

ET

t

2

exp

j

t

t

2

dt dt

2

,

(2.47в)

T

X

1

Y

1

1

T / 2

T / 2

GT

1

ST

ST

YX

T

Y

X

1 T / 2

T / 2

ET

t

ET

t

2

exp

j

t

t

2

dt dt

2

.

(2.47г)

T

Y

1

X

1

1

T / 2

T / 2

Совокупность реализаций G

не стремится к определенному пределу даже

при T

, а является случайной функцией. Усредним выражения (2.47) и

запишем результаты усреднения в виде

FT

1 T / 2

T / 2

,

(2.48а)

G

X

B

t ,t

2

exp

i

t

t

2

dt dt

2

XX

T T / 2

XX

1

1

1

T / 2

FT

1 T / 2

T / 2

,

(2.48б)

G

B

t ,t

2

exp

i

t

t

2

dt dt

2

YY

Y

T T / 2

YY

1

1

1

T / 2

FT

G

1

T / 2

T / 2

B

t ,t

exp

i

t

t

dt dt

,

(2.48в)

XY

XY

2

2

2

XY

T

1

1

1

T / 2

T / 2

FT

G

1

T / 2

T / 2

B

t ,t

exp

i

t

t

dt dt

.

(2.48г)

2

2

2

YX

YX

T

YX

1

1

1

T / 2

T / 2

Здесь

BXX

t1 ,t2

EX

t1

EX

t2

,

(2.49а)

BYY

t1 ,t2

EY

t1

EY

t2

(2.49б)

есть

автокорреляционные

функции

поляризационно-ортогональных

составляющих EX (t) и EY (t) , а

BXY

t1 ,t2

EX

t1

EY

t2

,

(2.49в)

121

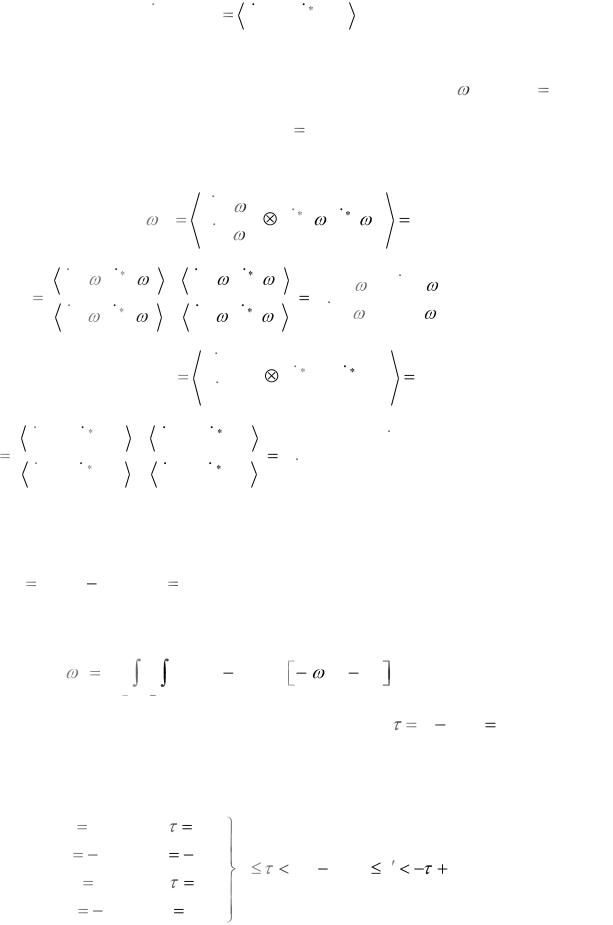
BYX

t1 ,t2

EY t1 EX

t2

(2.49г)

есть их взаимно-корреляционные функции.

Нетрудно

видеть,

что

спектральные

функции

FT

( j,l x, y )и

jl

корреляционные функции Bjl

t1 ,t2

( j,l

x, y ) представляют собой элементы

матриц, определенных с использованием правил (2.27):

FT

SX ( )

S

X

( )S ( )

jl

SY (

)

Y

SX ( )SX ( )

SX ( )SY ( )

T

)

T

(

)

FXX (

FXY

,

(2.50)

S (

)S

(

)

S ( )S (

)

FYXT (

)

FYYT (

)

Y

X

Y

Y

Bjl t1 ,t2

EX (t1 )

EX

(t2 )EY

(t2 )

EY (t1 )

EX (t1 )EX (t2 )

EX

(t1 )EY (t2 )

B

XX

t ,t

2

B

XY

t ,t

2

1

1

.

(2.51)

BYX t1 ,t2

BYY t1 ,t2

E (t )E

(t

)

E (t )E (t

)

Y

1

X

2

Y

1

Y

2

Элементы матриц (2.50) и (2.51) связаны интегральными преобразованиями

(2.48).

Для

стационарных

и

стационарно

связанных

процессов

Bjl t1,t2

Bjl t1

t2 ,

j,l x, y .

Перепишем выражения (2.48) в унифицированном виде

2 T / 2

T / 2

FT

BT

t

t

2

exp i t

t

2

dt dt

2

(2.52)

jl

jl

1

1

1

T T / 2 T / 2

и произведем в выражении (2.52) замену переменных

t1 t2 ;t2

t2 . При этом

связь между старыми и новыми пределами интегрирования определяется соотношениями:

t1	T / 2,		T
t2	T / 2,	t2	T / 2	0	T ;( T / 2) t	(T / 2) ,
t1	T / 2,		0
t2	T / 2,	t2	T / 2
					122

t1	T / 2,		T
t2	T / 2,	t2	T / 2	T	0;(	T / 2) t (T / 2)
t1	T / 2,		0
t2	T / 2,	t2	T / 2

В результате замены переменных интегрирование по квадрату переходит в интегрирование по параллелограмму (рисунок 2.1). Выражение (2.52) в новых пределах приобретает вид

FT

2 T / 2 (

T / 2)

B

exp j

dt

d

jl

jl

T

2

0

T / 2

2 0

T / 2

2

T

Bjl

exp

j

dt2 d

T

Bjl (

) exp

j

d

T T

T

T / 2

0

2

0

T

T

Bjl (

) exp

j

d

2

1

Bjl

exp j

d .

(2.53) В

T

T

T

T

/ T

0 и предел выражения (2.53) принимает вид

случае T

величина

F

jl

lim FT

2

B

jl

exp

j

d ,

j,l

x, y .

(2.54)

T

jl

Интеграл (2.54) существует, если корреляционная функция Bjl

абсолютно

интегрируема, что для стационарного

jl Bjl (0) всегда имеет место.

t1

1	0.5T

процесса с конечной дисперсией

2

t2

0.5T		0.5T
4	0.5T	3
1		T

4	2 t2
0.5T	123
	0.5T

Рис.2.1

Выражения (2.54) для случаев j l x и j l y дают энергетический спектр

поляризационно-ортогональных составляющих EX (t) и EY (t) . Этот спектр представляет собой усредненную картину распределения энергии процесса по частотам гармонических составляющих, но не учитывает их фазовой структуры. Энергетические спектры FXX ( ) и FYY ( ) представляют собой действительные функции.

Для случаев j x;l y , и j y;l x , выражения (2.54) дают взаимный

энергетический спектр поляризационно-ортогональных составляющих EX (t) и

EY (t) (или «энергию связи» этих составляющих). Взаимный энергетический спектр представляет собой комплексную функцию. Прямое преобразование Фурье (2.54) и обратное преобразование Фурье

	Bjl	1		Fjl	( )exp j d , ( j,l x, y)	(2.55)
		2
	в совокупности	составляют			теорему Винера-Хинчина [17,34] в приложении к
	частично поляризованным волнам.

В заключение подраздела отметим, что (2х2) матрица когерентности для совпадающих моментов времени, введенная соотношением (2.27) является

частным случаем соотношения		(2.55).		Поскольку	t1 t2 , то для случая
совпадающих моментов времени			0 и выражение (2.55) принимает вид
Bjl 0		1	Fjl	( )d .	(2.56)
2
			124

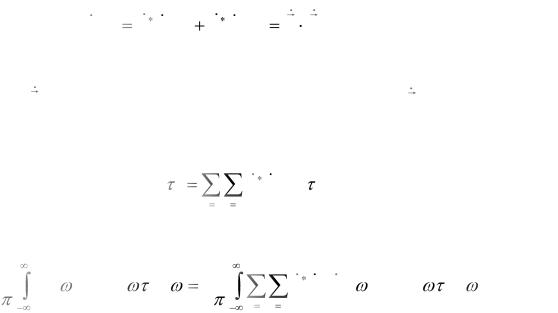
Соотношение (2.56) есть не что иное, как одно из возможных представлений

теоремы Парсеваля.

2.4 Общая форма (2х2) матрицы когерентности и ее использование для

разложения закона интерференции.

Ряд свойств (2х2) матрицы когерентности, такие как эрмитовость и неотрицательная определенность были просто постулированы в подразделе

(2.2), а разложение МК на суммы МК, отвечающих абсолютно неполяризованной волне и полностью поляризованной волне было проделано на физическом уровне строгости. Однако все эти понятия должны быть обоснованы и доказаны. Это обоснование будет проведено с использованием

результатов [8].

Будем полагать, что, за исключением отдельных, особо указанных случаев,

рассматривается матрица когерентности квазимонохроматического поля

Bjl (0) , определенная в совпадающие моменты времени выражениями (2.27)

или (2.56).
Тот факт, что (2х2) матрица когерентности							представляет собой
				Bjl (0)
неотрицательно определенную	матрицу,	докажем,					вводя линейную
комбинацию вида
Y t S1 E1 (t)	S2 E2 (t) S	E(t) ,					(2.57)

представляющую собой скалярное произведение некоторого комплексного

вектора S				и комплексного				вектора Джонса E1 (t) .				Определим
автокорреляционную функцию этой комбинации как
						2		2
					BY ( )			S j Sl Bjl (		) .		(2.58)
						j	1 l 1
Записывая выражение (2.58) в спектральной форме, получим
1						1		2	2
		BY	(	)exp j	d				S j	S jl Fjl ( )exp j	d	, (2.59)
2						2
								j 1 l	1
								125

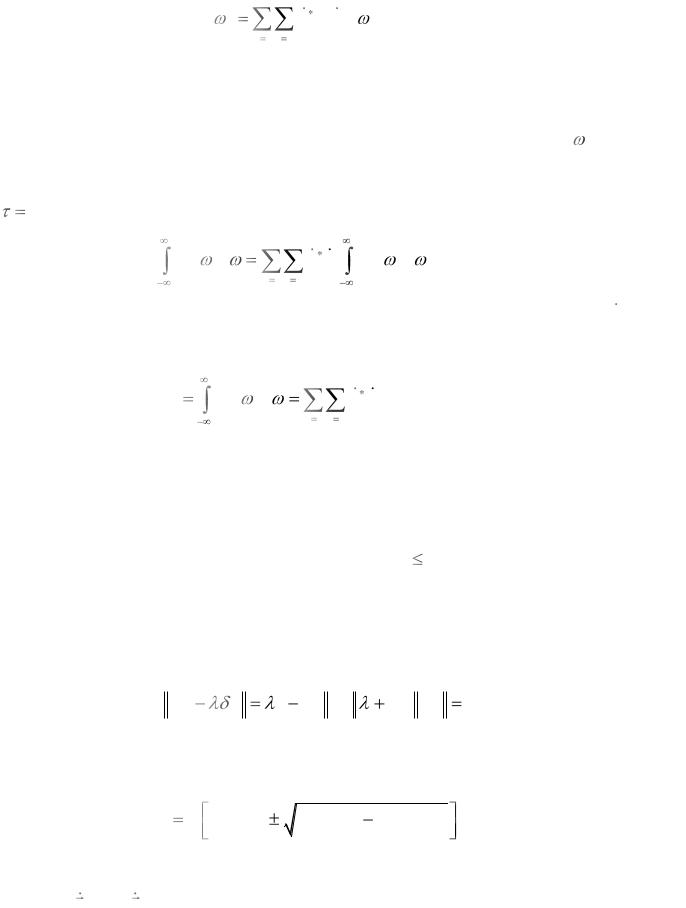
где энергетический спектр

2	2
BY	S j Sl Fjl ( )	(2.60)
j	1 l 1

есть действительная неотрицательная функция по определению. Отсюда следует, что квадратичная форма в правой части выражения (2.60) представляет собой неотрицательно определенную эрмитову форму. Матрица Fjl ( ) этой формы также эрмитова и неотрицательно определенная. Используя условие

0 применительно к выражению (2.59), получим

2	2
BY ( )d	S j Sl Fjl ( )d ,
j	1 l 1

откуда, с учетом выражения (2.56), следует , что дисперсия процесса Y (t)

определяется величиной

	2	2
G2	B ( )d	S	j	S	B	jl	(0) .		(2.61)
Y	Y			l
	j 1	j 1
Выражение (2.61) показывает, что матрица когерентности									Bjl (0)		, найденная

для совпадающих моментов времени, представляет собой эрмитову,

неотрицательно определенную матрицу. В		связи			с этим ранг матрицы
когерентности частично-поляризованной волны		R 2 .
Предположим, что исследуемая (2х2) матрица		Bjl (0)			невырождена (т.е. имеет

не равный нулю детерминант). Тогда для определения ее собственных значений можно записать вековое уравнение

det Bjl		2	Sp Bjl	det Bjl 0 ,	(2.62)
	jl

корни которого (собственные значения матрицы когерентности) определяются выражением

1

A

Sp

B

jl

Sp2

B

jl

4 det

B

jl

.

(2.63)

1,2

2

Собственным значениям

A1 и A2

отвечают два (в общем случае комплексных)

вектора m(1) и n(1) .

Поскольку собственные векторы матрицы когерентности

126

Bjl (0) образуют ее собственный базис, то вектор Джонса анализируемой волны

E(t)		E1 (t)
		E2 (t)
может быть представлен разложением по направлениям этих векторов:

E(t) E (t)m(1)	E (t)n(1) .	(2.64)
m	n

2

2

Здесь

E (t)

E

j

(t)m(1)

;

E (t)

E

j

(t)n(1)

-

скалярные произведения

m

j

n

j

j 1

j 1

вектора E(t)

с каждым из собственных векторов

m(1)

и n(1) . Вводя нормировку

собственных векторов

2

2

m(1)j m(1)j

n(1)j n(1)j

1,

j 1

j 1

получим

Em (t) 2

En (t) 2

2

2

2

2

E

(t)m(1)

E (t)m(1)

B

jl

m(1)

j

j

l

l

j

j 1 l 1

j 1 l 1

2

2

2

2

E

(t)n(1)

E (t)n(1)

B

jl

n(1)

j

j

l

l

j

j

1 l 1

j

1 l 1

2

2

E

(t)m(1)

E (t)n(1)

0,

j

j

l

l

j 1 l

1

поскольку, по определению собственных векторов m(1)

ml(1) A1 ; (2.65а)

nl(1) A2 ; (2.65б)

(2.65в)

и n(1) ,

2

2

B

jl

(t)m(1)

A m(1) ;

B

jl

(t)n(1)

A n(1) .

(2.65г)

j

1

l

j

2 l

j 1

j

1

Вводя обозначения

m

A m(1) , n

A n(1)

,

найдем

элементы матрицы

1

2

когерентности по обычному правилу

Bjl

E j (t)El (t) .

(2.66)

Учитывая выражения (2.64) и (2.65),

запишем матрицу когерентности (2.66) в

виде

127

Bjl

mj ml

nj nl

.

(2.67)

Поскольку векторы m /

m

; n /

n

образуют

ортонормированную пару, то

выполняется условие

mj ml

n j nl

jl .

(2.68)

m2

n2

Используя соотношение (2.68), исключим из выражения (2.67) слагаемое nj nl :

B

jl

n2

jl

(1

n2

)

m m

,

(2.69)

m2

j l

Учитывая затем, что m2

A ; n2

A

,

получим окончательно

1

2

Bjl

A2

(1

A2 / A1 )

mj ml

( j,l 1, 2) .

(2.70)

jl

Выражение (2.70), представляющее собой сумму двух независимых матриц

когерентности A2 jl и (1 A2 / A1 ) mj ml , назовем общей формой (2х2)

матрицы когерентности частично поляризованной волны. При этом исходный комплексный вектор E(t) может быть представлен суммой двух независимых комплексных векторов

E(t)

E 1 t

E 2

t

,

(2.71)

которым соответствуют матрицы когерентности

B 1

A

и

B 2

(1 A / A )

m m

.

jl

jl

2

jl

2

1

j l

Рассмотрим теперь свойства матричных слагаемых в общей форме (2.70).

Первое слагаемых этой формы представляет собой изотропный тензор. Оно не содержит никакого другого вектора или тензора, с которым можно было бы связать выделение некоторого преимущественного направления ориентации составляющей E(1) t суммарного комплексного вектора. Отсюда следует

вывод, что составляющая E(1) t характеризует статистически изотропную

128

часть исследуемого комплексного вектора E t . Подтвердим этот факт

анализом общей формы матрицы когерентности двумерного изотропного поля.

Пусть имеется некоторое двумерное изотропное случайное поле,

описываемое комплексным

вектором

I . Зададим два произвольных

комплексных вектора S, R , и рассмотрим корреляцию проекций комплексного

вектора I на направления векторов S, R :

2

2

N

S I *

R* I

S

R* N

jl

,

(2.72)

j l

j

1 l 1

где величины N jl представляют собой элементы

матриц когерентности

N jl

поля, характеризуемого комплексным вектором I .

Повернем систему векторов

S, R как жесткое целое на произвольный угол в

плоскости векторам I . При этом взаимная ориентация S

и R не изменяется,

что приводит к сохранению их скалярного произведения. В случае

статистической изотропии поля вектора I величина N при поворотах не

изменяется. Таким образом, требование инвариантности выражения (2.72)

относительно поворотов системы векторов S и R является определяющим

для статистически изотропного векторного поля [79]. Так как при повороте

сохраняется лишь скалярное произведение S R*		S j R*j , величина N может
зависеть только от этого произведения:
2	2
	S j R*l N jl N (S R* ) .	(2.73)
j	1 l 1

Поскольку левая часть выражения (2.72) линейна по компонентам комплексных

векторов S	и R ,	то и правая часть может зависеть от скалярного
	2
произведения	S j R*j	лишь линейно. Следовательно
	j 1

129

2

N (S

R* )

P

S j R*j .

(2.74)

j

1

Правая часть соотношения (2.74) может быть представлена в виде свертки

2

2

2

P

S

j

P*

P

S

R*

jl

.

(2.75)

j

j

l

j

1

j

1 l

1

Сравнивая выражения (2.75) и (2.73)

видим, учитывая соотношения (2.74), что

матрица когерентности изотропного комплексного вектора I имеет вид

N jl

P jl .

(2.76)

Выражение (2.76) подтверждает, что матрица

B 1

A

jl

представляет собой

jl

2

(2х2) матрицу когерентности составляющей

E(1) (t)

суммарного комплексного

вектора E(t) и описывает изотропную составляющую суммарного вектора.

Рассмотрим теперь свойства матрицы

B(2)

. Нетрудно убедиться, что ее

jl

детерминант равен нулю, т. е.

B(2)

- матрица первого ранга. Гаральд Крамер

jl

[36] доказал, что распределение вероятностей некоторого двумерного вектора,

характеризуемого матрицей когерентности первого ранга, вырождено и

сосредоточено на направлении единственного собственного вектора этой матрицы. Данный случай соответствует полностью поляризованной волне

эллиптической поляризации при комплексном собственном векторе или волне с линейной поляризации при действительном собственном векторе.

Отсюда следует, что матрица		B(2)		описывает полностью
		jl

поляризованную составляющую исследуемого вектора E(t) . Физический смысл статистической изотропии и полной поляризованности составляющих комплексного вектора E(t) рассмотрим, используя разложение закона интерференции (2.25) для плоской частично-поляризованной волны, который перепишем здесь для удобства:

I ,	B cos2	B sin2
	11	22
		130