Введение в современную теорию поляризации радиолокационных сигналов. Том 1. Поляризация плоских электромагнитных волн и её преобразования

относительно исходной системы координат, принимает максимально возможное значение, равное степени поляризации частично поляризованной волны.

Систему координат, обладающую указанными качествами, называют первым особым базисом частично-поляризованной волны [5].

2.7.2. Второй особый базис.

В подразделе 2.4 было доказано, что матрица когерентности представляет собой эрмитову, неотрицательно определенную матрицу. В связи с этим для

всякой матрицы когерентности || Bjl || существует унитарное матричное

преобразование	ˆ
	P , такое, что
	ˆ	ˆ			A1	0			(0)	|| ,	(2.130)
	P || Bjl	|| P			0	A2			|| Bjl
где A1 , A2 неотрицательные собственные значения. Преобразование (2.130), как
это неоднократно указывалось					ранее,				есть	не что	иное, как результат

вычисления матрицы когерентности для вектора Джонса E ' t после

некоторого унитарного преобразования, совершаемого над исходным вектором

E t	:
	(0)	||	ˆ	ˆ	ˆ	E t	ˆ	ˆ	ˆ
	|| Bjl		PE(t)	PE t	P E t		P	P	|| B jl || P.
При	этом		можно	считать, что	оператор	ˆ	описывает гипотетическое
						P

устройство (прибор), который исключает корреляционную связь между проекциями исходного вектора Джонса без потерь энергии. Таким образом,

преобразованная матрица	когерентности (2.130) позволяет рассматривать
частично-поляризованную	волну после унитарного преобразовании	ˆ	как
		P

сумму двух ортогонально-поляризованных, некоррелированных волн,

обладающих интенсивностью

151

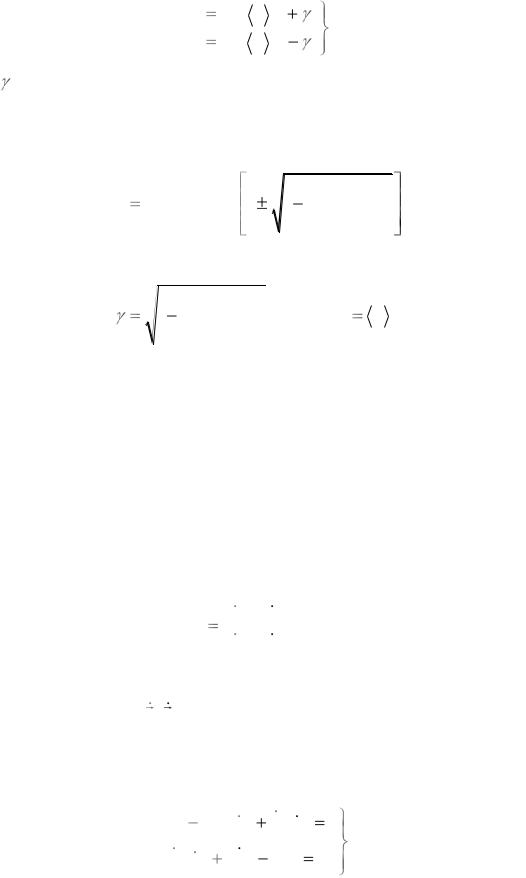
A1	0,5	I	(1	)	,	(2.131)
A2	0,5	I	1

где - степень поляризации волны.

При выводе соотношений (2.131) в выражения для собственных чисел матрицы когерентности

A1/ 2 0,5Sp || Bjl || 1							1	4det || Bjl ||
								Sp2 || B	jl	||
были подставлены величины
1		4 det || Bjl		||	,		Sp || Bjl ||			I .
		Sp2 || B	jl	||

Систему координат, в которой частично-поляризованная волна представлена двумя некоррелированными (некогерентными) компонентами, называют вторым особым базисом матрицы когерентности частично-поляризованной волны [5,9]. Этот базис может эффективно использоваться при построении статистических моделей частично-поляризованных волн.

Столбцы унитарной матрицы			ˆ		преобразования (2.130)	представляют
			P
собой собственные векторы матрицы когерентности || Bjl ||:
ˆ		m1	n1		.	(2.132)
P		m2	n2

Таким образом, для построения матрицы (2.132) необходимо найти

собственные векторы m; n , матрицы || Bjl ||.

Запишем в развернутом виде системы уравнений (2.65г), определяющие собственные векторы матрицы когерентности:

b11 A1 m1	b12 m2	0
		,	(2.133а)
b21m1 b22	A1	0

152

b11 A2 n1 b12 n2 0

. (2.133б)

b21n1

b22 A2 n2 0

Системы однородных уравнений (2.133a,б) могут быть разрешены, поскольку соответствующие определители равны нулю:

1

b

A

b

A

| b

|2

0 ,

11

1

22

1

12

1

b

A

b

A

| b

|2

0 .

11

2

22

2

12

Последнее нетрудно доказать, используя соотношения

b b | b |2

A A

,

b b

A A .

11

22

12

1

2

11

22

1

2

Используя системы уравнений (2.133a,б) образуем два отношения

r1

m2

A1

b11

b21

,

(2.134а)

m1

b12

A1

b22

r2

n2

A2

b11

b21

.

(2.134б)

n1

b12

A2

b22

Из свойства унитарности

ˆ

ˆ

||

||

следует, что

P P

jl

m

2

| m |2

1;| n |2

| n |2

1;

(2.135а)

1

2

1

2

m1*n1 m2*n2 0;n1*m1

n2*m2

0 .

(2.135б)

Использование уравнений (2.135а) совместно с уравнениями (2.134a,б)

позволяет определить модули проекций собственных векторов

| m1

|

1

A1

b22

;

1

| r1

2

2

|

A1

b22

2

| b12 |

| m2 |

| r1 |

| b12

|

;

(2.136)

1

| r1

2

2

|

A1

b22

2

| b12 |

| n1

|

1

A1

b22

;

1

| r2

2

2

|

A1

b22

2

| b12 |

153

Детерминанты матриц || Fjl(1) || и

полной поляризованности волн,

|| Fjl(1) || m

m;|| Fjl(2) || n

| n2

|

| r2 |

| b12

|

.

1 | r2 |

2

A1

b22

2

2

| b12 |

Аргументы проекций собственных векторов определяются с использованием

(2.135б) и (2.134a,б):

arg m1 0;arg m2 arg b12 ;arg n2 0;arg n1 arg b12 . (2.137)

Обозначив arg b12

ˆ

12 , запишем окончательно унитарную матрицу P в виде

A

b

A2

b22

ei 12

1

22

A b

2

| b |2

A b

2

| b |2

ˆ

1

12

12

2

22

12

.

(2.138)

P

| b12 | e

i 12

| b12 |

A b

2

| b |2

A b

2

| b |2

1

22

12

2

22

12

Нетрудно убедиться прямой проверкой, что

матрица (2.138) удовлетворяет

условию

ˆ ˆ

|| .

P P || jl

Форма столбцов матрицы

ˆ

свидетельствует о том,

что собственные

P

векторы m и n матрицы когерентности можно рассматривать как полностью поляризованные волны с ортогональными эллипсами поляризации. В полной поляризованности этих волн нетрудно убедиться, построив их матрицы когерентности на основе использования собственных векторы m и n

n .

|| Fjl(2) || равны нулю, что и свидетельствует о отвечающих собственным векторам матрицы

Bil .

2.8 Степень поляризации суммы некоррелированных потоков излучения.

К сожалению, теорема Стокса для аддитивных потоков излучения не позволяет провести анализ возможного влияния различия в ориентации

154

собственных базисов матриц когерентности слагаемых потоков на степень поляризации суммарной волны. При проведении анализа автоматически предполагается, что ориентация собственных векторов матриц когерентности потоков совпадает. Однако однозначный ответ может быть получен только при проведении анализа в единой системе координат, позволяющей связать собственные базисы суммируемых и суммарного потоков. Такой анализ может быть проведен с использованием методов, развитых выше при получении общей формы матрицы когерентности [8].

Предположим, что заданы две некоррелированные частично-

поляризованные волны с совпадающими волновыми векторами. Каждая из этих волн обладает (2х2) матрицей когерентности ранга R=2. Обозначим матрицы

когерентности слагаемых волн как || B(1)jl || и|| B(2)jl || , а матрицу когерентности

суммарной волны как || Bjl ||.

Комплексные векторы суммируемых и суммарного потоков

определяются как

E 1

E 1

t

E 2

E 2

t

t

1

;

t

1

;

E 1

t

E 2

t

2

2

E 1

E 2

E 1

t

E

2

t

E t

t

t

1

1

E 1

t

E

2

t

1

2

соответственно.

Системы собственных векторов матриц когерентности слагаемых волн примем за базисные системы координат. В общем случае эти координатные системы ориентированы произвольно одна относительно другой.

Примем также условия нормирования базисов в виде

	2			2
		a j1 a j1 *		bj1 bj1 *				1;
	j	1		j 1						(2.139)
2		2			2			2
a 2	a 2 *	b 2	b 2 *	1;	a	j	a*	b	b*	1;
j	j	j	j				j	j	j
j 1		j 1		j	1			j 1

155

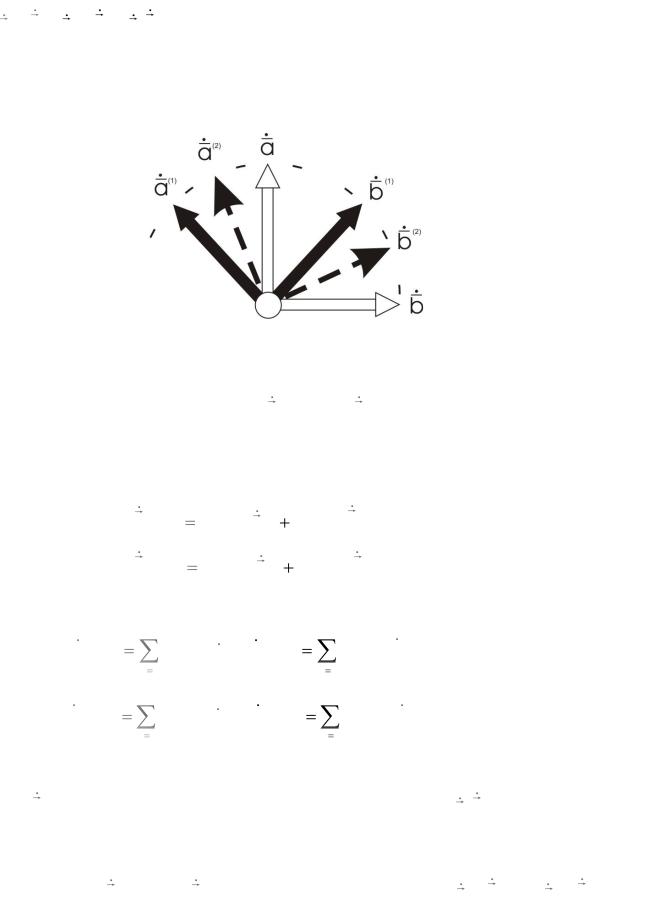
где a 1 ;b 1 ; a 2 ;b 2 ; a;b - системы собственных векторов (в общем случае комплексных) матриц когерентности || B(1)jl ||, || B(2)jl || слагаемых волн и матрицы когерентности || Bjl || суммарной волны соответственно (См. Рис. 2.2).

Рис. 2.2
Представим комплексные векторы E 1 t и E 2	t суммируемых потоков

проекциями на собственные векторы отвечающих этим потокам матриц когерентности:

E 1

t

E 1

t

a 1

E 1

t

b 1

;

(2.140a)

a

b

E 2

t

E 2

t

a 1

E

2

t

b 2

,

(2.140б)

a

b

где

E 1

2

1

1 * ; E 1

2

E 1

t b 1 * ;

t

E

t a

t

a

j

j

b

j

j

j

1

j

1

E 2

2

2

2 * ; E 2

2

2

2 *

t

E

t a

t

E

t b

;

a

j

j

b

j

j

j

1

j

1

Выражения (2.140a,б) позволяют записать комплексный вектор суммарного

потока E t проекциями		на	орты		собственного базиса	a;b его матрицы
когерентности || Bjl ||	с использованием представления комплексных векторов
слагаемых волн E 1 t	и	E 2	t	в собственных базисах		a 1 ,b 1	и a 2 ,b 2
матриц когерентности || B(1)		||, || B(2)		||	этих волн:
	jl		jl
					156

E

t

Ea t

a

Eb

t

b ,

(2.141)

где

2

2

2

2

E t

E 1

t a

1 *

a 1

a*

E

2

t a

2 *

a 2

a*

a

j

j

l

l

j

j

l

l

l 1 j

1

l

1

j

1

2

2

E 1

b 1 *

1 a*

2

2

2

b 2 *

b 2

t

b

E

t

a* ,

(2.142а)

j

l

l

j

j

l

l

l

j

1

l

j

1

2

2

E 1

t a 1 *

a 1 b*

2

2

2

2 * a 2

E t

E

t a

b*

b

j

j

l

l

j

j

l

l

l 1

j

1

l 1 j

1

2

2

E 1

b 1 *

1 b*

2

2

2

b 2 *

b 2

t

b

E

t

b* .

(2.142б)

j

l

l

j

j

l

l

l

j

1

l 1 j

1

Учитывая, что, по определению собственных векторов,

для матриц || Bjl ||,

|| B(1) ||, || B(2) || справедливы соотношения

jl

jl

2

2

Bjl a j

A1 al ;

Bjl bj

A2 bl

,

j

1

j 1

2

1

1

A 1 a 1 ;

2

2

b 1

1 b 1 ,

B

a

B

A

jl

j

1

l

jl

j

2

l

j

1

j 1

2

2

2

A 2

a 2

2

2

2

A 2

b 2

B

a

;

B

b

jl

j

1

l

jl

j

2

l

j

1

j

1

и используя условия нормировки (2.139), видим, что для суммарной волны

| E |2

A ; | E |2

A

,

a

1

b

2

а для слагаемых волн

| E 1

|2

A 1

; | E 1 |2

A 1

a

1

b

2

| E 2

|2

A 2 ,

| E

2

|2

A

2 .

a

1

b

2

Здесь

Ak , i, k

1, 2 - собственные значения матриц когерентности слагаемых

i

волн. Принимая во внимание некоррелированность слагаемых волн, запишем собственные значения A1,2 матрицы когерентности суммарной волны в виде

157

2

2

2

2

| E |2

A A 1

a 1

a*a

1 *a

A 2

a

2 a*a 2 *a

j

a

1

1

l

l

j

j 1

l

l j

l

1

j

1

l

1

j

1

2

2

2

2

A21

bl

1 al*bj1 *a j

A22

bl

2 al*bj

2 *a j ,

(2.143а)

l 1

j

1

l

1

j 1

A A 1

2

2

a 1 b*a 1 b*

A 2

2

2

a 2

b*a 2 *b

| E |2

j

b

2

1

l

l j

j

1

l

l

j

l

1

j

1

l 1

j

1

2

2

2

2

A21

bl

1 bl*bj1 *bj

A22

bl

2 bl*bj

2 *bj .

(2.143б)

l 1

j

1

l

1

j

1

Таким образом, собственные числа матрицы когерентности суммарной волны выражены в виде взвешенных сумм собственных чисел матриц когерентности слагаемых волн. Весовыми коэффициентами являются квадраты скалярных произведений собственных векторов, которые, в соответствии с условиями нормировки (2.139) равны квадратам косинусов углов, определяющим

ориентацию систем собственных векторов a 1 ,b 1 ; a 2 ,b 2 матриц

когерентности слагаемых волн относительно системы собственных векторов a,b матрицы когерентности суммарной волны. Перепишем (2.143) в более

компактном виде

A	A 1	K a	A 2	K a	A 1	K a	A 2	K a ;	(2.144а)
1	1	1	1	2	2	3	2	4
A	A 1	K b	A 2	K b	A 1	K b	A 2	K b .	(2.144б)
2	1	1	1	2	2	3	2	4

Из геометрических соображений и с учетом того, что весовые коэффициенты есть квадраты косинусов, следует

	K a	K b	K ; K a		K b	K	;
	1	3	1	3	1	3		(2.145)
	K a	K b	K	; K a	K b	K	.
	2	4	2	4	2	4

Нетрудно показать, что при любой ориентации систем собственных векторов слагаемых волн относительно системы собственных векторов суммарной волны

выполняются тождества K1		K3	1; K2	K4	1. Отсюда полная мощность
суммарной волны определяется как
		1	1	2		2	,
1	2	1	2	1	2
			158

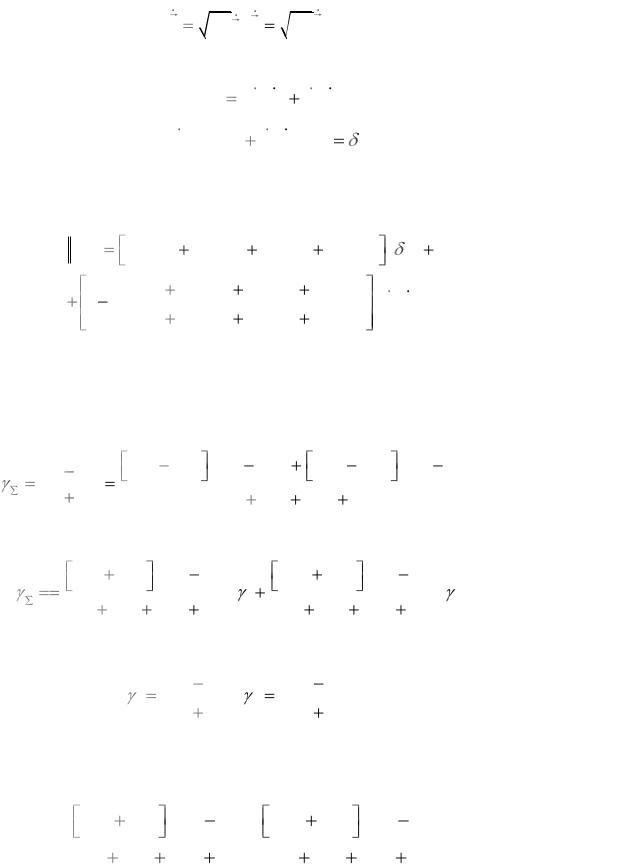
чего и следовало ожидать.

Определим теперь общую форму матрицы когерентности суммарного

потока. Полагая, что A A1 a, B A2 b , в соответствии с методикой построения общей формы матрицы когерентности (см. подраздел 2.4) получим

|| B	jl	|| || A A*		B B* ||.		(2.146)
			j l	j l
Используя соотношение A A* / A2			B B* / B2		jl	и выражения (2.144), (2.145)
j l			j	l

запишем окончательно общую форму матрицы когерентности суммарной волны

B	jl			K	3	A 1		K		4	A 2		K A 1				K		2	A		2				jl
						1					1			1	2					2
						1					2				1					2		.								(2.147)
				K3 A1			K4 A1					K1 A2				K2 A2
																								*
	1																							A A
				K A		1	K		A		2	K		A	1	K		A		2						j l
								2					3				4
			1		1					1				2					2

Степень поляризации суммарного потока излучения определим, используя собственные числа A1 , A2 его матрицы когерентности, определенные соотношениями (2.144). Тогда, с учетом (2.145), запишем:

	A1	A2		A 1		A 1		K				K					A(2)			A 2		(K			K )
			1		2			1						3			1		2			2				4	.	(2.148)
	A1	A2						A	1			A 1					A(2)		A 2
								1						2			1		2
Преобразуем выражение (2.148) к виду взвешенной суммы
		A 1		A 1		K K		3							A(2)		A	2		(K	2	K	4	)
		1	2		1									1			2									,		(2.149)
																									2
		A 1	A 1		A(2)		A	2	1					A 1			A 1			A(2)		A	2
		1	2		1		2							1			2		1			2
где величины
						A 1	A 1								A	2	A	2
						1		2		;					1		2
			1			A 1	A 1				2				A	2	A	2
					1			2						1			2

представляют собой степень поляризации суммируемых потоков, а

коэффициенты

A		1	A		1	K K		3		A 2		A		2	K	2	K	4
	1			2		1			;		1		2
A	1		A	1		(2)	A	2		A	1	A	1		(2)		A	2
						A									A
1			2			1	2			1		2			1		2
										159

учитывают как относительную мощность суммируемых волн, так и взаимную ориентацию систем собственных векторов матриц когерентности этих волн.

В случае если собственные векторы матриц когерентности слагаемых волн попарно совпадают с собственными векторами матрицы когерентности

суммарной волны,			то K1 K2			1,		K3	K4	0	и выражение (2.149)
превращается во взвешенную сумму вида
		A 1	A 1					A(2)	A	2
		1	2					1	2			2 ,	(2.150)
	A 1	A 1	A(2)	A 2	1		A 1	A 1	A(2)		A 2
1		2	1	2		1		2	1		2

весовые коэффициенты которой определяются только величиной относительной мощности слагаемых волн.

2.9. Параметрическое описание суммы коррелированных потоков

излучения с использованием системы матриц Дирака.

Рассмотрим теперь обобщение параметрического описания плоских частично-поляризованных волн на случай коррелированных потоков излучения. До настоящего момента рассматривались только некоррелированные аддитивные потоки излучения, для которых была справедлива теорема Стокса.

Наличие корреляционной связи между потоками излучения (волнами)

приводит к необходимости использования для описания суммарного потока

(4х4) матрицы когерентности

									E	1	t
									1
			|| E 1 *	t E 1 *	t E 2 *	t E 2 *			E	1	t
|| M	jl	||					t ||		2
			1	2	1	2			E	2	t
									1
									E	2	t
									2

160