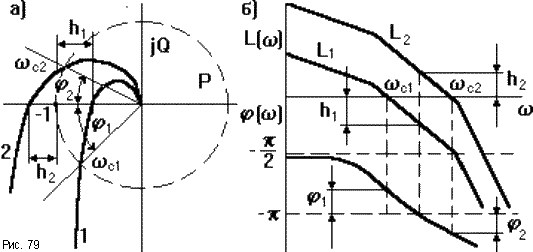
10.3. Анализ устойчивости по лчх

 

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K₁ < K₂. Пусть первая САУ устойчива в замкнутом состоянии, вторая нет.(рис.79).

 

 

Если W₁(p)- передаточная функция первой САУ, то передаточная функция второй САУW₂(p) = KW₁(p), гдеK = K₂/K₁. Вторую САУ можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (безынерционное звено) иW₁(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.

Поэтому ЛАЧХ второй САУ: L₂() = 20lgK + L₁(),

а ЛФЧХ: ₂() =₁().

Пересечениям АФЧХ вещественной оси соответствует значение фазы = -. Это соответствует точке пересечения ЛФЧХ = -линии координатной сетки. При этом, как видно на АФЧХ, амплитудыA₁() < 1, A₂() > 1, что соответствует на САЧХ значениямL₁() = 20lgA₁() < 0 и L₂() > 0.

Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ = -будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулюh₁иh₂, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где = -, но в логарифмическом масштабе.

Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты _c1и _c2, при которых это происходит называютчастотами среза.

В точках пересечения A() = 1 = > L() = 0- ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ _c1 > -(рис.79а кривая 1), то замкнутая САУ устойчива. На рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии = -. И наоборот для неустойчивой замкнутой САУ (рис.79а кривая 2) _c2 <-, поэтому при =_c2ЛФЧХ проходит ниже линии = -. Угол ₁ = _c1-(-)является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии = -до ЛФЧХ.

Исходя из сказанного, критерий устойчивости Наквиста по логарифмическимЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси[-;-1], можно сформулировать так: для того, чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию = -, была больше частоты среза.

 

 

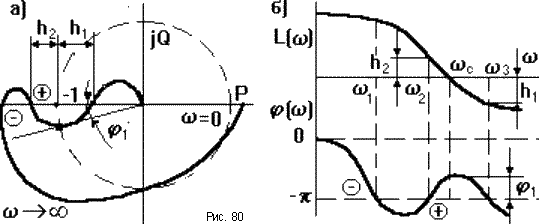
Если АФЧХ разомкнутой САУ имеет сложный вид (рис.80), то ЛФЧХ может несколько раз пересекать линию = -. В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.

Лекция 11.Качество сау

11.1. Теоретическое обоснование метода d-разбиений

 

Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.

Приведем характеристическое уравнение замкнутой САУ к виду:

D(p) = pⁿ + c¹ p^{n -1} + c² p^n-2 + ... + cⁿ = 0,

где c⁰ = a⁰ /a⁰ = 1, c¹ = a¹ /a⁰ и т.д. При некоторых конкретных значенияхc¹ ,c² ,...,cⁿ уравнение имеет единственное решение, то есть единственный набор корней (p¹ , p² ,...,p_n). По их расположению на комплексной плоскости можно судить об устойчивости САУ при заданных параметрах. Если изменить какой-либо параметр САУ, например коэффициента передачи, то изменятся и коэффициенты характеристического уравненияD(p) = 0и станут равнымиc^н1 ,c^н2 ,...,c^нn .Уравнение примет вид:

 

D_н(p) = pⁿ + c^н1 p^{n -1} + c^н2 p^{n -2} + ... + c^нn = 0.

 

Э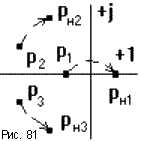то уже другое уравнение и оно также имеет единственное решение(p^н1 ,p^н2 ,...,p^нn ), отличающееся от(p¹ ,p² ,...,pⁿ ). Если плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут плавно изменяться, а его корни будут перемещаться по комплексной плоскости (рис.81).

Каждый уникальный набору коэффициентов c¹ ,c² ,...,cⁿ можно изобразить точкой в пространстве коэффициентов, по осям которого откладываются значения коэффициентовc¹ ,c² ,...,cⁿ . Так уравнению третьей степени соответствует трехмерное пространство коэффициентов (рис.82).

Пусть точка Nс координатами(c_N1 ,c_N2,c_N3)соответствует уравнению, имеющему решение(p_N1,p_N2,p_N3), точка M с координатами(c_M1 ,c_M2 ,c_M3)соответствует уравнению, имеющему решение(p_M1 ,p_M2 ,p_M3). При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению будет перемещаться по некоторой траектории, например из положенияNв положениеM. Этому перемещению будет соответствовать и перемещение корней(p_N1,p_N2,p_N3)на комплексной плоскости в положение(p_M1 ,p_M2 ,p_M3)(аналогично рис.81).

При этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k-й корень примет значениеp_K = j_K, а коэффициенты уравнения будут иметь определенные значенияc_K1,c_K2,c_K3, определяющие в пространстве коэффициентов точкуK. Подставим кореньp_Kв характеристическое уравнение, получим тождество:

 

D(p_K ) = (j_K)³ + cK1(j_K)² + c_K2 (jK ) + c_K3 = 0

Меняя w от -до +, и находя при каждой частоте все возможные сочетания коэффициентовc¹ ,c² ,...,cⁿ, удовлетворяющих уравнению

 

D(j) = (j)ⁿ + c¹ (j)^n-1 + c² (j)^n-2 + ... + cⁿ = 0,

 

можно построить в n-мерном пространстве коэффициентов сложную поверхностьS, разделяющую его на области, называемоеD-областями. Полученное уравнение называетсяуравнением границы D-разбиения.

Переход из одной D-области в другую через поверхностьSсоответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть каждая точка внутри определеннойD-области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначаютD(m)по числу m правых корней.

Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S, можно выявить обозначения всех других областей. Особый интерес представляет областьD(0), которой соответствуют уравнения с полным отсутствием правых корней, называемаяобластью устойчивости. Описанный метод определения областей устойчивости называетсяметодом D-разбиений.

Не обязательно строить сложную n-мерную картинуD-разбиения, можно изменять значения, например, только двух коэффициентов, оставляя другие коэффициенты постоянными. ГраницуD-разбиенияSможно строить не только также и в пространстве конкретных параметров системы, от которых зависят данные коэффициенты.

 

11.2. D-разбиение по одному параметру

 

Пусть необходимо выявить влияние на устойчивоять САУ, например, коэффициента усиления K. Приведем характеристическое уравнение к видуD(p) = S(p) + KN(p), выделив члены, не зависящие от Kв полиномS(p), а в остальных членах, линейно зависящих отK, вынесем его за скобки. ГраницаD-разбиения задается уравнением

 

D(j) = S(j) + KN(j) = 0,  => K = -S(j)/N(j) = X() + jY().

 

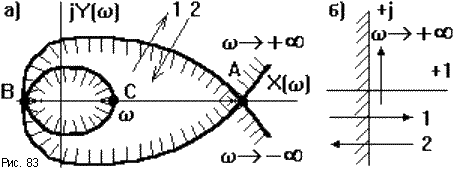
Изменяя w от -до +, будем вычислятьX()иY()и по ним строить точки границыD-разбиения. Пространство коэффициентов представляется системой координатX-Y(рис.83а). Обычно строят только половину кривой (= [0, +), другую половину достраивают симметрично относительно вещественной оси.

Если в плоскости корней двигаться вдоль мнимой оси от -до +и штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль линииD-разбиения при изменении w от -до +и штриховке ее также слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1соответствует аналогичный переход через границуD-разбиения вдоль стрелки1, и наоборот. Если пересекается область с двойной штриховкой (точкиA, В, C), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.

Если известно количество правых корней, соответствующее хотя бы одной D-области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значенииKпроверить систему на устойчивость любым методом.

Есть одна особенность. Так как K- вещественное число, тоY() = 0,поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то естьK = X().