Дробно-рациональные функции

Определение 1. Дробно-рациональной функцией называется выражение вида , где многочлены.

В некоторых учебных пособиях эти функции называются рациональными функциями или рациональной дробью.

Определение 2. Дробь называется правильной, если старшая степень многочлена, находящегося в числителе, меньше старшей степени многочлена в знаменателе, то есть , в противном случае дробь неправильная.

Определение 3. Дробь называется несократимой, если многочлены в числителе и знаменателе не имеют общих корней.

Интегрирование простейших рациональных дробей

Известны 4 простейшие дроби. Интегралы от них вычисляются следующим образом

I. .       Доказательство: .

II. .

Доказательство: .

III. ,      IV.    .

(при эти два интеграла сводятся к первым двум интегралам).

Простейшие дроби III и IY типов преобразуются одинаково по следующей схеме:

1. Выделяется полный квадрат в знаменателе подынтегральной функции

,

где

.

2. Делается замена переменной , и интегралы разбиваются на два, причем интеграл третьего типа сводится к одному табличному типа арктангенса, второму почти табличному типа логарифма знаменателя. Покажем это

.

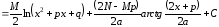Итак, известна процедура приведения интеграла III типа к двум легко вычисляемым интегралам.

Пример.

Вычислить . Поскольку , данный интеграл является интегралом третьего типа. Решаем его, используя вышеприведенную процедуру

.

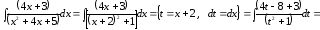
С интегралом IV типа сложнее. После той же замены переменной получаем

.

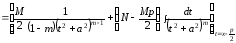Один из интегралов сведен к табличному и вычислен. Для вычисления второго требуется, так называемая, рекуррентная формула, вывод которой осуществляется с помощью интегрирования по частям

,

откуда следует

.

Определяем

,

где

.

Покажем на примерах, как применяется рекуррентная формула.

Пример 1. Вычислить .

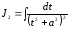Поскольку , применяем рекуррентную формулу

при :

.

Итак, .

Пример 2. Вычислить . Применяем рекуррентную формулу при : , но определено выше, тогда

.

Тогда

.

Пример 3. Вычислить . Преобразуем интеграл, используя вышеуказанную процедуру

.

Поскольку

,

что следует из примера 1, получаем

.

Правила интегрирования дробно-рациональных функций

При вычислении следует руководствоваться правилами.

1. Установить, является ли подынтегральная функция правильной или неправильной дробью. Если дробь неправильная, представить ее в виде суммы целой части и правильной дроби, с помощью "деления углом", или каким либо другим методом выделив ее целую часть.

2. Выяснить, является ли правильная дробь простейшей, если да, то приступить к ее интегрированию.

3. Если дробь не является простейшей, представить ее в виде суммы простейших дробей и после этого приступить к интегрированию.

Замечание. Точное интегрирование дробно-рациональных функций возможно, если многочлен в знаменателе представим в виде произведения простейших множителей, другими словами, известны все его корни.

Рассмотрим интеграл

.

Дробь неправильная . Выделяем целую часть, применяя процедуру "деления углом", напоминающую деление чисел

В результате

.

Примечание. Интегрирование целой части, выделенной из неправильной дроби, трудностей не представляет, поскольку приводит к интегралам от степенных функций. Сложнее с интегрированием правильных дробей, если они не являются простейшими, как в вышеприведенном примере.

Разложение правильной дроби на простейшие

Теорема 1. Из правильной несократимой дроби , , где действительное число, можно выделить простейшую дробь , т.е. .

Доказательство.

.

Распорядимся неопределенным пока коэффициентом так, чтобы был корнем многочлена , то есть . Это возможно, если принять . В соответствии с доказанной выше теоремой . После сокращения на , убеждаемся, что теорема доказана.

Теорема 2. Из правильной несократимой дроби , где

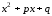корни многочлена , причем , и эти корни не являются корнями многочлена , можно выделить простейшую дробь , то есть следует доказать, что

.

Доказательство.

.

Поскольку и неопределенные пока коэффициенты, потребуем, чтобы . Так как комплексное число, а сумма, произведение и степень комплексного числа - также комплексные числа, левая часть уравнения – есть комплексное число. Но комплексное число равно нулю только в том случае, когда его действительная и мнимая части равны нулю. Таким образом, из одного комплексного уравнения получается система двух алгебраических уравнений относительно и , которые определяются единственным образом и представляют собой действительные числа. Если многочлены с действительными коэффициентами, то . В результате

и

.

Теорема доказана.

Следствие 1 и 2 теорем

.

Таким образом, правильную несократимую дробно-рациональную функцию можно представить в виде суммы простейших дробей только в случае, когда ее знаменатель представим в виде произведения простейших множителей. Таковыми являются либо , когда у знаменателя имеются действительные корни кратности , либо , когда знаменатель имеет комплексно сопряженные корни кратности .

Как следует из формулы, приведенной в следствии, степень каждого множителя в знаменателе показывает количество простейших дробей, порождаемых этим множителем. Другими словами, в приведенной формуле множитель знаменателя приводит к простейшим дробям, выражение порождает простейших дробей.

Правила определения коэффициентов разложения

1. После представления правильной дробно-рациональной функции в виде суммы простейших дробей приводим правую часть формулы к общему знаменателю, следя за тем, чтобы общий знаменатель совпадал со знаменателем разлагаемой дроби.

2. Так как знаменатели дробей в левой и правой частях равенства совпадают, дроби равны, если равны их числители, в результате получаем равенство многочленов, расположенных в левой и правой частях формулы.

3. Поскольку многочлены равны только тогда, когда совпадают коэффициенты при одинаковых степенях переменной, получаем систему уравнений относительно коэффициентов разложения. Доказано (доказательство не приводится), что эта система имеет единственное решение.

4. После определения из полученной системы уравнений значений коэффициентов разложения интегрируем простейшие дроби.

Пример 1.

. Имеем интеграл от дробно-рациональной функции, дробь правильная, несократимая и не являющаяся простейшей. Тогда

.

Отметим, что первый множитель знаменателя дроби дает одну простейшую дробь, так как выражение в скобках в первой степени, второй множитель дает две простейшие дроби, поскольку степень множителя вторая.

После приведения правой части равенства к общему знаменателю, совпадающему со знаменателем дроби в левой части равенства, имеем

.

Эти дроби равны при равенстве их числителей

,

откуда следует

. (*)

Смысл тождественного равенства в том, что многочлены в левой и правой частях равны при любых значениях . Это возможно только при равенстве коэффициентов при одинаковых степенях этих многочленов. В результате приходим к системе уравнений относительно коэффициентов разложения

Решение системы уравнений может быть получено разными способами.

Представляет особый интерес добавление к этой системе дополнительных, "лишних" уравнений, упрощающих получение решения. Рассуждают при этом следующим образом. Тождество (*) предполагает, что равенство справедливо при любых значениях переменной , следовательно, его можно использовать и при конкретных значениях переменной. Значение выбирается так, чтобы не вошло в уравнение наибольшее число неизвестных.

Примем , тогда тождество приводит к уравнению

,

в уравнении осталось только A, определяем его . Из первого уравнения полученной выше системы следует , после чего из второго получаем .

Поскольку к решению системы привлекалось дополнительное уравнение, третье уравнение системы оказалось лишним. Используем его для проверки полученного результата .

Теперь

.

Пример 2. .

Многочлен в знаменателе необходимо представить в виде произведения простейших множителей. Поступаем следующим образом. Перебором вариантов подбирается один из корней знаменателя, в нашем примере это . Делим многочлен на

Тогда , причем второй множитель действительных корней не имеет, поскольку его дискриминант равен . В результате

.

После приведения правой части к общему знаменателю, имеем

,

откуда следует

.

Это тождество приводит к системе уравнений

Добавим к этой системе дополнительное уравнение, полученное из тождества при :

,

откуда следует . Теперь из первого уравнения системы , из последнего уравнения . Проверим результат, подставив полученные значения коэффициентов в оставшееся второе уравнение

.

В итоге

.

Первый интеграл практически табличный, второй является интегралом третьего типа, решаем его, используя описанную выше процедуру.

.

Итак,

.

Пример 3. .

Иногда представление знаменателя дроби в виде произведения простейших скобок может быть осуществлено без определения корней знаменателя. Покажем, как это делается в данном примере

.

Дальнейшее упрощение знаменателя нецелесообразно, так как ни один из полученных квадратных трехчленов не имеет действительных корней. Итак,

.

После приведения дробей к общему знаменателю приходим к тождеству

или

.

Приравниваем коэффициенты при одинаковых степенях многочленов в левой и правой частях тождества

В рассматриваемом случае не удается для упрощения решения системы уравнений привлечь дополнительных уравнений. Однако третье уравнение системы с помощью первого уравнения приводится к виду , откуда имеем . Теперь из последнего уравнения получаем . Из первого уравнения имеем . Подставляя все это во второе уравнение, получаем , откуда следует , после чего . Итак,

.

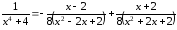Вычисляем интегралы

.

В итоге

.

Примеры для самостоятельного решения

Вычислить интегралы

11.1. , 11.2. , 11.3. ,

11.4. , 11.5. .