ВОЕНЫ АЛЛАХА1АЗАЗАЗАЗ / 0_Введение_сент_9_2008

О.А. Кашина, А.И. Кораблев

случае	D x : x E	n	,	F(x) 0, x 0 .
Целевая функция				f и все функции	fi , вообще

говоря, нелинейны, поэтому такую задачу отыскания условного минимума называют задачей нелиней-

ного программирования.

Задача нелинейного программирования значительно сложнее классической задачи на условный экстремум. Причиной тому – особенность «конструкции» множества D . Граница его, даже если все

функции

fi

дифференцируемы, представляет собой,

вообще говоря, «негладкое» многообразие. Поэтому приведенные выше теоремы мало чем могут помочь в исследовании и решении задачи нелинейного программирования. Отсутствие в классическом анализе необходимого аппарата исследования потребовало разработки современной теории экстремальных задач. С основами этой теории мы познакомимся в рамках данного пособия.

	В классической задаче в любой допустимой
точке	x	равенства	fi x 0 выполнены для всех
i 1, ..., m ,		а в задаче нелинейного программирова-

ния часть ограничений может выполняться в виде

равенств, а	часть – в	виде		строгих неравенств.
Введем	следующие		определения.
Определение 3.		Ограничение с номером i
( i 1, ..., m )	называется		активным (или жест-
ким) в точке x D ,		если		fi x 0 .

14

Методы оптимизации: Часть I

Определение 4.		Ограничение		с
( i 1, ..., m )	называется		пассивным
жестким) в	точке	x D ,	если	fi x

номером i (или не-

0 .

Множество номеров всех активных в точке x
ограничений обозначим		I x .		Таким		образом,
I x i : i 1, ..., m;			fi	x		0 .
Определение	5. Пусть в		задаче			нелинейного
программирования	D x : x E			n	, F x 0, x 0 ;

векторы

x

что вектор

D ,x,

y y

E	m	,	y 0	. Будем говорить,

удовлетворяет условию до-

полняющей нежесткости,

венство

y, F x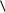

если	выполнено ра-
0.	(3)

			m
	Условие (3) можно записать как yi fi x 0 .
			i 1
Отсюда,		в	силу знакопостоянства	слагаемых,
yi	fi x	0,	i 1, ..., m . Поэтому, если	i -тое огра-

ничение задачи нелинейного программирования пас-

сивно	в	точке	x , то	yi 0 . Таким образом, огра-
ничение		на знак множителя Лагранжа yi			является в
точке	y	активным.		Если же yi 0 (ограничение
на знак		yi в	точке	y пассивно), то	fi x 0 ,

что означает активность i -того ограничения задачи в точке x .

15

О.А. Кашина, А.И. Кораблев

Теорема 4.	Пусть
программирования	D

x

в

:

задаче

n	, F
x E

x

нелинейного

0, x 0 .

Пусть неотрицательные векторы x E							n	,	y	E	m
таковы,		что L x, y L x, y для всех					y 0			. То-
гда	x,	y	удовлетворяет		условию	дополняющей
нежесткости.
	Доказательство. По				условию	теоремы
	f x		y, F x	f x y, F x		, y 0				,
то	есть
			y, F x	y, F x , y 0 .						(4)

Покажем, что отсюда следует

F x 0.

неравенство

(5)

Действительно,

такое, что	f	i

еслиx

найдется значение

i

0	, то, полагая	y	j

(1 i0

m )

для

всех	j 1, ..., m;	j i
yi fi	x y, F x	при

значениях компоненты

из неравенства (4) имеем любых неотрицательных

yi	, что невозможно при

достаточно больших yi .

Итак, (5) имеет место, поэтому с учетом

неотрицательности вектора			x	получаем, что x D .
Так	как векторы	y 0 и			F x 0 ,
	y, F x			0 .	(6)
С другой	стороны, из	(4)		при	y 0 получаем
16

Методы оптимизации: Часть I

y, F x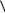

0

.

(7)

Из (6) и (7) следует (3). Что и требовалось.

Теорема 5. программирования

Пусть D

x

взадаче

:x En , F

x

нелинейного

0, x 0 .

Пусть неотрицательные

удовлетворяют условию сти и неравенству

векторы x

дополняющей

n		E	m
E	, y

нежестко-

	, y		L x, y		,
L x

x

0

.

(8)

Тогда вектор	x		– решение

программирования. Доказательство. Из (8)

задачи нелинейного

и (3) получаем

Пусть

имеем

f x

			, F x ,		x 0 .			(9)
f x f x		y
x D .	Тогда	F x 0		и,	так как	y		0 ,
y , F x 0 .		Отсюда и из (9) получаем
f x ,	x D .	Что и		требовалось.

Заметим, что является условным

в условиях теоремы 5 точка минимумом функции L x,

	x
y

по	переменным		x	на неотрицательном		ортанте
En	x : x En ,		xj 0, j 1, ..., n		n -мерного ев-
клидова		пространства.
	Определение 6.			Неотрицательный		вектор
x , y		называется		седловой	точкой	функции
						17

О.А. Кашина, А.И. Кораблев

Лагранжа, если для всех	x 0	и	y 0
ются неравенства

L x , y L x , y L x, y .

выполня-

(10)

Теорема 6. (О связи седловой точки функ-

ции Лагранжа с решением		задачи			нелинейного
программирования)		, y		– седловая точ-
	Если x
ка функции Лагранжа, то вектор					x		– решение
задачи нелинейного	программирования.

Справедливость этого утверждения непосредственно вытекает из теорем 4 и 5.

Теорема 6 – достаточное условие оптимальности, но оно, вообще говоря, не является необходимым. Например, седловых точек не существует в

случае, если

D

. Существуют также задачи не-

линейного программирования, у которых

D

, но

их функция Лагранжа не имеет седловых точек ([2], стр. 238). Тем не менее, для некоторых классов задач нелинейного программирования наличие седловой точки функции Лагранжа является не только достаточным, но и необходимым условием оптимальности (см. теоремы Куна-Таккера в разделе «Выпуклое программирование»).

18