1. Векторы и операции над ними. Компланарность, коллинеарность векторов.

Базис. Координаты вектора в базисе и действия с координатами.

Вектор – это Направленный отрезок.

Векторы, лежащие на одной или на параллельных прямых, называются Коллинеарными.

Векторы, лежащие в одной или в параллельных плоскостях, называются Компланарными. (Рис. 1 и 2).

Рис. 1 Рис. 2

Операции над векторами:

1. Суммой двух векторов A и B называется вектор C = a + b, начало которого совпадает с началом вектора A, а конец – с концом вектора B при условии, что начало вектора B совпадает с концом вектора A (рис. 3–а). Это правило сложения векторов называется еще “Правилом треугольника”.

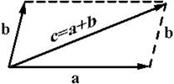
Рис. 3–а Рис. 3–б

Вектор C = a + b можно построить также по “Правилу параллелограмма”: в точке O совместим начала векторов A И B и на этих векторах, как на сторонах, построим параллелограмм. Вектор, совпадающий с диагональю этого параллелограмма с началом в точке O, и является вектором C (рис. 3–а).

С умма векторов обладает как Переместительным свойством (рис. 3–б):

A + B = B + A

Так и Сочетательным (рис. 4):

(a + b) + c = a + (b + c).

Рис. 4

2) Умножение вектора на число-Произведением вектора A на число L называется вектор C = LA, удовлетворяющий следующим условиям:

1.  ;

2.  A коллинеарен вектору A;

3.  , если   > 0 и  , если   < 0.

3)Вычитание векторов- это такой вектор С = А-В

Базис - это такой набор векторов, из которого линейной комбинацией (умножением на число и сложением друг с другом) можно получить любой другой вектор пространства.

Положение координатных осей можно задать с помощью единичных векторов  , направленных соответственно по осям  . Векторы   называются основными или базисными ортами и определяют базис   в трехмерном пространстве.

2. Системы координат: декартова прямоугольная, полярная, цилиндрическая,

сферическая. Связь полярных, цилиндрических и сферических координат декартовыми.

Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс  , вторая – осью ординат  , третья – осью аппликат  ; точка   ‑ начало координат (Рис. 4.4).

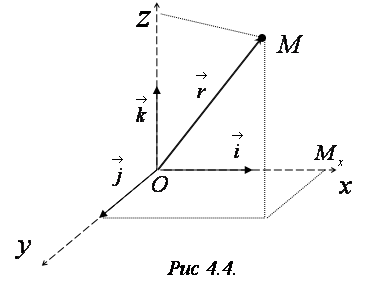
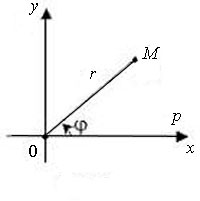
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. 

 

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается  r ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом и обозначается  ф, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Выражение декартовых прямоугольных координат через полярные

x=ρcosφ,y=ρsinφ,(ρ≥0,0≤φ≤2π)

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой z ), которая задаёт высоту точки над плоскостью.

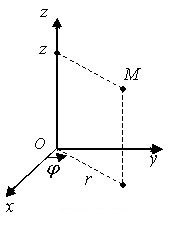Связь между декартовыми прямоугольными и цилиндрическими координатами: x=ρcosφ,y=ρsinφ,z=z, (ρ≥0,0≤φ≤2π).

Сферические координаты.  

Положение точки М в сферической системе координат задается тройкой чисел  r,  φ  и  θ, где  r – расстояние от начала координат до точки  M  ;  φ – угол, образованный проекцией радиус-вектора  на плоскость Оху с положительным направлением оси  Ох ;  θ – угол между положительным направлением оси Ozи радиус-вектором точки М .

Связь между декартовыми прямоугольными и сферическими координатами

x=rcosφcosθ,y=rsinφcosθ,z=rsinθ

 (r≥0,0≤φ≤2π,−π2≤θ≤π2).

3. Простейшие задачи аналитической геометрии в декартовой системе координат: координаты вектора, деление отрезка в данном отношении.

Пусть в пространстве заданы две точки B1(α1,β1,γ1) и B2(α2,β2,γ2), определяющие вектор B1B2¯. Из точки O, которая является началом координат, проведем два направленных отрезка OB1¯ и OB2¯.

Данный рисунок представляет собой геометрическую интерпретацию нахождения разности двух векторов, которой мы и воспользуемся для выведения формулы. Также для удобства введем базисные векторы i, j, k и, разложив по ним вектора OB1¯ и OB2¯, получим:

B1B2¯=OB2¯−OB1¯=α2i+β2j+γ2k−(α1i+β1j+γ1k)==α2i+β2j+γ2k−α1i−β1j−γ1k==(α2i−α1i)+(β2j−β1j)+(γ2k−γ1k)==(α2−α1)i+(β2−β1)j+(γ2−γ1)k.

Отсюда видно, что для того, чтобы найти координаты вектора, необходимо из каждой координаты конца вычесть соответствующую координату начала:

B1B2¯=(α2−α1,β2−β1,γ2−γ1).

Для случая на плоскости формула примет следующий вид:B1B2¯=(α2−α1,β2−β1), где положение точек B1(α1,β1) и B2(α2,β2) определяется двумя координатами.

2. 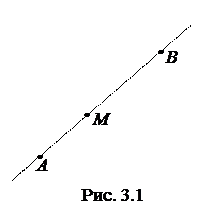  Деление отрезка в данном отношении.

2 Отношением, в котором точка М делит отрезок АВ (рис. 3.1) называется число   .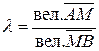

Если точка М находится между точками А и В, то величины направленных отрезков   и   будут одного и того же знака независимо от выбора направления на прямой АВ. В этом случае число l будет больше нуля. Если же точка М находится за пределами отрезка АВ, то число l меньше нуля.

Координаты точки М, делящей отрезок АВ в отношении   можно найти по формулам:

 

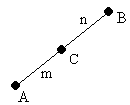
4.  Координаты центра масс системы материальных точек.

координаты центра масс системы есть некоторая сумма произведений масс на радиус-вектора каждой точки, деленное на полную массу системы

 r¯¯C=(r¯¯1m1+ r¯¯2m2)/(m1+m2)

5. Проекция вектора на ось. Свойства проекции. Направляющие косинусы.

Проекцией  вектора   на ось l называется длина вектора  ,   взятая со знаком «+», если вектор   и ось  l  сонаправлены,  и  со знаком «–»,  если   и l  противоположно направлены.  

Если в качестве оси l взять некоторый другой вектор  , то получим проекцию вектора   на вектор  .

Рассмотрим некоторые основные свойства проекций:

1)     проекция вектора   на ось l равна произведению модуля вектора   на косинус угла  между вектором и осью, то есть  ;

2)     проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой; 

3)     проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

6. Скалярное произведение векторов (определение, свойства, выражение в прямоугольных координатах).

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом. Свойства:

7. Векторное произведение векторов (определение, свойства, выражение в прямоугольных координатах).

Векторное произведение — это вектор, который перпендикулярен плоскости, построенной по двум другим векторам

Векторное произведение двух векторов обозначается квадратными скобками:

 

 

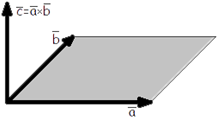
Свойства векторного произведения векторов.

 

1. Геометрический смысл векторного произведения векторов.

 

 Векторным произведением вектора   на вектор   является

вектор  , длина его численно соответствует площади параллелограмма, который построен на векторах   и  .

 Площадь треугольника, строящегося на векторах   и    соответствует одной второй модуля

векторного произведения векторов   и    :

2. Вектор   перпендикулярен векторам   и  , то есть    и  ;

 

3. Вектор   направлен таким образом, что поворот от вектора   к вектору    происходит

против часовой стрелки, если смотришь с конца вектора   (в таком случае тройка векторов  ,   и    – правая).

      4. Длина вектора  равна | | * | | sin<( , ).

 

      5. Векторное произведения двух не нулевых векторов   и    = 0 тогда и только тогда, когда

эти вектора коллинеарны.

       6. Вектор  , равен векторному произведению не нулевых векторов   и    и перпендикулярен

им.

 

      7. 

 

      8. 

 

      9. 

Выражение векторного произведения через координаты.

Используем таблицу векторного произведения векторов i , j и k :

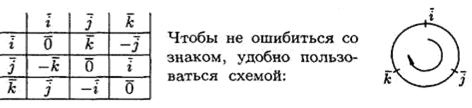
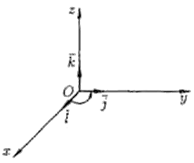
Если направление самого короткого пути от 1 вектора ко 2 совпадает с направлением стрелки, то

произведение векторов равно 3 вектору, а если оно не одинаково — 3 вектор приобретает знак «—».

 

Окончательную формулу легко выразить еще короче:

 

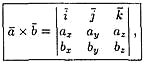
8. Приложения векторного произведения: вычисление площади треугольника (на

плоскости и в пространстве).

Модуль векторного произведения векторов равен удвоенной площади треугольника.

Вычисление площади треугольника:

1.найти векторное произведение.

2.найти длину получившегося вектора

(2)

(1)

9. Смешанное произведение, связь с объемом параллелепипеда, выражение в

координатах. Вычисление объема тетраэдра.

Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.

Рассмотрим произведение векторов , и , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Доказательство. Построим параллелепипед, ребрами которого являются векторы , , и вектор .

Имеем: , , где - площадь параллелограмма, построенного на векторах и , для правой тройки векторов и для левой, где - высота параллелепипеда. Получаем: , т.е. , где - объем параллелепипеда, образованного векторами , и .

Пусть заданы векторы , , . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

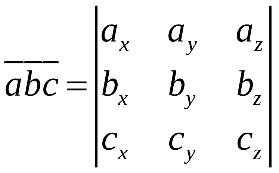
Векторы , и компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( , , )

Объем тетраэдра :

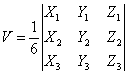
10.Двойное векторное произведение. Формула [[a, b], c] = b(a, c) − a(b, c) .

Двойным векторным или векторно-векторным произведением трех векторов называется выражение вида или Для двойного векторного произведения надо сначала умножить векторно два вектора и , а затем полученное произведение еще раз умножают векторно на третий вектор . Двойное векторное произведение выражается формулами

Правило: Двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор в скобке, умноженный на скалярное произведение двух других. Если векторы заданы своими проекциями

то двойное векторное произведение будет равно:

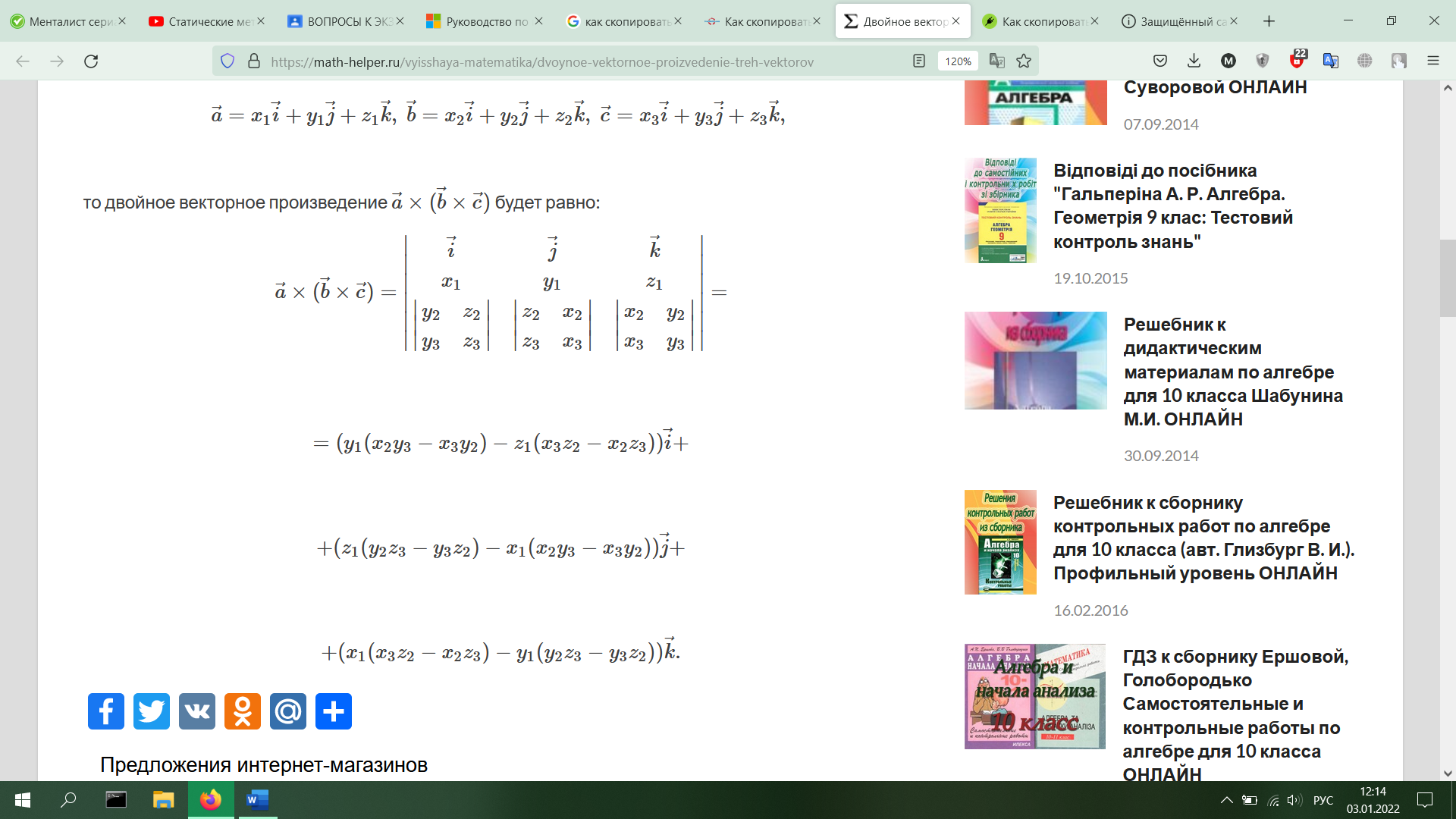
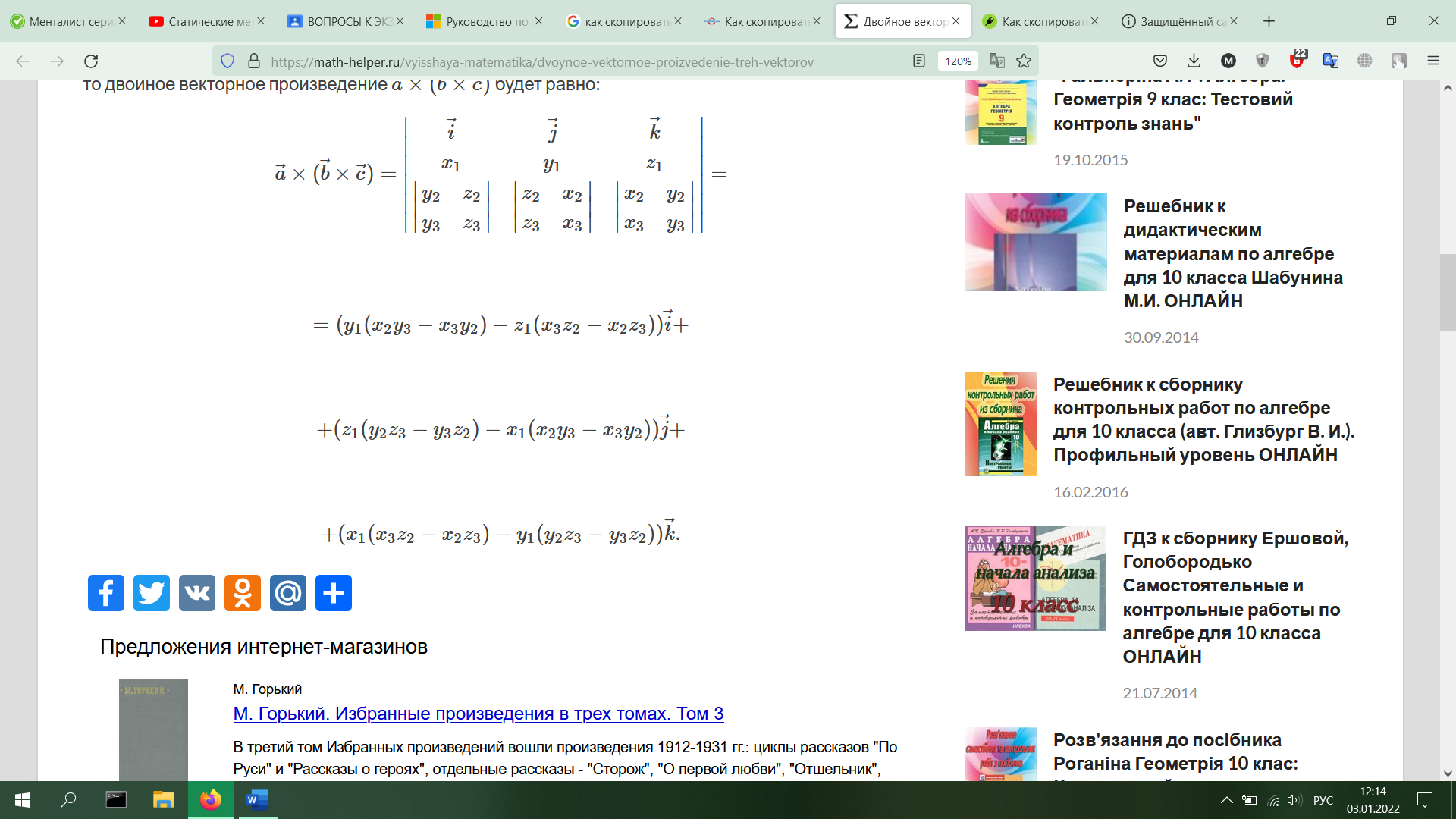
11. Преобразование декартовых прямоугольных координат на плоскости (поворот и параллельный перенос).

В каждом случае координаты точки в старой и новой системах координат связаны формулой (1).

Поэтому достаточно найти вектор переноса начала координат и матрицу перехода от базиса к базису .

а) При параллельном переносе системы координат базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат: . Тогда формула при параллельном переносе:

б) При повороте системы координат на угол начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем Составим матрицу перехода, записывая координаты векторов по столбцам: .

Т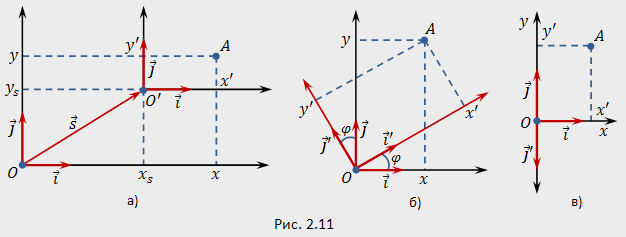 огда формула для поворота системы координат:

Обратные преобразования:

Без a и b.

12.Уравнения линий и поверхностей: явное и параметрическое задание. Алгебраические линии и поверхности. Теорема об инвариантности порядка.

Поверхности:

- параметрические уравнения.

- явное уравнение.

Параметрические уравнении линий:

    

Линия на координатной плоскости называется алгебраической, если в некоторой декартовой прямоугольной системе координат уравнение линии является алгебраическим.

Алгебраической поверхностью называется множество всех точек М(x,y,z) геометрического пространства, координаты которых в декартовой прямоугольной системе координат удовлетворяют алгебраическому уравнению

Степень целой рациональной функции называется порядком алгебраической поверхности.

Поверхности, заданные относительно декартовой системы координат уравнениями

,

Эти уравнения называются общими уравнениями поверхности первого и второго порядка.

Теорема об инвариантности порядка.

Если в некоторой ДСК кривая задается ур-нием порядка n, то в любой другой системе координат эта линия задается ур-нием такого же вида, такого же порядка.

Инвариантно-т.е. независимо от выбора системы координат.

(расстояние)

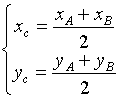середина отрезка (координат)

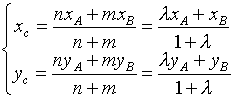формулы деления отрезка в данном отношении.

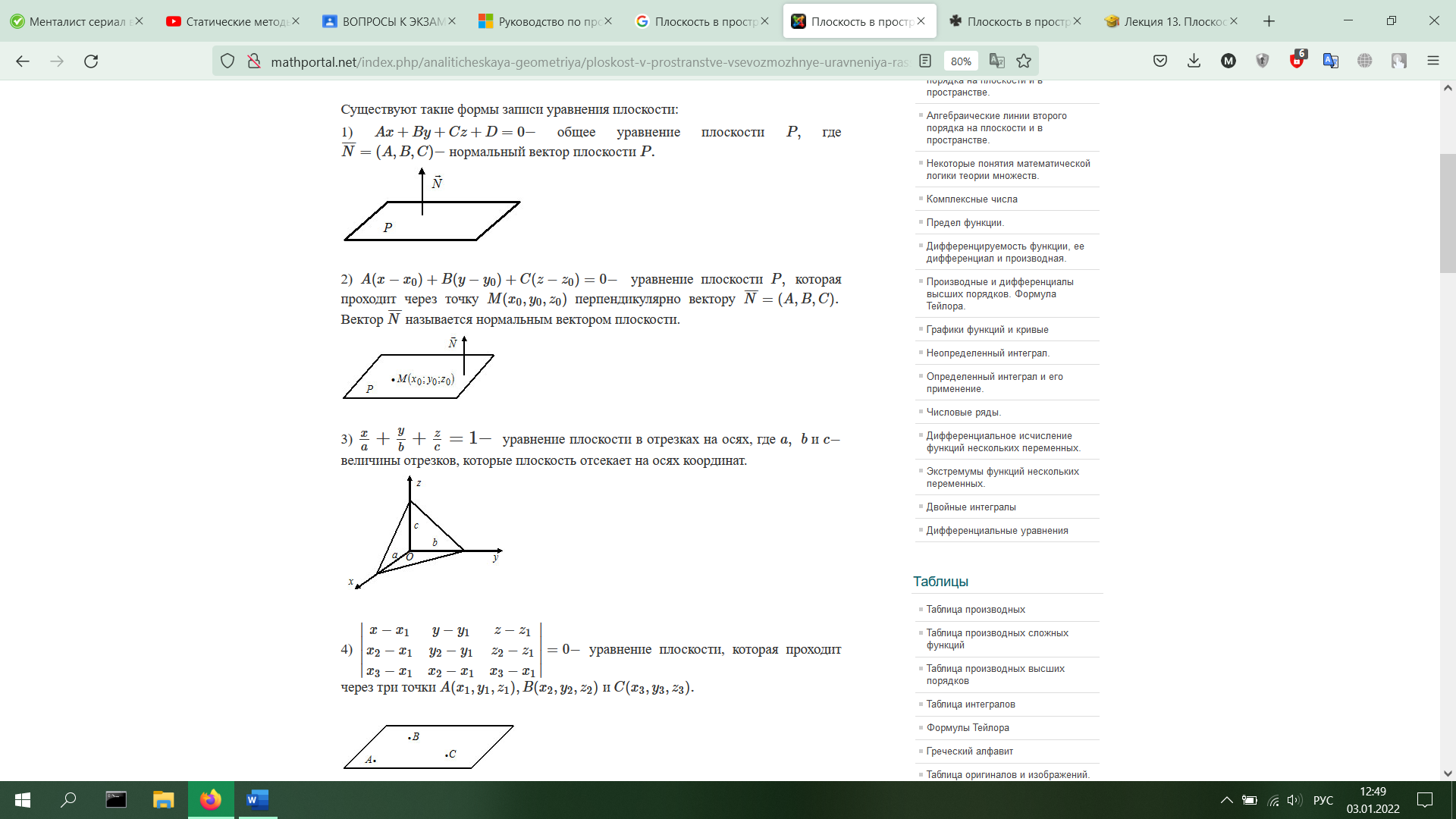
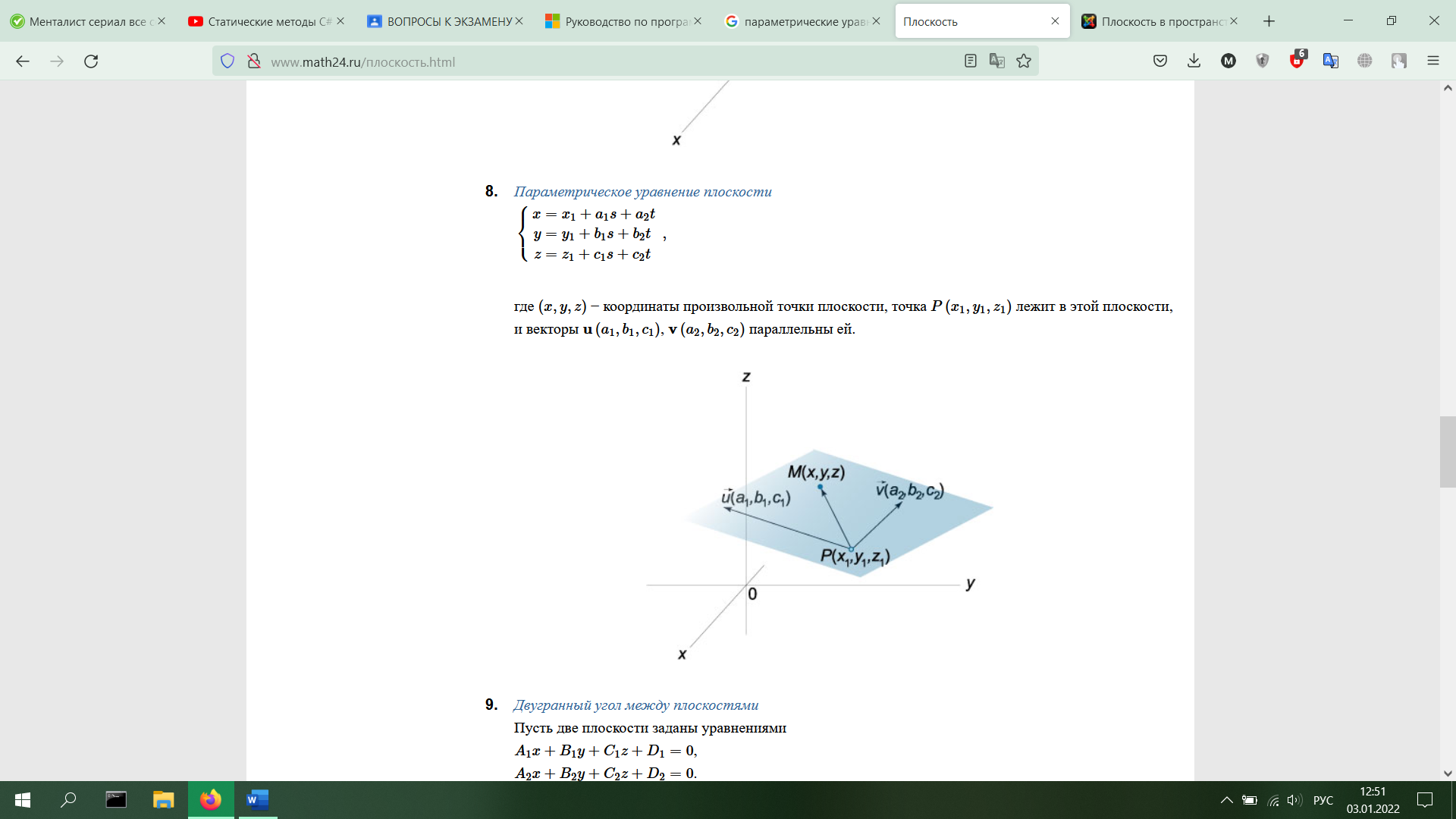
13.Плоскость в пространстве. Различные виды уравнений: общее уравнение, уравнение по вектору нормали и точке, уравнение по трем точкам, уравнение в отрезках, параметрические уравнения плоскости..

14.Уравнения прямой в пространстве (канонические, параметрические, по 2 точкам). Уравнение прямой как пересечение пары плоскостей. Взаимное расположение двух прямых.

Канонические уравнения прямой:

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор  данной прямой, то  канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора  не равны нулю.

Уравнение по двум точкам:

Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами: