
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
Вывод уравнения гиперболы
Введем прямоугольную систему координат. Пусть фокусы гиперболы
лежат
на оси Ох,
причем
 -
середина отрезка
-
середина отрезка
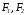 ,
тогда
,
тогда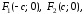 т. е.
т. е.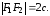 Пусть
Пусть – произвольная точка гиперболы. Величины
– произвольная точка гиперболы. Величины –фокальные
радиусы
точки
М
гиперболы.(чертеж
17.)
–фокальные
радиусы
точки
М
гиперболы.(чертеж
17.)

Чертеж 17.
По определению гиперболы:
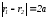 ,
отсюда
,
отсюда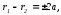 где
где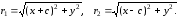
Следовательно,
уравнение
 имеет вид:
имеет вид:
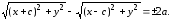 (7)
(7)
Умножим
равенство (7) на
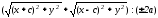 ,
получим:
,
получим:
(8)
Сложим уравнения (7) и (8), получим:
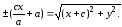 (9)
(9)
Возведем (9) в квадрат:
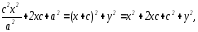 следовательно,
имеем:
следовательно,
имеем:

Пусть
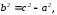 так как
так как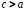
 ,
отсюда имеем уравнение:
,
отсюда имеем уравнение:
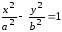 (10)
(10)
где (10) каноническое уравнение гиперболы с центром в начале координат.
Соответственно, уравнение
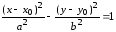

где
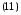 каноническое уравнение гиперболы с
центром в точке
каноническое уравнение гиперболы с
центром в точке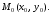
Числа a и b соответственно действительная и мнимая полуоси гиперболы.
Исследование свойств гиперболы по ее уравнению
1) Пересечение гиперболы с осями координат:

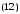
Очевидно, что гипербола состоит из двух ветвей: правой и левой, простирающихся в бесконечность.
В
уравнении (12) положим, что y=0,
получим:
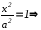
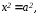 отсюда
отсюда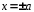 .
Следовательно, точки
.
Следовательно, точки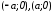 являются точками пересечения гиперболы
с осью
являются точками пересечения гиперболы
с осью (чертеж
18.).
(чертеж
18.).
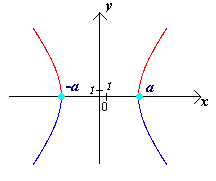
Чертеж 18.
Положим,
что в уравнении (12) х=0, и получим:
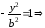
 ,
следовательно, уравнение гиперболы не
пересекает ось
,
следовательно, уравнение гиперболы не
пересекает ось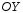 .
.
ЗАМЕЧАНИЕ:
Если мнимая ось гиперболы имеет длину
2a и направлена по оси (OX), а действительная
ось длиной 2b совпадает с осью (OY), то
уравнение гиперболы имеет вид:
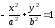 .
[1.С.107-108]
.
[1.С.107-108]
Определение
3.2.
Гиперболы, заданные уравнениями
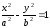 и
и
 ,
называются сопряженными гиперболами.
,
называются сопряженными гиперболами.
Определение 3.3. Если a=b, гипербола называется равносторонней.
2) Симметрии гиперболы относительно координатных осей и:
Пусть
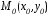 принадлежит гиперболе, то есть
принадлежит гиперболе, то есть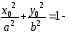 верное
равенство. Точка
верное
равенство. Точка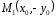 симметрична точке
симметрична точке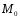 относительно
оси ОХ:
относительно
оси ОХ:
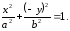
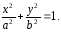 -
верное равенство. Следовательно,
-
верное равенство. Следовательно,
 принадлежит
гиперболе, следовательно, гипербола
симметрична относительно ОХ.
принадлежит
гиперболе, следовательно, гипербола
симметрична относительно ОХ.
Точка
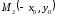 симметрична точке
симметрична точке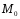 относительно оси ОУ, следовательно,
гипербола симметрична относительно
оси ОУ.
относительно оси ОУ, следовательно,
гипербола симметрична относительно
оси ОУ.
Точка
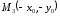 симметрична
точке
симметрична
точке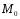 относительно О (центра), отсюда следует,
что гипербола симметрична относительно
начала координат. [1.С.108]
относительно О (центра), отсюда следует,
что гипербола симметрична относительно
начала координат. [1.С.108]
3) Асимптоты гиперболы:
Текущая точка гиперболы при движении по ней в бесконечность неограниченно приближается к некоторой прямой, которая называется асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие уравнения:
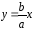 и
и
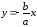 ,
,
Пусть
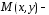 текущая
точка гиперболы,
текущая
точка гиперболы,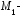 ее
проекция на ось абсцисс. Прямая
ее
проекция на ось абсцисс. Прямая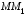 пересекает
прямую
пересекает
прямую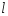 ,
заданную указанным уравнением в точке
,
заданную указанным уравнением в точке .
Докажем: что
.
Докажем: что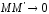 при
при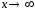 .
.
Доказательство:
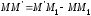 .Расстояние
.Расстояние
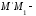 это
ордината точки
это
ордината точки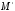 ,
лежащей на прямой
,
лежащей на прямой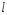 .
Она равна
.
Она равна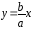 .
Расстояние
.
Расстояние это ордината точки
это ордината точки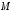 гиперболы, которую находим из её
канонического уравнения:
гиперболы, которую находим из её
канонического уравнения: Тогда
Тогда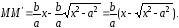

Умножим
и разделим равенство (13) на (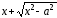 ),следовательно,
получим:
),следовательно,
получим:
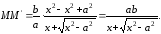
При
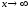 знаменатель дроби неограниченно
увеличивается, следовательно, дробь
стремится к нулю.
знаменатель дроби неограниченно
увеличивается, следовательно, дробь
стремится к нулю.
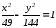 -
уравнение гиперболы, в которой
-
уравнение гиперболы, в которой
 а
а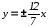 -
являются асимптотами гиперболы. (чертеж
19.)
[1.С.108]
-
являются асимптотами гиперболы. (чертеж
19.)
[1.С.108]

Чертеж 19.
4) Фокусы гиперболы:
Пусть
фокусы гиперболы лежат на оси Ох.
Межфокусное расстояние гиперболы равно
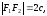 причем
причем
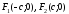 .
Заметим, что
.
Заметим, что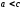 по определению гиперболы.
по определению гиперболы.

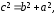
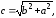
Следовательно,
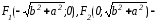 фокусы
гиперболы. [1.С.109]
фокусы
гиперболы. [1.С.109]
5) Директориальное свойство гиперболы:
Определение
3.4.
Директрисами гиперболы
называются
прямые, параллельные канонической оси
ОУ и отстоящие от этой оси на расстояние
 .
.
Уравнения
директрис гиперболы имеют вид:
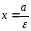 и
и [5.С.122]
[5.С.122]
6) Эксцентриситет гиперболы:
Определение
3.5.
Отношение
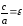 называется эксцентриситетом гиперболы.
Так как
называется эксцентриситетом гиперболы.
Так как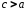 ,
то
,
то
Если
при постоянном значении
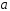 ,
число
,
число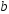 будет изменяться от нуля до бесконечности,
то
будет изменяться от нуля до бесконечности,
то
 будет измениться от
будет измениться от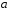 до бесконечности. Если
до бесконечности. Если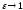 ,
то гипербола будет стремиться к лучам
(чертеж
20.).
,
то гипербола будет стремиться к лучам
(чертеж
20.).
Чертеж 20.
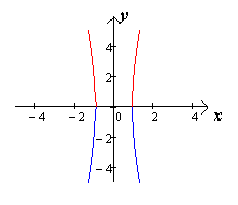
Если
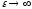 ,
то гипербола будет стремиться к
параллельным прямым (чертеж
21.).
[1.С.109]
,
то гипербола будет стремиться к
параллельным прямым (чертеж
21.).
[1.С.109]
Чертеж 21.
7) Касательная к гиперболе:
Уравнение
касательной к гиперболе
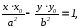 ,
где
,
где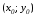 -
координаты точки касания, а
-
координаты точки касания, а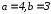 соответственно действительная и мнимая
полуоси гиперболы (чертеж
22.).
соответственно действительная и мнимая
полуоси гиперболы (чертеж
22.).
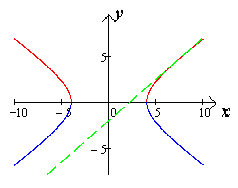
Чертеж 22.
Изображение гиперболы
Построим гиперболу с действительной осью равной 4 и мнимой осью равной 4.
Построение без использования ИКТ: Для построения гиперболы задаем прямоугольную систему координат с центром в точке О и единичный отрезок. Строим прямоугольник со сторонами 2a=4,2b=4, проводим диагонали прямоугольника. Выполняем построение ветвей гиперболы так, чтобы координаты точек (-2;0),(2;0) являлись их вершинами, и ветви гиперболы не пересекали диагоналей прямоугольника.(чертеж 23.)

Чертеж 23.
С использованием ЭСО- Mathcad:
Полученное
уравнение линии имеет вид:
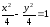 .
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
.
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
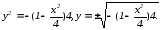 (чертеж
24.)
(чертеж
24.)
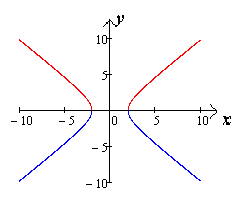
Чертеж 24.
Построим гиперболу с действительной осью равной 10 и мнимой осью равной 8.
а) Построение без использования ИКТ: Для построения гиперболы задаем прямоугольную систему координат с центром в точке О и единичный отрезок. Строим прямоугольник со сторонами 2a=10,2b=8, проводим диагонали прямоугольника. Выполняем построение ветвей гиперболы так, чтобы координаты точек (0;4),(0;-4) являлись их вершинами, и ветви гиперболы не пересекали диагоналей прямоугольника.(чертеж 25.)
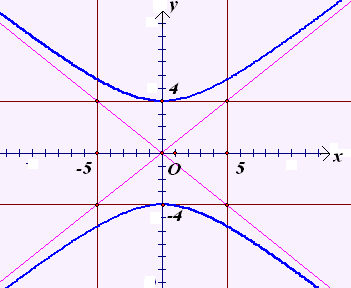
Чертеж 25.
b) С использованием ЭСО- Mathcad:
Полученное
уравнение имеет вид:
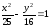 .
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
.
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
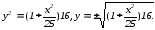 (чертеж
26.)
(чертеж
26.)
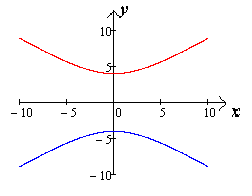
Чертеж 26.
ПАРАБОЛА
Определение 4.1.Парабола- это геометрическое множество точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус). [8.С.589]
