Динамический хаос (ИПИС, ФКС)

В центре каждой ячейки Бенара жидкость движется вверх, а по краям опускается вниз (см. рис. 54). Это явление было объяснено позже Рэлеем в 1916 году и с тех пор называется конвекцией Рэлея-Бенара (Rayleigh-Benard convection). Рэлей показал, что конвекционное течение в виде валов возникает лишь при выполнении условия R Rc , где R – так называемое число Рэлея, а Rc – его критическое значение, равное

Rc			4
		a2	,	(54)
			(1 a2 )3

где a h l – безразмерный параметр, зависящий от геометрии конвективных валов, и равный отношению высоты h вала к его ширине l (см. рис. 55).

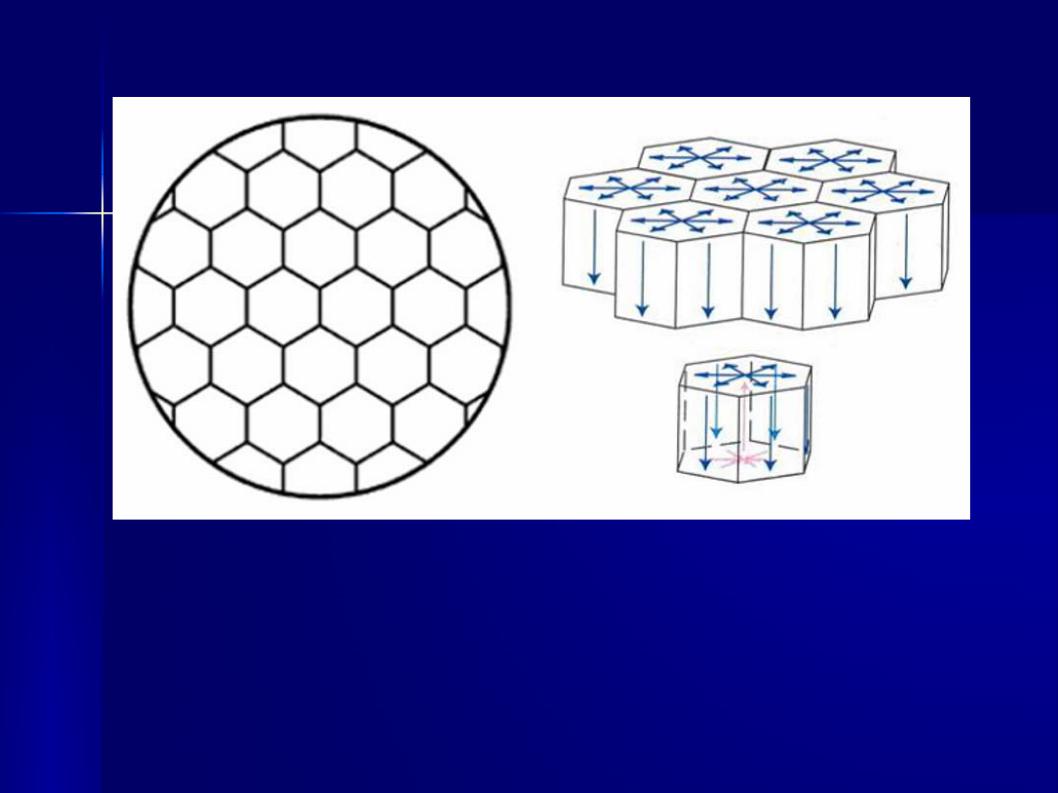
Рис. 54. Схематичное изображение ячеек Бенара. В центральной части каждой ячейки жидкость поднимается вверх, а вблизи вертикальных граней опускается вниз.

На самом деле имеется ещё так называемая конвекция Марангони (Marangoni convection), где пространственные структуры возникают за счёт зависимости от температуры коэффициента поверхностного натяжения жидкости. Такую конвекцию, по-видимому, и наблюдал в своих опытах Бенар.

Модель Лоренца

В 1963 году американский метеоролог Эдвард Лоренц, занимавшийся проблемами прогноза погоды, опубликовал в журнале «Journal of Atmospheric Sciences» статью

«Детерминированное непериодическое течение». Эта работа была посвящена исследованию модельной нелинейной системы трёх обыкновенных дифференциальных уравнений первого порядка, которая получалась как результат определённых приближений при анализе задачи о конвекции в подогреваемом снизу слое жидкости. При численном решении системы на компьютере Лоренц обнаружил установление в системе хаотического режима.

Рассмотрим более подробно, как возникает хаос в модели Лоренца. Для этого обратимся к задаче о конвекции жидкости в подогреваемом снизу слое.

Рассмотрим слой жидкости глубины h , находящийся в поле тяжести. Пусть на верхней границе слоя поддерживается постоянная температура T0 , а на нижней границе

– T0 T (см. рис. 55).

Рис. 55. Конфигурация течения, возникающего при конвекции в подогреваемом снизу слое жидкости.

Из-за того, что нагретая жидкость легче холодной, при достаточно большой разности температур в жидкости возникает конвекционное течение, описание которого и составляет предмет исследования.

В этой задаче мы имеет дело с распределённой системой – состояние жидкости характеризуется меняющимися во времени полями распределения скорости v(x, y, z,t), плотности (x, y, z,t) и температуры T (x, y, z,t). Другими словами, для того, чтобы задать состояние системы в некоторый момент времени необходимо задать величины v , и T для каждой точки жидкости, а т.к. таких точек бесконечное количество, то нашу распределённую систему формально можно считать динамической системой с бесконечно большим числом динамических переменных, и, соответственно, её фазовое пространство также является бесконечномерным.

Выпишем уравнения, которые описывают изменение во времени полей v , и T :

1) Первое уравнение – уравнение Навье-Стокса. Это основное уравнение гидродинамики, которое является аналогом II закона Ньютона

	v		p 2 v f ,
		(v )v
	t

где p – давление, – коэффициент вязкого трения (динамическая вязкость), – оператор набла, f – поле массовых сил. В нашем случае f g , поэтому получим

v (v )v p 2 v g . (55)t

2) Уравнение непрерывности

t ( v) 0 ,	(56)
3) Уравнение теплопроводности
T
t (T v) 2T ,	(57)
где – коэффициент температуропроводности.

4) Уравнение, описывающее закон теплового расширения жидкости

0 (1 (T T0 )) ,

(58)

где – коэффициент теплового расширения.

В результате получаем следующую систему уравнений:

vt

(v )v p 2 v g

	( v) 0
t		(59)

T (Tv) 2Tt

0 (1 (T T0 ))

Точно решить систему (59) не представляется возможным, поэтому мы рассмотрим её приближённое решение.

Для этого сначала сделаем некоторые упрощения:

1)Ограничимся рассмотрением двумерной задачи, т.е. будем считать систему бесконечно протяжённой вдоль оси z , перпендикулярной плоскости рис. 55. Будем считать, что

все переменные величины не зависят от z и что z-компонента скорости отсутствует. Другими словами, будем рассматривать только плоское течение жидкости.

2)Воспользуемся приближением Буссинеска. Оно состоит в том, что жидкость предполагается слабо сжимаемой и зависимость плотности от температуры учитывается только в одном месте – в правой части уравнения НавьеСтокса.