
- •Методы многомерной оптимизации.
- •Для удобства графической иллюстрации методов определим представление функции в виде линий уровня
- •Проведем сечения поверхности равно отстоящими плоскостями, которые параллельны плоскости изменения переменных x1 и
- •функция Химмельблау
- •Все методы многомерной оптимизации делятся на два класса
- •Основные свойства градиента:
- •Алгоритм
- •начало
- •Симплексный метод
- •5. Сравниваем значения функции
- •начало
Симплексный метод
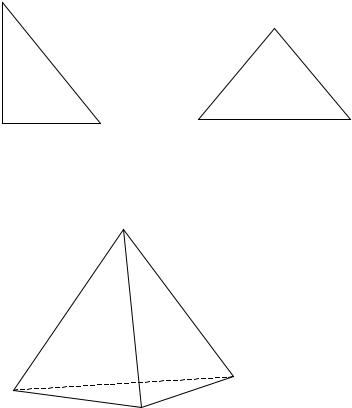
Симплексом в n-мерном пространстве называется выпуклый многоугольник с n+1 вершино
n=2 треугольник
n=3 тетраэдр
11

|
|
|
Алгоритм |
|
|
|
|
|
(0) |
||
|
|
|
|
|
|
|
|
|
|
||
1. Дана функция 2x переменных f ( x ), точность ε, параметр h, начальное приближение x |
|||||||||||
2. Вычисляем координаты вершин симплекса |
|
|
|
|
|
|
|
||||
(1) |
(0) |
(2) |
(0) |
|
h |
(3) |
(0) |
|
0 |
|
|
x |
x |
x |
x |
|
|
x |
x |
|
|
||
|
|
|
|
|
0 |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
(1) |
|
(2) |
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. Вычисляем значения функции |
F1 f ( x |
) |
F2 f ( x |
) F3 |
f ( x |
) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
худ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Определяем худшую вершину |
|
x |
, Fхуд |
и координаты отраженной вершины, |
|||||||||||||||||||||||||||||||||||||||
она будет лежать на прямой исходящей из худшей вершины и проходящей через |
|
|
|||||||||||||||||||||||||||||||||||||||||
середину противоположной грани |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отр |
||||||
ср |
|
ост1 ост2 |
|
ср |
худ |
ост1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
x |
0.5*( x |
x |
|
); |
V x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
отр |
худ |
|
|
отр |
ост1 |
ост2 |
худ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
x |
2 |
V; |
x |
x |
|
x |
|
x |
|
худ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ост2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
отр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Fотр |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f ( x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12
5. Сравниваем значения функции |
Fотр Fхуд |
6. Условие выполняется. За новый симплекс принимаем симплекс с вершиной
отр |
худ |
|
x |
вместо x |
и повторяем с пункта 3 |
7.Условие не выполняется. Проверяем условие окончания h< ε
8.Условие окончания выполняется. Выводим координаты и значение функции лучшей вершины
(0) |
|
9. Условие не выполняется. За x |
принимаем лучшую вершину последнего |
симплекса, уменьшаем длину грани h=h/3 и повторяем с пункта 2.
13
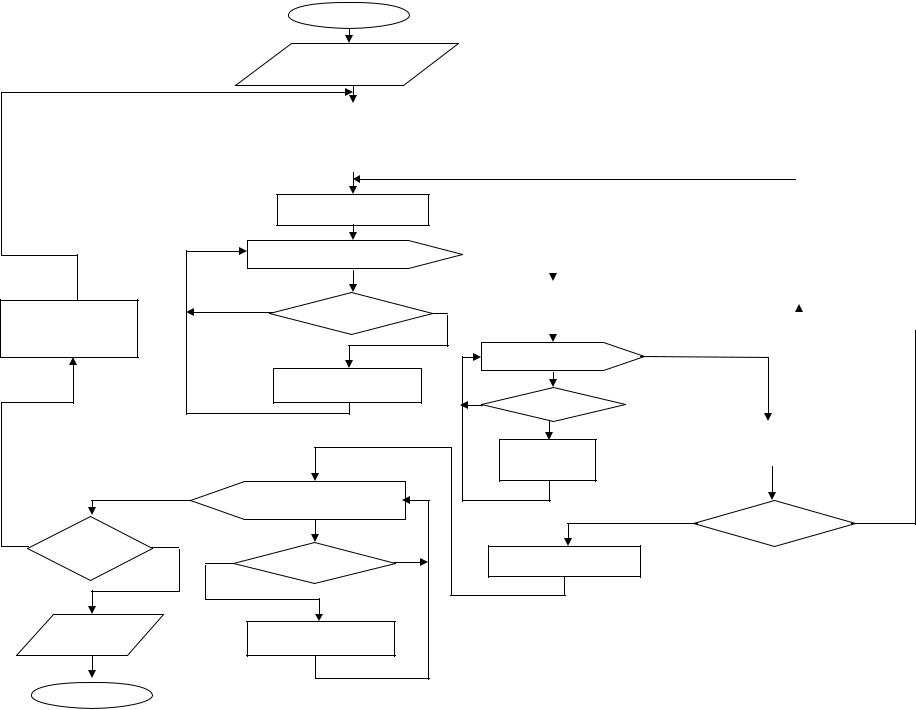
начало
(0)
x ,h, || f ( x )
(1) |
|
(0) |
(2) |
(0) |
h |
(3) |
(0) |
0 |
|
(1) |
(2) |
(3) |
|
x |
x |
: |
x |
x |
|
|
: x |
x |
|
: |
F1 f ( x ) : |
F2 f ( x |
) : F3 f ( x ) |
|
|
|
|
|
|
0 |
|
|
h |
|
|
|
|
|
|
Fxud:=F1: kx:=1 |
|
|
i:=1шаг 2 до 3 |
(0) |
(kl) |
Fi>Fxud |
x |
x |
|
|
|
Fxud:=Fi: kx:=i |
|
|
i:=1 шаг 1 до 3 |
|| h ||<0 |
Fi<Fl |
|
|
|
|
|
(kl) |
Fl:=Fi: kl:=i |
x |
,Fl |
|
конец
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(kx) |
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
x |
: Xot : |
Fk : Fot |
|
||
|
s : 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i:=1шаг 1 до 3 |
||
|
i≠kx |
|
|
|
(i) |
s : s |
x |
|
|
|
(kx) |
|
Xot s |
x |
: Fot f (Xot) |
|
Fot<Fxud
Fl:=F1: kl:=1 |
Пример: |
|
f (x , x |
2 |
) 8x |
2 |
4x x |
2 |
5x |
2 |
|||
1 |
|
|
1 |
1 |
|
2 |
||||
|
|
|
1 |
|
|
|
|
|
||
h=1, eps=0.2 |
x |
0 |
|
|
|
14 |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
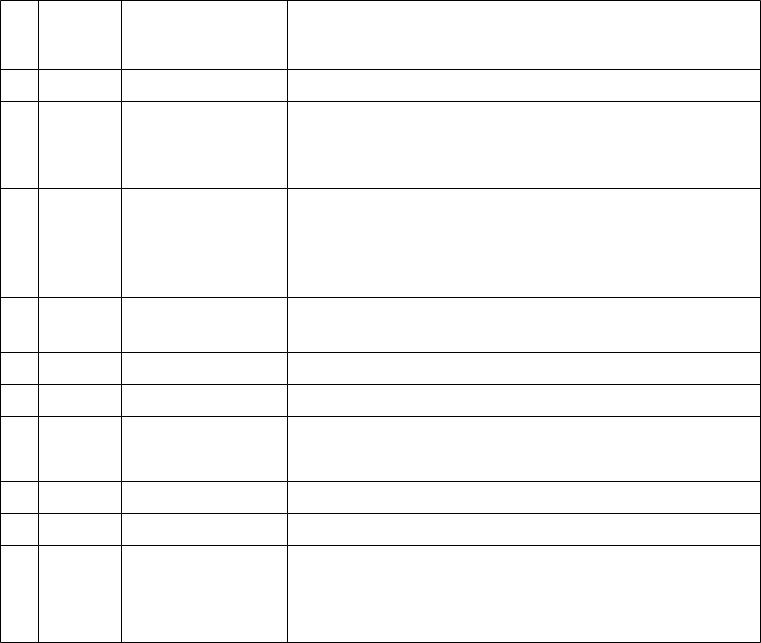
№ |
x1 |
x2 |
f(x1,x2) |
h |
точки симплекса и примечания |
|
||||
1 |
1.00 |
1.00 |
17.0 |
|
1 |
симплекс т.1,2,3 |
т.2 |
худшая отражаем |
|
|
2 |
2.00 |
1.00 |
45.0 |
|
|
|
|
|
|
|
3 |
1.00 |
2.00 |
36.0 |
|
|
|
|
|
|
|
4 |
0.00 |
2.00 |
20.0 |
|
|
удачно симплекс 1,3,4 |
т.3 худшая |
|
||
|
|
|
|
|
|
|
отражаем |
|
|
|
5 |
0.00 |
1.00 |
5.00 |
|
|
удачно симплекс 1,4,5 |
т.4 худшая |
|
||
|
|
|
|
|
|
|
отражаем |
|
|
|
6 |
1.00 |
0.00 |
8.00 |
|
|
удачно симплекс 1,5,6 |
т.1 худшая |
|
||
|
|
|
|
|
|
|
отражаем |
|
|
|
7 |
0.00 |
0.00 |
0.00 |
|
|
удачно симплекс 5,6,7 |
т.6 худшая |
|
||
|
|
|
|
|
|
|
отражаем |
|
|
|
8 |
-1.00 |
1.00 |
9.00 |
|
|
неудачно 1>0.2 h=h/3 = 0.33 |
|
|||
1 |
0.00 |
0.00 |
0.00 |
|
0.33 |
симплекс т.1,2,3, т.2 худшая отражаем |
|
|||
2 |
0.333 |
0.00 |
0.889 |
|
|
|
|
|
||
3 |
0.00 |
0.333 |
0.556 |
|
|
|
|
|
||
4 |
-0.333 |
0.333 |
1.00 |
|
|
неудачно 0.33>0.2 |
h=h/3 = 0.11 |
|
||
1 |
0.00 |
0.00 |
0.00 |
|
0.11 |
симплекс т.1,2,3 т. 2 худшая отражаем |
|
|||
2 |
0.111 |
0.00 |
0.0988 |
|
|
|
|
|
||
3 |
0.00 |
0.111 |
|
|
0.00 |
|
|
|
|
|
0.0617 |
|
f ( x ) 0.000 |
|
|
|
|||||
|
Ответ: |
x |
|
|
|
|
|
15 |
||
4 |
-0.111 |
0.111 |
0.111 0.00 |
неудача 0.11<0.2 |
ответ т. 1 |
|||||
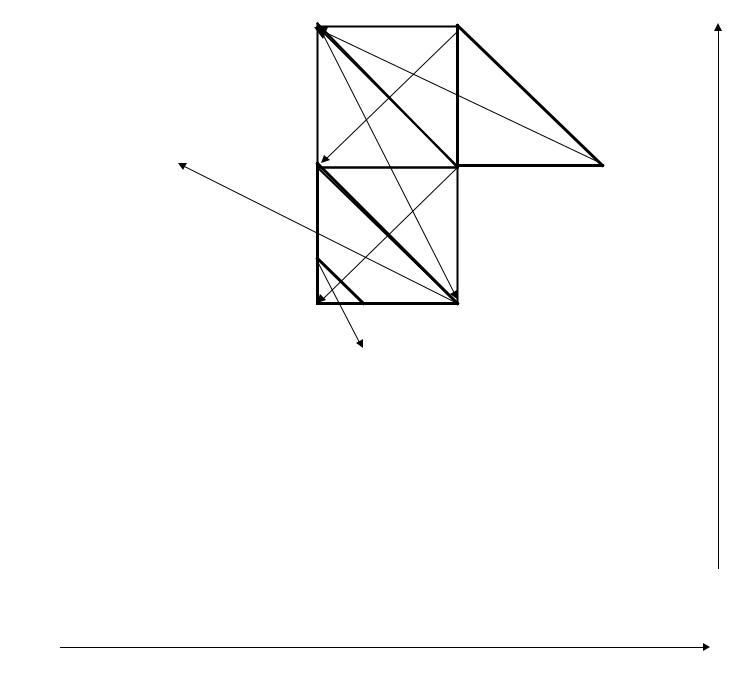
20 |
36 |
x2
9
5
17 45
0.89
0 |
0.56 |
8 |
|
||
|
1.00 |
|
x1
16
