Schisla_1

ностями

Ln(x) = f(x0) + f(x0, x1)(x − x0) + f(x0, x1, x2)(x − x0)(x − x1) + ...+ +f(x0, x1, x2, . . . , xn−1)(x − x0)(x − x1) . . . (x − xn−2).

Ести сделать замену x = x0 + th, то x − xi = (t − i)h, а выражения для

разделенных разностей примут вид

∆y0

∆2y0

∆n−1y0

f(x0, x1) =

, f(x0, x1, x2) =

, . . . , f(x0, x1, . . . , xn−1) =

.

h

2!h

2

n

1

(n − 1)!h −

Теперь интерполяционный многочлен Ньютона для точки x, располо-

женной в начале таблицы, можно записать в виде

Ln(x0 +th) = y0 +

t

∆y0 +

t(t − 1)

∆2y0

+. . .+

t(t − 1) . . . (t − n + 2)

∆n−1y0,

(n − 1)!

1!

2!

где t = (x − x0)/h.

2. Интерполяционная формула Ньютона для конца таблицы (интерполяция назад)

Для конца таблицы интерполяционная формула Ньютона с разделенными разностями записывается для узлов xn−1, xn−2, . . . , x0

Ln(x) = f(xn−1) + f(xn−1, xn−2)(x − xn−1)+ +f(xn−1, xn−2, xn−3)(x − xn−1)(x − xn−2) + . . . +

+f(xn−1, xn−2, xn−3, . . . , x0)(x − xn−1)(x − xn−2) . . . (x − x1).

После замены x = xn−1 + th (x − xi = (t + n − 1 − i)h) для разделенных разностей получаются выражения

f(xn−1, xn−2) = f(xn−2, xn−1) = ∆yn−2 ,

1!h

∆2yn−3

f(xn−1, xn−2, xn−3) = f(xn−3, xn−2, xn−1) = 2!h2 ,

∆n−1y0

f(xn−1, xn−2, . . . , x0) = f(x0, x1, . . . , xn−1) = (n − 1)!hn−1 ,

31

Теперь интерполяционный многочлен Ньютона для конца таблицы прини-

мает вид

L

(x

+th) = y

+

t

∆y

+

t(t + 1)

∆2y

+...+

t(t + 1)...(t + n − 2)

∆n−1y

,

n−1

n−1

n−2

n−3

(n − 1)!

n

1!

2!

0

где t = (x − xn−1)/h.

3.8Интерполяционные формулы Гаусса

Интерполяционные многочлены Гаусса строятся для значений x, находящихся в середине таблицы.

Первая формула Гаусса.

Первая формула Гаусса получается, если в качестве узлов интерполяции выбраны x0, x1, x−1, x2, x−2, ..., xm, x−m при n = 2m + 1 (если n = 2m, последний узел отбрасывается). Формула Ньютона с разделенными разностями для таких узлов имеет вид

Ln(x) = f(x0) + f(x0, x1)(x − x0) + f(x0, x1, x−1)(x − x0)(x − x1)+ +f(x0, x1, x−1, x2)(x − x0)(x − x1)(x − x−1) + ...+

+f(x0, x1, x−1, ..., xm, x−m)(x − x0)(x − x1)(x − x−1)...(x − xm).

Здесь имеются разделенные разности двух типов

∆2k−1y−(k−1)

f(x0, x1, x−1, ..., xk) = f(x−(k−1), ..., x0, ..., xk) = (2k − 1)!h2k−1

∆2ky−k

f(x0, x1, x−1, ..., xk, x−k) = f(x−k, ..., x0, ..., xk) = (2k)!h2k

После замены x = x0 + th (x −xi = (t −i)h) первая формула Гаусса примет вид

L

(x

+ th) = y

+ t∆y

+

t(t − 1)

∆2y

−1

+

t(t − 1)(t + 1)

∆3y

−1

+

n

0

0

0

2!

3!

+

t(t2 − 1)(t − 2)

∆4y

−2

+ ... +

t(t2 − 1)(t2 − 22)...(t2 − (m − 1)2)(t − m)

∆2my

−m

,

4!

(2m)!

32

где t = (x − x0)/h.

Вторая формула Гаусса.

Вторая формула строится также как первая, только выбраны узлы

x0, x−1, x1, x−2, x2, .... Для таких узлов формула Ньютона с разделенными разностями имеет вид

Ln(x) = f(x0) + f(x0, x−1)(x − x0) + f(x0, x−1, x1)(x − x0)(x − x−1)+ +f(x0, x−1, x1, x−2)(x − x0)(x − x−1)(x − x1) + . . . +

+f(x0, x−1, x1, ..., x−m, xm)(x − x0)(x − x−1)(x − x1) . . . (x − x−m).

После той же замены x = x0 + th вторая формула Гаусса примет вид

t(t + 1)

2

Ln(x0 + th) = y0 + t∆y−1 +

∆ y−1+

2!

+t(t + 1)(t − 1)∆3y

−2

+ t(t2 − 1)(t + 2)

∆4y

−2

+ . . . +

3!

4!

+

t(t2 − 1)(t2 − 22) . . . (t2 − (m − 1)2)(t + m)

∆2my

−m

.

(2m)!

Формулы Гаусса используют конечные разности, лежащие в таблице конечных разностей вблизи горизонтали, проходящей через выбранный узел x0. Эти разности называются центральными.

Важно заметить еще раз, что различные интерполяционные многочлены, построенные для одного набора узлов, являются различными формами записи одного и того же многочлена.

3.9Оптимальный выбор узлов интерполяции

Если значения функции f(x) получаются с помощью трудоемкого расчета, то можно поставить вопрос о вычислении значений f(xi) в таких узлах xi [a, b], чтобы в оценке погрешности интерполяции

f(x) − Ln(x) = f(n)(ξ(x))ωn(x) n!

33

∏n

для многочлена ωn(x) = (x − xi) выполнялось условие

i=1

n

max ω

(x) = max

∏i

|

x

−

x

max

|

P (x) ,

a

x b

|

n

|

a

x b

=1

i| ≤ a x

b

|

≤ ≤

≤ ≤

≤ ≤

где Pn(x) = xn + an−1xn−1 + ... + a0 — произвольный многочлен степени n

с коэффициентом при старшей степени an = 1.

Такие наименее уклоняющимися от нуля многочлены существуют, они с точностью до множителя совпадают с многочленами Чебышева.

Многочлены Чебышева.

Многочлены Чебышева нулевой и первой степени имеют вид

T0(x) = 1, T1(x) = x,

а многочлены n - ой степени выписываются с помощью рекуррентной формулы

Tn = 2 x Tn−1 − Tn−2.

Легко показать (с помощью математической индукции), что T2n(x) —

четная функция, а T2n−1(x) — нечетная. Из рекуррентной формулы следует, что коэффициент при старшей степени Tn(x), n > 1 равен 2n−1.

На отрезке [−1, 1] многочлен Чебышева Tn(x) можно записать в виде

Tn = cos(n arccos x),

Отсюда следует, что на отрезке [−1, 1] у многочлена Tn(x) существует n

различных вещественных корней

xk = cos π(2k + 1), k = 0, 1, ..., (n − 1), xk [−1, 1], 2n

	и точек	π k
	x(k) = cos		, k = 0, 1, ..., n, x(k) [−1, 1],
		n

в которых многочлен Чебышева принимает экстремальные значения Tn(x(k)) = cos πk = (−1)k.

34

x [−1;1]

Рассмотрим многочлены Ten(x) = 21−nTn(x) с равными единице коэффициентами при старших степенях (при xn).

Лемма.

Если Pn(x) — произвольный многочлен степени n с коэффициентом при старшей степени равным единице, то

max |Pn(x)| ≥ max |Ten(x)| = 21−n.

x [−1;1] x [−1;1]

Доказательство. Предположим противное, пусть max |Pn(x)| < 21−n.

Степень многочлена Tn(x) − Pn(x) не выше n − 1 (старшие степени уни-

чтожаются). В силу

предположения, он не равен нулю тождественно. Если

e

Pn(x)

< 21−n для любого x [−1, 1], то знак разности Tn(x) − Pn(x) в

точках| |

экстремума многочлена Чебышева

e

sgn T

x(k)

P

x(k)

sgn

k

1−n

P x(k)

k, k

,

, ..., n

( en(

)−

n(

)) = (k)

((−1) 2

− n(

)) = (−1)

= 0 1

совпадает со знаком Tn(x

).

(x) меняет знак на отрезке [

Это означает, что

многочлен T

(x)

−

P

−

1, 1]

e

n

n

в

n + 1

– ой точке, то есть

имеет n корней. Отличный от нуля многочлен

e

степени не более n − 1 не может иметь n корней. Получили противоречие, лемма доказана.

Многочлены Чебышева
1		n−1	(x − cos	π(2k + 1)		), n = 1, 2, ...
		∏
T0 = √	2	, Tn(x) = 2n−1 k=0		2n

образуют на отрезке [−1, 1] ортонормированную с весом

√

2

систему

π

1 − x

2

многочленов, т.е.

1

= {

если n ̸= m,

∫

2

m

0,

π√

Tn(x) Tm(x) dx = δn

если n = m.

1

−

x2

1,

1

−

35

Чтобы получить наименее уклоняющийся многочлен на отрезке [a, b]

сделаем замену x = a + b + xeb − a, тогда, если xe [−1, 1], то x [a, b]. На

2 2

отрезке [a, b] выберем точки

x		=	a + b	+ x	b − a	,
					2
	k	2		ek

где xek = cos π(2k + 1), k = 0, 1, . . . , n − 1 [−1, 1] — корни многочлена

2n

Чебышева Tn(x). Для выбранных точек многочлен ωn(x) примет вид

n∏−1

ωn(x) = (x − xk) =

k=1

n−1

((

a + b

b − a

) −

(

a + b

b − a

π(2k + 1)

=

+ x

+

cos

=

2

2

2n

k=1

2

2

))

∏

(

b − a

n n−e1

π(2k + 1)

b − a

)

n T

=

x

−

cos

=

(x).

2

)

k=1

(

2n

) (

2

n

Это означает, что

∏

e

e e

max

ω

(x) =

b − a

n

max

T

(x) =

b − a

)

n

21−n = 21−2n(b

a)n

|

−

a≤x≤b |

n

|

(

2 )

−1≤x≤1

n

e

|

(

2

e

e

Если точки	a + b	+	b − a	cos	π(2k + 1)	взять в качестве узлов интерполя-
					2n
2		2

ции, то для соответствующего интерполяционного многочлена получится оценка погрешности

|f(x) − Ln(x)| ≤ Mn!n 21−2n(b − a)n,

где Mn = max |f(n)(x)|. Улучшить эту оценку за счет выбора любых дру-

a≤x≤b

гих узлов нельзя.

Замечание. На опасность появления большой погрешности интерполя-

ции в 1901г обратил внимание Рунге. На отрезке [−1, 1] рассматривалась

1

аналитическая функция f(x) = 1 + 25x2 (на рисунке изображен её график).

36

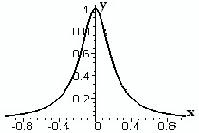
Рис. 2: Пример Рунге.

Если при построении интерполяционного многочлена для этой функции, выбрать равноотстоящие узлы, например, xk = ±k/n, k = 1, 2, . . . , n/2

(n– четное), то при n → ∞ последовательность Ln(x) не сходится к f(x)

для значений 0.73 ≤ |x| ≤ 1. Если же в качестве узлов выбирать корни полинома Чебышева, то Ln(x) → f(x) при n → ∞ для любого значения x [−1, 1].

Есть теорема Фабера: если f(x) непрерывно дифференцируема (одной непрерывности мало), то интерполяционные многочлены Ln(x), построенные на отрезке [−1, 1] по узлам, совпадающим с корнями многочлена Чебышева, сходятся к f(x) при n → ∞.

3.10Вопросы и упражнения для самоконтроля.

Вопросы

1.Сколько интерполяционных многочленов степени n−1 можно построить по заданным n узлам?

2.Сформулируйте постановку задачи интерполяции. Что такое экстраполяция?

3.Сформулируйте постановку задачи интерполяции с кратными узлами.

4.Как отличаются друг от друга различные интерполяционные многочлены (Лагранжа, Ньютона, и т.п.), построенные по одному и тому же набору узлов?

37

5.Как оценивается погрешность интерполяционного полинома? Как её можно уменьшить?

6.Как оптимальным образом выбрать узлы интерполяции?

7.Перечислите свойства разделенных разностей.

8.Перечислите свойства конечных разностей.

9.Для каких функций погрешность интерполяции равна нулю?

10.Пусть задана большая таблица значений функции. Как расположение значения х влияет на выбор интерполяционной формулы? Как наилучшим образом выбрать степень интерполяционного многочлена?

Упражнения

1. Пусть f(x) = sin πx2 , постройте интерполяционный многочлен P (x), совпадающий с функцией f(x) в точках x = 0, x = 1, x = 2. Оцените

|f(x) −P (x)| на отрезке [0, 2]. Сравните эту оценку с фактической погрешностью в точке x = 1/2 (или x = 3/2)

2.Пусть f(x) = sin 5x, x [0, 2π]. Определите шаг h таблицы значений f(x), чтобы линейная интерполяция (построение многочлена L2(x)) обеспечивала точность ε = 10−4.

3.Пусть на отрезке [0, π] заданы значения функции f(x) = sin x в узлах

xi, i = 0, 1, . . . , n (h = π/n). Определите, при каком значении числа n для интерполяционного многочлена Ln(x) будет выполняться оценка |f(x) −

Ln(x)| 6 10−2 для любого x [0, π].

√

4.На сетке xi, i = 0, 1, . . . , n, h = 5 0.05, заданы значения yi = T5(xi), где T5(x) — многочлен Чебышева. Вычислите значение ∆5y(0).

5.Постройте таблицу конечных разностей для таблицы значений функ-

ции

x	-3	-2	-1	0	1	2	3
y	0	-2.9	-4	-3.1	0	4.9	12

Многочленом какой степени разумно интерполировать эту функцию

38

6. Постройте интерполяционный многочлен Ньютона третьей степени для точки x = 2.7, если функция задана таблично

x	-3	-2	-1	0	1	2	3
y	0.1	-3	-4	-3.1	0	5.4	11.7

7. Пусть f(x) = sin x, P (x) и Q(x)- два полинома третьей степени, удо-

	k			k			k
влетворяющие условиям P (		)	= Q (		)	= f (		), k = 1, 2, 3, 4. Оцените
	3			3			3

для любого x [1, 10] значение |P (x) − Q(x)| .

8. Пусть дана таблица пятизначных десятичных логарифмов для x

[1, 10] с шагом h = 10−3. Будет ли погрешность линейной интерполяции

(многочлен L2(x)) меньше чем 5 · 10−5.

9. Постройте интерполяционный многочлен для функции Рунге f(x) =

1

1 + 25x2 , x [−1, 1]с помощью узлов xi = i/2, i = 0, ±1. Оцените погрешность.

10. Возьмите любой многочлен степени n > 3 вычислите его значения в n + 2 узлах. Используйте эти значения для построения интерполяционных многочленов степени n − 1, n и n + 1. Сравните полученные многочлены с

выбранным полиномом

11. Постройте кусочно-линейную функцию, соответствующую следую-

щим данным

x	0	1/6	1/3	1/2	2/3	5/6	1
y	1	4	1	-1	2	4	0

4Численное интегрирование

Во многих прикладных задачах возникает потребность в вычислении

интегралов вида

∫b

I(f) = ρ(x) f(x) dx,

(4.1)

a

39

где функция ρ(x), для которой существует явное выражение первообразной для xmρ(x) и любого целого m, называется весовой функцией (или весом). Смысл введения весовой функции будет понятен дальше, когда будут обсуждаться методы вычисления интегралов от сильно осциллирующих функций (у которых первая производная много раз меняет знак на

[a, b], см. стр. 60). Предполагается, что интеграл I(f) существует и функция f(x) имеет столько непрерывных производных, сколько требуется.

Иногда такие интегралы удается вычислить аналитически, либо вручную, либо с помощью машинных символьных систем, иногда так не получается, и интегралы приходится вычислять приближенно с помощью квадратурных формул. Формулы для приближенного вычисления интегралов (квадратурные формулы) строятся с помощью аппроксимации функции f(x) некоторой другой функцией g(x), интеграл от которой вычисляется сравнительно просто. Для аппроксимации f(x) может быть использован любой класс простых функций, таких как полиномы, сплайны (кусочнополиномиальные функции), тригонометрические, экспоненциальные или логарифмические функции. Конкретный выбор класса аппроксимирующих функций зависит от свойств подынтегральной функции.

Наиболее часто для вычисления I(f) используются квадратурные формулы, которые строятся с помощью интерполяционных многочленов. Такие формулы имеют вид

		b		b − a	n
	I(f) =	ρ(x) f(x) dx S (f) =				C f(x )
					∑
	a		≈ n	2		k k
	∫				k=1

где xk [a, b] (k = 1, 2, ..., n) – узлы, а Ck – коэффициенты квадратурной формулы.

Очевидно, что для достижения заданной точности при вычислении I(f)

с помощью квадратурной формулы Sn(f), требуется знать оценку погреш-

40