Schisla_1

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение высшего

профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

С. Н. Овчинникова

Численные методы

Часть I

Численные методы математического анализа

Курс лекций

2007 год

Содержание

1	Введение		3
2	Вычислительная погрешность при расчетах на вычислительных маши-
	нах		10
	2.1	Математические особенности машинной арифметики . . . . . . . . . . . .	10
	2.2	Числа с плавающей запятой . . . . . . . . . . . . . . . . . . . . . . . . . .	11
	2.3	Суммарный эффект ошибок округления . . . . . . . . . . . . . . . . . . .	13
	2.4	Пример неустойчивого алгоритма . . . . . . . . . . . . . . . . . . . . . . .	17
3	Полиномиальная интерполяция		18

3.1Постановка задачи линейной интерполяции. . . . . . . . . . . . . . . . . . 19

3.2Полиномиальная интерполяция. . . . . . . . . . . . . . . . . . . . . . . . . 20

3.3 Интерполяционный многочлен Лагранжа . . . . . . . . . . . . . . . . . . 21

3.4Интерполяционный многочлен Ньютона. . . . . . . . . . . . . . . . . . . . 24

3.5Интерполирование с кратными узлами (постановка задачи) . . . . . . . . 28

3.6Интерполяционные многочлены для равноотстоящих узлов . . . . . . . . 28

3.7Интерполяционные формулы Ньютона для равноотстоящих узлов . . . . 30

3.8Интерполяционные формулы Гаусса . . . . . . . . . . . . . . . . . . . . . . 32

3.9	Оптимальный выбор узлов интерполяции . . . . . . . . . . . . . . . . . .	33
3.10	Вопросы и упражнения для самоконтроля. . . . . . . . . . . . . . . . . . .	37
4 Численное интегрирование		39

4.1Формулы Ньютона - Котеса . . . . . . . . . . . . . . . . . . . . . . . . . . 41

4.2Формулы типа Гаусса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

4.3Составные (обобщенные) квадратурные формулы . . . . . . . . . . . . . . 53

4.4 Практическая оценка погрешности (правило Рунге) . . . . . . . . . . . . 58

4.5Алгоритм вычисления интеграла с автоматическим выбором шага . . . . 59

4.6Вычисление интегралов от сильно осциллирующих функций . . . . . . . 60

4.7Вопросы и упражнения для самоконтроля. . . . . . . . . . . . . . . . . . . 63

5 Численное дифференцирование

63

5.1Вывод формул численного дифференцирования с помощью интерполяции 64

5.2Метод неопределенных коэффициентов . . . . . . . . . . . . . . . . . . . 66

5.3О вычислительной погрешности численного дифференцирования . . . . . 69

2

Цель вычислений в проникновении в суть, а не в цифрах.

Цель расчетовпонимание, а не числа.

Р. Хемминг.

1Введение

Всвязи с общедоступностью вычислительной техники настоящее время характерно снижением интеллектуального уровня задач, требующих внимания математиков, в частности специалистов в области численных методов. Однако, теория численных методов, однажды возникнув, развивается по своим внутренним законам так же, как и другие фундаментальные разделы математики.

Снижение общей математической образованности и общедоступность вычислительной техники делают необходимым создание комплексов программ, допускающих их использование исследователями невысокой математической квалификации. Разработка даже таких комплексов невозможна без дальнейшего развития теории численных методов. Специалисты в области теории численных методов и практики их применения будут неминуемо востребованы в процессе развития промышленности и науки.

Эффективным методом исследования многих задач является вычислительный эксперимент – технология исследования сложных проблем, основанная на построении и анализе с помощью ЭВМ математических моделей изучаемого объекта.

Рассмотрим эту технологию. С чего начинается исследование?

1. Первый шаг — это накопление наблюдений о свойствах изучаемого объекта и зависимости между ними. На этом шаге выделяются основные факторы, которые следует учитывать при изучении объекта. Например, в физике эти факторы связаны с законами сохранения. Этот раздел исследования подвластен специалистам в области знаний, которой принадлежит

3

изучаемый объект.

2.Второй шаг — формализация изучаемой проблемы, т.е. построение соответствующей математической модели. Для этого после выделения наиболее существенных свойств изучаемого объекта требуется описать с помощью математических соотношений основные зависимости между ними. Очевидно, что построение такой математической модели является неизбежным компромиссом между учетом всех факторов, играющих роль в данной задаче, и созданием модели достаточно простой, чтобы ее можно было решить имеющимися средствами. В науке 19 и начала 20 веков рассматривались модели явлений, решения которых находились вручную: либо аналитически, либо численно. С появлением ЭВМ, увеличением их мощности и развитием численных методов стало возможно работать со все более сложными моделями.

3.Третий шаг — преобразование математической модели в такую (дискретную модель), чтобы можно было построить упорядоченную последовательность действий, приводящих к результату. Это требуется для решения поставленной задачи с помощью вычислительной техники.

4.Четвертый шаг — разработка алгоритма расчета приближенного решения дискретной модели, составление и тестирование программы, реализующей этот алгоритм на вычислительной технике.

5.Наконец, требуется провести расчеты, проанализировать результаты,

иубедиться, что они соответствуют изучаемому явлению, т.е. мало отличаются от результата, соответствующего построенной математической модели (понятие ”мало” будем пояснять для каждой рассматриваемой задачи),

исогласуются с наблюдениями.

Схема вычислительного эксперимента изображена на рис. 1.

Если результаты вычислений и результаты наблюдений сильно различаются, то это может быть связано с неправильной постановкой задачи (пункт II.). Кроме того, возможны ошибки в программе, что исключается,

4

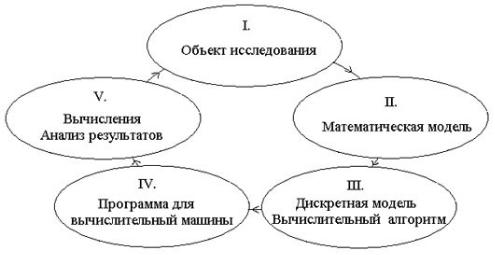
Рис. 1: Cхема вычислительного эксперимента.

если она хорошо оттестирована, и ошибки вычислений.

Cуществуют два главных источника ошибок (несогласованности с экспериментом):

1)неизбежные погрешности самой модели,

2)неизбежные ошибки численного решения.

Если несогласованность с натурными исследованиями связана с построением модели, то иногда ее приходится модифицировать (учитывать новые факторы или новые связи между ними), а иногда требуется полный пересмотр модели и подход к изучению явления с совершенно других позиций.

Ошибки же численного решения связаны с ошибками выбранного численного метода (ошибки дискретизации) и с ошибками округления, которые вызваны тем, что в памяти вычислительной машины существует конечное количество чисел, каждое из которых содержит конечное число цифр.

Раздел III схемы вычислительного эксперимента является предметом изложения курса "Методы вычислений".

Может возникнуть вопрос, зачем надо изучать столь подробно численные методы, для большинства из которых существуют хорошо зарекомендовавшие себя, реализующие их программы и вычислительные системы.

5

Однако сознательное использование этих программ и систем и, тем более, создание новых улучшенных версий вряд ли возможно без изучения самих методов и связанных с ними теоретических представлений. Кроме того, большинство стандартных программ мало устойчиво к ошибкам пользователей и обеспечивает уровень диагностики явно недостаточный для неподготовленного пользователя.

Предмет "Численные методы" имеет некоторые особенности:

1.для численных методов характерна множественность — одну и ту же задачу можно решить различными методами;

2.вновь возникающие естественно - научные задачи и быстрое развитие вычислительной техники вынуждает пересматривать известные методы и алгоритмы и создавать новые.

Эти особенности предмета, его обширность и неоднородность делают иллюзорной попытку изложить предмет ”во всей полноте и строгости”. В курс лекций входит минимальный материал, достаточный для дальнейшей работы выпускников Университета в области применения и создания вычислительных методов. Хотелось бы, чтобы при рассмотрении различных методов, испытанных практикой и успешно применяемых при решении реальных задач, сформировалась идеология подхода к численному решению задач.

Вычислительный алгоритм

При рассмотрении математической модели сначала предпринимается попытка получить точное решение. Обычно такое решение можно найти при определенном (часто радикальном) упрощении задачи. Такие упрощенные постановки с известными решениями полезны как контрольные варианты для более общей исходной задачи.

Если точное решение найти невозможно, то разыскивается численный метод для вычисления приближенного решения.

При выборе численного метода учитываются доступные вычислитель-

6

ные средства и программное обеспечение. Однако существуют общие, неза-

висимые свойства методов, алгоритмов и расчетов на ЭВМ, о которых нель-

зя забывать.

1.B машинной арифметике все действия выполняются с числами, имеющими конечное число цифр, а это означает, что неизбежны ошибки округления. Требуется построить вычислительный алгоритм так, чтобы ошибки округления не накапливались и не искажали результат.

2.Замена исходной математической модели дискретной, как правило, вносит неустранимую ошибку — ошибку дискретизации, и численный метод, выбранный для решения дискретной модели, также вносит ошибку — ошибку метода.

3.Вычислительный алгоритм, построенный для реализации расчета приближенного решения, может оказаться неустойчивым, т.е. малым ошибкам входных данных будут соответствовать большие ошибки результата. Примером такого неустойчивого алгоритма является вычисление In =

1	xnex−1 dx с помощью рекурентной формулы In = 1 − nIn−1, для n =
0
∫		(см. стр. 17).
1, 2, ..., N

4. Вычислительный алгоритм должен быть эффективным, т.е. коли-

чество человеческих усилий и ресурсов вычислительной машины, необходимых для решения задачи, должно быть минимальным.

Итак при выборе метода решения математической модели надо помнить:

1.об ошибках округления;

2.об ошибке метода;

3.об устойчивости алгоритма;

4.об эффективности метода.

Несколько слов о качестве составляемых программ. Вот некоторые критерии качественного программирования вычислительных задач:

1. надежность — программа не содержит ошибок и вычисляет именно то, ради чего составлена;

7

2.работоспособность — программа может обнаруживать неверные данные и обстоятельства, при которых нельзя ожидать правильных результатов, фиксировать разные неформальные ситуации, и обрабатывать их так, чтобы это удовлетворяло пользователя;

3.переносимость — программа может быть перенесена с одной ВМ на другую с минимальными усилиями и без потери надежности (любая используемая характеристика конкретной ВМ, как, например, длина слова, четко выделяется);

4.поддерживаемость — программа должна быть составлена так ясно

илогично, чтобы в нее легко было вносить изменения с минимальной вероятностью порождения новых ошибок, программа должна быть хорошо документирована.

Пример. Рассмотрим процесс создания математической модели на примере исследования естественных взаимоотношений в природе типа хищник - жертва (волки и кролики, паразиты и организмы, на которых они паразитируют).

Пусть в момент времени t количество жертв(кроликов) – x(t), а хищников(волков) – y(t), и пусть:

1.норма рождаемости жертв (% рождаемости) – xr, норма естественной смертности жертв (от старости и болезней) – xs (очевидно, xr > xs, т.е.

α= xr − xs > 0);

2.число случаев, когда хищник убивает жертву, зависит от вероят-

ности их встречи, т.е. пропорционально числу жертв и числу хищников c

коэффициентом β < 0;

3.при отсутствии жертв число хищников по естественным причинам (не хватает пищи) убывает, т.е. скорость изменения числа хищников пропорциональна их числу с коэффициентом γ < 0;

4.в результате встреч с жертвами число хищников растет пропорционально xy с коэффициентом δ > 0.

8

Все коэффициенты α, β, γ и δ считаются известными величинами, по-

лученными, например, из обработки результатов наблюдений.

Из первых двух предположений следует

dxdt = αx + βxy,

а из следующих двух

dydt = γy + δxy.

Таким образом, построена система дифференциальных уравнений, опи-

сывающая межвидовые отношения типа хищник - жертва

dxdt = αx + βxy, dydt = γy + δxy.

Эти уравнения были выведены в 1925 г. и известны как уравнения ЛоткиВольтерра. Чтобы выделить одно решение построенных уравнений, требуется задать дополнительные условия, например, начальные

x = x0, y = y0, при t = 0

Построена модель, как ее использовать? Только в исключительных случаях удается найти решение математической модели в явном виде. Иногда утверждение "задача решена" означает, что доказана теорема существования и единственности. Ясно, что этот важный результат недостаточен для практических приложений. Необходимо изучить поведение решения и найти те или иные количественные характеристики.

Для дальнейшего изучения рассматриваемой модели надо найти численный метод решения полученной задачи Коши.

Если решение разыскивается на отрезке 0 6 t 6 T , то можно на этом отрезке выбрать систему точек (сетку) tn = nτ, n = 0, 1, 2, . . . , N, τ = T/N

и вычислить приближенные значения решения un ≈ x(tn), vn ≈ y(tn) в

этих точках (узлах сетки).

9

Используя приближенное равенство
	dx	(t	)	≈	x(tn) − x(tn−1)
	dt	n−1			τ

получим для вычисления un и vn дискретную модель

un − un−1 = αun−1 + βun−1vn−1

τ

vn − vn−1 = γvn−1 + δun−1vn−1

τ

Полученная система нелинейных уравнений относительно un и vn легко решается. Действительно, зная u0 и v0, легко вычислить u1 и v1 и т.д.

При расчете требуется заботиться о том, чтобы неизбежные погрешности

округлений не искажали результат.

Очевидно, даже такой простой расчет при больших N и нескольких

наборах параметров (α, β, γ, δ) лучше поручить ЭВМ.

2Вычислительная погрешность при расчетах на вычислительных машинах

2.1Математические особенности машинной арифметики

Машинная арифметика имеет свои характерные особенности. Правильно учитывая их, можно достичь высокой точности в решении задач на

вычислительных машинах.

Вспомним определения абсолютной и относительной погрешностей. Пусть

x - точное значение некоторого числа, а x его приближенное значение.

Определение: Наименьшее из известных чисел ∆x таких, что |x − x | ≤

∆x называется абсолютной погрешностью числа x.

Определение: Отношение абсолютной погрешности ∆x числа x к его модулю (или к модулю его приближенного значения x ) называется отно-

сительной погрешностью числа x
δ(x) =	∆x			(или	δ(x) =	∆x			).
		x	|				x	|
|					|

10