_Глава 5 Лин алг

1

Введение в Maple

для студентов - физиков

Глава 5. Линейная алгебра

При решении физических задач линейная алгебра - это искусство использования матриц и векторов.

Рассматриваемые в главе вопросы/задачи

Сложение матриц	Adding matrices
Угол между двумя векторами	Angle between vectors
Вихрь	Curl
Детерминант	Determinant
Дивергенция	Divergence
Собственные функции и собственные	Eigenvalues and eigenvectors
значения	Gradient
Градиент
Инвертирование матриц	Invert a matrix
Лапласиан	Laplacian
Создание матриц	Making matrices
Создание векторов	Making vectors
Умножение матриц, векторов	Multiplying matrices, vectors
Норма или амплитуда	Norm or magnitude
Произведения: скалярное, векторное	Products: dot and cross
Вращение матриц	Rotation matrices
Команды Row и Column	Row and Column Commands
Система линейных уравнений	System of linear equations
След	Trace
Транспонирование	Transpose

Определение (задание) матриц и векторов Сложение, вычитание, умножение Инверсия, детерминант, норма и т.п. Решение систем линейных уравнений

Векторы: скалярное и векторное произведения Собственные значения и собственные векторы Векторные вычисления: grad, div, curl (rot)

Плотность заряда ρ и плотность тока j статического электрического и магнитного полей для различных объектов из уравнений Максвелла

Электростатический потенциал точечного диполя.

	2
Упоминаемые в главе команды Maple
with(LinearAlgebra)		DotProduct,
Matrix		CrossProduct,
Vector		VectorAngle
Column		transpose
Row		Gradient
<...>		Divergence
Evalf		Curl
evalm		Laplacian
&*		SetCoordinates
Add		cartesian
MatrixInverse		cylindrical
Determinant		spherical
Transpose
HermitianTranspose
Trace
Norm
LinearSolve

Сведения о линейной алгебре можно получить в запросе ?LinearAlgebra.

Прежде чем действовать, следует вызвать пакет:

> with(LinearAlgebra):

3

Матрицы, векторы и основные операции

Определение (задание) матриц и векторов

Первое, что вам надо знать: как создавать матрицы и векторы.

В Maple для этого есть много способов, но рекомендуется близкий к тому, как делается в MatLab.

Для создания матрицы А 2x2 , содержащей 1,2,3,4 надо:

> A:=Matrix([[1,2],[3,4]]);

Для ссылок на элементы матрицы надо использовать обозначения в виде

A[row,column], т.е. A[1,2] :

> A[1,2];

Если вы хотите только определить матрицу В 2x2 , но не присваивать ей значения, надо написать:

> B:=Matrix(1..2,1..2);

Как только В определена, присвоить ей значения можно любым способом, в том числе и вручную

> B[1,1]:=2;B[1,2]:=3;B[2,1]:=7;B[2,2]:=4;

Можно посмотреть на В, чтобы удостовериться, что все правильно:

> B;

Детали - см в команде Matrix ,задав ?Matrix.

Можно создать векторыстолбцы или строки с помощью команды Vector :

По умолчанию создается векторстолбец

> b:=Vector([5,6]);

Для создания вектора-строки (row) , надо сказать об этом Maple'у

> b:=Vector[row]([5,6]);

Если хотите заполнить векторы числами из строк или столбцов матрицы - используйте команды Column и Row .

Например, чтобы заполнить с вторым столбцом матрицы А надо написать:

> c:=Column(A,2);

Для заполнения с первой строкой А:

> c:=Row(A,1);

Вот еще удобный способ для определения матриц и векторов-столбцов. Вектор-столбец можно определить без специальной команды, с помощью

4

синтаксической конструкции Column Row <...> :

> s:=<1,2,3>;

А поскольку матрица представляется как набор векторов-столбцов, то и матрицу можно определить таким же способом:

> R:=<<1,2,3>|<4,5,6>|<7,8,10>>;

Об этой форме представления надо знать, поскольку она часто используется в Maple help .

Еще способ определения матриц в Maple - палитра слева от рабочего листа Matrix Palette. Использование элементов интерфейса достаточно очевидное, термины, в основном, понятны (на всякий случай: skew symmetric - кососимметрическая). Установите курсор в пустую группу ниже (лучше делайте это на отдельном листе, как обычно) и выберите нужные опции в окне палитры. Можно вручную заполнить элементы матрицыm[x,x] , можно использовать шаблон для матриц определенного вида.... После этого она готова для присваивания с помощью :=.

В Maple, вам не надо работать только с числами. Матрицы и векторы могут содержать формулы:

>d:=Matrix([[x11,x12],[x21,x22]]);

или

>e:=Matrix([[x^2*y,y*x],[sin(x),1/x]]);

Теперь предположим, что надо задать значения х и у и затем посмотреть на матрицы в представлении с плавающей запятой.

>x:=1;y:=2;

>e;

Это уже было, и мы знаем, что делать - примените evalf:

> evalf(e);

Не получилось...

Проблема в том, что е - это не выражение , а матрица выражений, поэтому Maple'у нужны две команды eval: evalm внутри, чтобы сослаться непосредственно на элементы е и evalf снаружи, чтобы запустить расчеты с плавающей запятой.

> evalf(evalm(e));

Спросите ?evalm, чтобы увидеть о чем эта команда, или

запомните, что для получения численного ответа, надо применять десятичные точки в числах

5

Описание команды evalm (из справки)

Функция evalm вычисляет выражения, включая матричные. Она выполняет суммирование, умножение, возведение в целую степень , в том числе для матриц и показывает отображение функций на матрицы.

Учтите, что прежде чем передавать аргументы в evalm, Maple может выполнить упрощения, и эти упрощения будут действительны для матриц. Например, evalm(A^0)возвратит 1, а не единичную матрицу.

Неприсвоенные имена будут рассматриваться как либо символьные матрицы или скаляры, в зависимости от их использования в выражении.

Для обозначения некоммутативного умножения матриц, используйте оператор &*. Произведение матриц ABC может быть введено как A &* B &* C , или как &*(A,B,C), причем последнее более эффективно. Применяется автоматическое упрощение, такое как сбор констант и степеней. НЕ ИСПОЛЬЗУЙТЕ *чтобы обозначить чистое умножение матриц, поскольку этовернетошибку. Опреандами &*должны быть матрицы(или имена) за исключением 0. Невычисленное произведение матриц рассматривается как матрицы. Оператор &*имеет то же старшинство, что и оператор * .

Используйте 0чтобы обозначить нулевой скаляр или матрицу. Применяйте &*()для обозначения единичной матрицы (?). Возможно, удобно применять alias(Id=&*()).

Если в сумме есть матрица и константа, то Maple рассматривает константу, как умноженную на единичную матрицу. Следовательно, матричные полиномы можно вводить в точности так, как скалярные полиномы.

Сложение, вычитание, умножение

> restart:with(LinearAlgebra):

Есть много способов выполнения этих алгебраических операций в Maple, но показан будет только один. Остальные - см. ?LinearAlgebra

Для сложенеия двух матриц В+С 3x3 используйте команду Add или просто знак +

>B:=Matrix([[1,2,3],[4,5,6],[7,8,9]]);

>C:=Matrix([[3,2,1],[5,6,4],[9,7,8]]);

>E:=Add(B,C);

или

> E:=B+C;

Вычисление сводится к сложению с матрицей со знаком минус

>E:=Add(B,-C);

или

>E:=B-C;

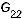
6

Очень внимательно следите за тем, чтобы сложение и вычитание имели смысл. Например,

>F:=Matrix([[5,7],[1,3]]);

>Add(E,F);

поскольку матрицы не одинакового размера.

Умножение матриц - с помощью команды Multiply :

> G:=Multiply(B,C);

Есть хороший способ умножения матриц , который можно найти в списке команд по запросу ?LinearAlgebra.

Задача5.1
Проверьте ручным счетом, что Maple правильно рассчитывает	.

--------------------------------------------------------------------------------------------------

Можно умножать матрицы и векторы так:

>b:=<5,6,7>;

>Multiply(B,b);

Как и ожидалось, умножение квадратной матрицы на вектор-столбец дает вектор-столбец. Умножение вектора-строки на квадратную матрицу дает новый вектор-строку:

> c:=Vector[row]([1,2,3]);

(или в сокращенной форме)

>c:=<1|2|3>;

>Multiply(c,C);

Можно умножать матрицы и векторы на скаляры простым оператором умножения

>3*b;

>5*B;

Здесь не говорится о делении. Это сложная процедура , о которой позже расскажем разделе "Решение систем линейных уравнений".

Задача 5.2

Важным применением умножения матриц является вращение векторов в трехмерном пространстве. Аккуратно нарисованная картинка и тригонометрия покажут, что если вектор v поворачивается против часовой стрелки вокруг оси х на угол θ (если смотреть в направлении начала координат по оси х), то новый вектор задается матрицей Rx, умноженной на v где Rx задается так:

> Rx:=Matrix([[1,0,0],[0,cos(theta),-sin(theta)],[0,sin(theta),cos(theta)]]);

Norm(v,2).

7

Подобно этому получается вращение матриц вокруг осей y- и z- на углы φ и ψ:

>Ry:=Matrix([[cos(phi),0,sin(phi)],[0,1,0],[-sin(phi),0,cos(phi)]]);

>Rz:=Matrix([[cos(psi),-sin(psi),0],[sin(psi),cos(psi),0],[0,0,1]]);

(Замечание: в знаках матрицы Ry нет ошибки. Иной знак, чем в Rx и Rz - из-за того, что вращение полностью определяется правилом правой руки для углов: направьте большой палец руки по направлению оси вращения, а остальные пальцы крутите в направлении положительных углов. Сделайте это для φ =π/2 и проверьте, что Ry - правильное.)

Используйте эти матрицы вращения чтобы проверить где заканчивается вектор [1,0,0] после последовательности поворотов:

(a)на 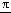относительно оси у, затем

(b)на 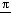относительно оси х, и в конце

(c) на		относительно оси z.

После получения ответа в Maple , проверьте его "на пальцах". (Удостоверьтесь, что координатные системы - правые).

Затем возьмите тот же вектор [1,0,0], но выполните действия (вращения) в обратном порядке.

Получилось ли то же самое?

(Нет, - по причине того, что операции вращения не коммутативны.)

Вращение не должно изменять модуль вектора. А получилось ли это у нас? Модуль вектора v можно получить командой

Инверсия, детерминант, норма и т.п.

Maple допускает множество действий с матрицами. Посмотреть список возможностей можно по запросу ?LinearAlgebra .

Далее рассмотрены несколько встречающихся в физике тем .

Определим матрицы

>restart:with(LinearAlgebra):

>B:=Matrix([[1,2,3],[4,5,6],[7,8,9]]);

>C:=Matrix([[3,2,1],[5,6,4],[9,7,8]]);

MatrixInverse: Для получения обратной матрицы, скажем, С делают так:

> MatrixInverse(C);

8

Для проверки делают так:

> Multiply(C , MatrixInverse(C));

Determinant: Получить детерминант матрицы можно так:

> Determinant(B);Determinant(C);

Transpose: транспонирование матрицы получается заменой строк на столбцы, подразумевая отражение матрицы относительно главной диагонали. Имеет смысл также транспонирование не квадратной матрицы.

>Transpose(C);

>E:=Matrix([[1,2,3]]);

>Transpose(E);

В квантовой механике вам понадобится брать транспонированную комплексно сопряженную матрицу, которую называют эрмитово сопряженной (эрмитово транспонированной) HermitianTranspose:

>F:=<<1,I>|<2*I,2>>;

>HermitianTranspose(F);

Trace: след - это сумма диагональных элементов матрицы.

> Trace(C);

Norm: Норма вектора имеет много определений. Вы привыкли брать квадраты элементов, складывать их и вычислть квадратный корень из результата сложения. Это определение используется (почти) только в физике, но Maple умнее и берет корень k-го порядка из суммы k- ых степеней элементов. Для физики k=2:

> Norm(E,2);

Норма матриц сложнее - см.запрос ?LinearAlgebra[Norm].

Задача 5.3

Найдите матрицу , обратную определенной в этом разделе матрицы В. Объясните, почему вместо ответа получилось сообщение об ошибке.

9

Решение систем линейных уравнений

Maple знает как решать эту задачу:

(задание простое - потренируйтесь в английском)

There are three friends, Alice, Bob, and Chuck. The sum of Alice's and Bob's ages are 1.5 times Chuck's age. Chuck's age minus Bob's age is 6. Alice's age added to Chuck's age is 2.25 as large as Bob's age. If Bob used to date Alice, but is now far away in a foreign country, and if Chuck thinks Alice is really cute, is Bob in big trouble? The mathematical part of this problem is just a problem in linear algebra of the form A*x = b, with the ages in the order [Alice, Bob, Chuck]. Here are A and b:

>restart;with(LinearAlgebra):

>A:=Matrix([[1,1,-3/2],[0,-1,1],[1,-2-1/4,1]]);

>b:=Vector([0,6,0]);

Нам надо решить относительно вектора x , составленного из возрастов трех друзей. В Maple есть команда LinearSolve ,которая делает эту задачу простой:

> LinearSolve(A,b);

так можно решить любую линейную систему. Позже мы посмотрим, как можно применить команду solve для решения уравнений.

Задача 5.4
Рассмотрим 5 пружин с постоянными упругости	, сцепленных друг с

другом по оси x в указанном порядке. В несжатом состоянии длины пружин равны

соответственно	.
Найдите длины пружин	, когда они растянуты так, что сумма их длин

вдвое больше суммарной длины в нерастянутом состоянии.

После того, как Maple даст общее алгебраическое решение задачи (несколько жутковатое), получите численный ответ, считая, что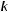

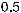
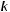
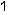
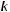
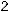
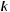
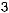
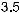
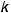
. Пусть длина каждой пружины в нерастянутом состоянии одинакова и равна 10 cм. Сила действующая на пружину дается формулой 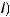. Понадобятся навыки решения задач на равновесие из механики 1-го курса.

10

Векторы: скалярное и векторное произведения

Maple знает, как выполнять скалярное произведение, векторное произведение и как находить угол между двумя векторами с помощью команд DotProduct,

CrossProduct, и VectorAngle.

>restart:with(LinearAlgebra):

>v1:=<1|2|3>;v2:=<4|5|6>;

>DotProduct(v1,v2);CrossProduct(v1,v2);

Здесь все что надо.

>VectorAngle(v1,v2);

Или еще,

>evalf(VectorAngle(v1,v2));

Учтите, что выдача - в радианах.

Собственные значения и собственные векторы

Одно из наиболее важных применений линейной алгебры в физике - это собственные значения и собственные векторы. Они появляются в классической механике, математической физике, квантовой механике, численном анализе.

В применении к матрицам задача о собственных значениях выглядит так:

Дана квадратная матрица A. Какими должны быть векторы xj и числа λj , чтобы при умножении A на xj получался вектор xj, умноженный на число λj

Существуют ли такие xj и λj, что можно записать:

A xj =λj xj

Поскольку умножение матрицы на вектор одновременно вращает вектор и умножает его на число, неясно, есть ли решение у этой задачи. Но математически можно доказать, что в большинстве случаев, для матрицы размером NxN есть N таких векторов и значений, (они и называются собственными значениями и собственными векторами). Зачастую - это комплексные величины , которые, как кажется, не имеют физического смысла, но даже если так, физический смысл с их помощью (или из них) можно получить. Если собственные значения - действительные, то собственные векторы обладают очень особым свойством: