•Определим вероятность ошибочного приема сообщения. Пусть p – вероятность появления ошибки при передаче отдельного бита кодовой комбинации. Для оценки вероятности возникновения ошибки при передаче кодовой комбинации, состоящей их n бит необходимо принять определенные исходные предположения, которые называются математической моделью ошибок.
•Наиболее простая из них (рассмотрим только ее) – считать появление ошибки в каждом отдельном знаке (бите) кода случайным событием, которое не зависит от того, с ошибками или без них были переданы предыдущие биты. Тогда:
•1 – p – вероятность безошибочной передачи отдельного бита;
•(1 – p)n – вероятность безошибочной передачи цепочки n бит;
•Pn = 1 – (1 – p)n – вероятность появления хотя бы одной ошибки в
комбинации n бит. При малых p можно воспользоваться соотношением Бернулли; тогда Pn ≈ n∙p. Так можно оценить суммарную вероятность появления всех ошибок.
•Если же требуется найти вероятность ошибки с заданной кратностью t, то следует воспользоваться формулой биноминального распределения:
Pn Cnt pt (1 p)n t
•Вероятность ошибочной передачи сообщения с учетом всех ошибок кратности от 1 до t находится так:
t
Pn Cni pi (1 p)n i
i 1
Связь между корректирующей способностью кода и кодовым расстоянием
•Важная характеристика помехоустойчивого кода – наименьшее
расстояние между разрешенными кодовыми комбинациями dmin. Оно обеспечивает корректирующие свойства кода.
•Определить минимальное кодовое расстояние между разрешенными комбинациями сообщений разведчиков.
•Ответ: dmin = min {6, 5, 5} = 5.
•Проиллюстрируем этот подход для (3,2)-кода: количество информационных разрядов
k = 2, следовательно, число разрешенных кодовых комбинаций Sр = 22 = 4; общее число кодов S=23 =8. Число проверочных бит r = n – k = 1 и устанавливать их значение условимся таким образом, чтобы количество «единиц» во всех кодовых комбинациях было бы четным (по этой причине такой проверочный бит называется битом четности).
Ui |
a1 |
a2 |
b |
|
U1 |
0 |
0 |
0 |
0 |
U2 |
0 |
1 |
1 |
2 |
|
|
|
|
|
U3 |
1 |
0 |
1 |
2 |
|
|
|
|
|
U4 |
1 |
1 |
0 |
2 |
|
|
|
|
|
Будем обозначать разрешенные кодовые комбинации Ui. Их
информационная часть может принимать значения 00, 01,10 и 11 (обозначим эти биты a1 и a2); проверочный бит b принимает значения,
приведенные в таблице. Последняя колонка содержит суммы (количество) бит со значением "1" в каждой кодовой комбинации. Любую из 8 существующих для n = 3 кодовых комбинаций можно считать вектором в пространстве, построенном на единичных векторах a1, a2, b –
это иллюстрируется рисунком.
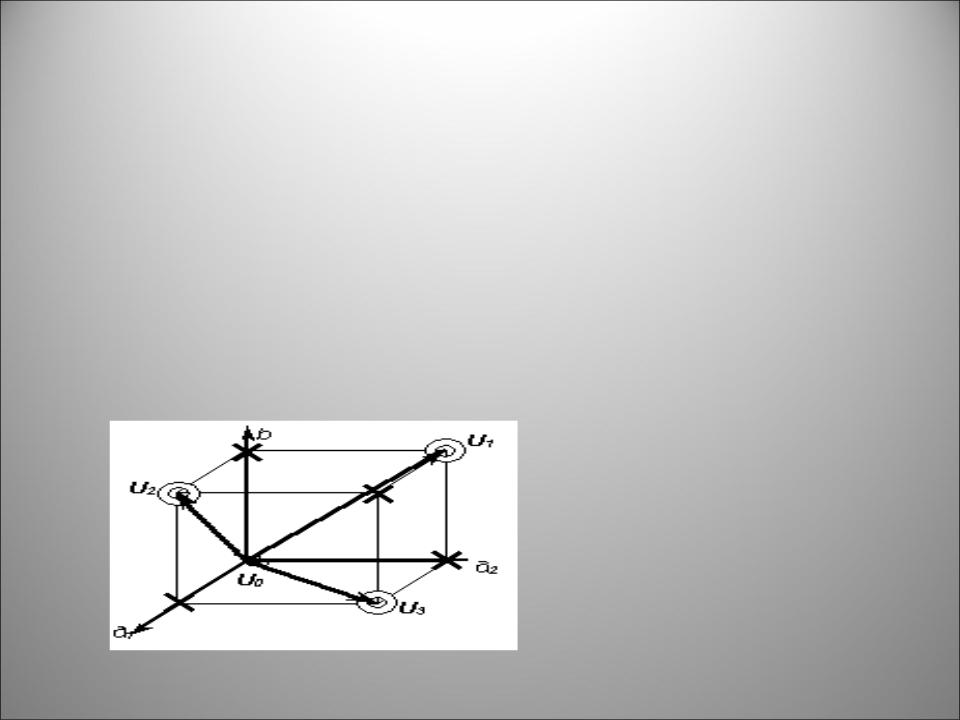
•Отметим разрешенные комбинации ноликами; остальные, очевидно, будут запрещенными - их отметим крестиками. Видно, что минимальное кодовое расстояние между разрешенными комбинациями равно 2 (расстояние между разрешенными вершинами по ребрам куба). На рисунке однократной ошибке соответствует переход из вершины куба в соседнюю вершину. Любая однократная ошибка переводит разрешенную комбинацию в запрещенную, следовательно, может быть обнаружена. Однако исправить такую ошибку нельзя, поскольку в любую из запрещенных вершин за один шаг можно попасть, по крайней мере, из двух разрешенных.
Квопросу о связи кодового расстояния и корректирующей способности кода.
•Обобщим рассуждения. Пусть необходимо построить код, обнаруживающий все ошибки кратности τ и меньше. Построить такой
код – это значит из множества S возможных комбинаций выбрать Sp разрешенных комбинаций так, чтобы любая сумма по модулю 2 с любым вектором ошибок с весом ω ≤ τ не дала бы в результате никакой другой разрешенной комбинации. Для этого необходимо, чтобы наименьшее кодовое расстояние удовлетворяло условию
dmin 1
•Сможет ли командир обнаружить двукратную ошибку?
•Ответ: да, потому что 5 ≥ 2+1.
•Рассмотрим код со значностью n=3. Все возможные комбинации этого кода приведены в таблице:
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
|
|
|
|
|
|
|
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
|
|
|
|
|
|
• Составим матрицу кодовых расстояний:
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
А1 |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
А2 |
1 |
0 |
2 |
1 |
2 |
1 |
3 |
2 |
А3 |
1 |
2 |
0 |
1 |
2 |
3 |
1 |
2 |
|
|
|
|
|
|
|
|
|
А4 |
2 |
1 |
1 |
0 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
А5 |
1 |
2 |
2 |
3 |
0 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
А6 |
2 |
1 |
3 |
2 |
1 |
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
А7 |
2 |
3 |
1 |
2 |
1 |
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|
А8 |
3 |
2 |
2 |
1 |
2 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
•Для того, чтобы код обеспечивал обнаружение однократных ошибок, необходимо из 8 возможных комбинаций выбрать в качестве разрешенных такие, расстояние между которыми было бы не менее d=2. Например, определим разрешенными комбинациями такие:
•А2 = 001, А3 = 010, А5 = 100, А8 = 111. Любая однократная ошибка переводит разрешенную комбинацию в запрещенную.
•Для обнаружения двукратных ошибок наименьшее кодовое
расстояние должно быть dmin=3. В качестве примера разрешенных комбинаций в этом случае можно выбрать А3=010 и А6=101.
•Пусть теперь необходимо построить код, обеспечивающий исправление однократных ошибок. Выберем в качестве первой
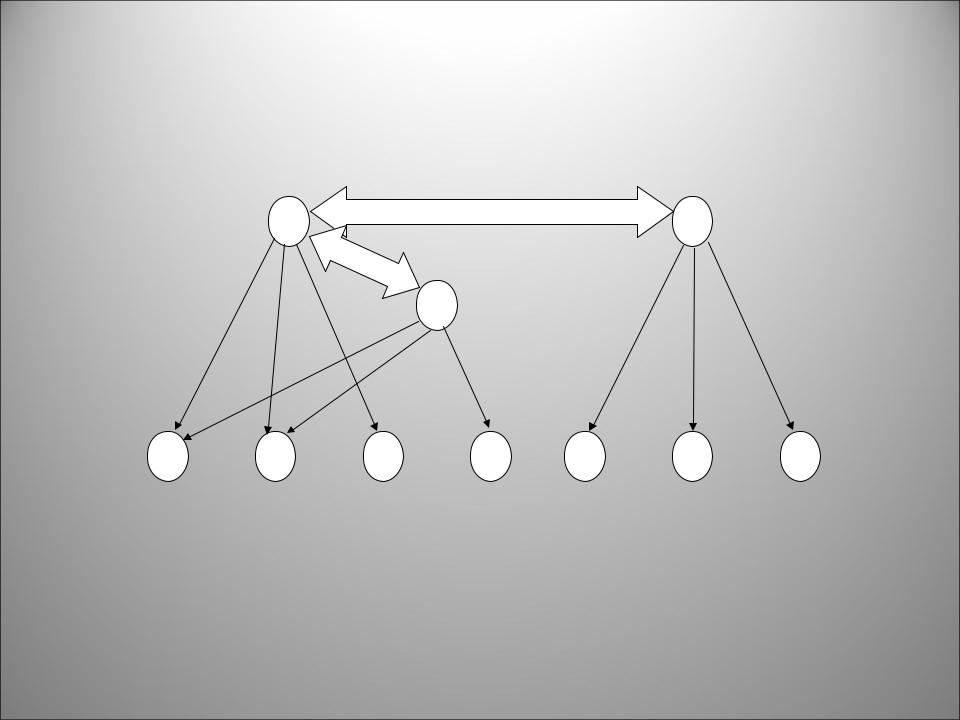
разрешенной комбинации А2=001. При однократной ошибке комбинация А2 перейдет в одну из трех комбинаций: А1=000, А4=011 или А6=101 (рис. 5.4). Эти комбинации объявляются запрещенными комбинациями для А2. Это означает, что при появлении одной из этих комбинаций на выходе канала связи будет принято решение, что передана комбинация А2.
А2 d=3 А7
d=2 А3
А1 |
А4 |
А6 |
А7 |
А3 |
А5 |
А8 |
Варианты перехода между кодовыми комбинациями при однократной ошибке.
•Допустим, в качестве второй разрешенной комбинации выбрана А3=010, отстоящая на расстоянии d=2. Ей соответствует подмножество запрещенных комбинаций А4=011, А1=000 и А7=110. Однако получилось пересечение подмножеств запрещенных комбинаций. При приеме запрещенных комбинаций А4 и А1 нельзя однозначно установить, какая комбинация была послана – А2 или А3. Если же в качестве второй разрешенной комбинации принять А7=110, которой соответствуют запрещенные комбинации А8=111, А5=100 и А3=010, то в этом случае подмножества запрещенных комбинаций не пересекаются и имеется однозначное соответствие принятой и переданной комбинации.
•Следовательно, при dmin=3 обеспечивается исправление всех однократных ошибок.
•В общем случае, для исправления ошибок кратности t минимальное
кодовое расстояние должно удовлетворять условию
• dmin ≥ 2t + 1 (5.3)
•Сможет ли командир исправить двукратную ошибку?
•Ответ: да, потому что 5 ≥ 2∙2+1
•Аналогично рассуждая, можно установить, что для исправления всех
ошибок кратности не более ошибок кратности не более удовлетворять условию
t и одновременного обнаружения всех τ (при τ ≥ t) кодовое расстояние должно
•dmin ≥ t + τ + 1