
- •Теория информационных процессов и систем
- •Лекции читает канд.техн.наук, доцент Литвинов Владислав Леонидович
- •Циклические коды
- ••Наибольшая степень х в слагаемом с ненулевым коэффициентом называется степенью полинома. Таким образом,
- ••Следовательно, если в качестве исходного взять некоторый полином g(x), то процесс получения разрешенных
- ••Основные свойства циклических кодов:
- ••Кодирование с использованием циклических кодов
- ••Второй:
- ••Кодирование циклических кодов с помощью сдвиговых схем
- ••Вычисление синдрома и исправление ошибок в циклических кодах
- ••Покажем, что синдромный многочлен,S(x) однозначно связан с многочленом ошибки e(x), а значит, с
- •Получение порождающих полиномов для циклических кодов
- ••Дальше остатки повторяются. Получили следующие остатки: 011, 110, 111, 101, 001, 010, 100.
- ••Дальше остатки повторяются. Получили следующие остатки: 111, 001, 010, 100. Всего 4 штуки.
- ••Пример. Выбрать порождающий полином циклического кода, исправляющего однократные ошибки и позволяющего передать 2000
- •Таблица неприводимых полиномов
- ••ГОСТ 28082-89 «Методы обнаружения ошибок при последовательной передаче данных» устанавливает в качестве основного
- •Непрерывные коды
- ••При этом кодирование кадра информационных символов в кадр кодового слова производится с учетом
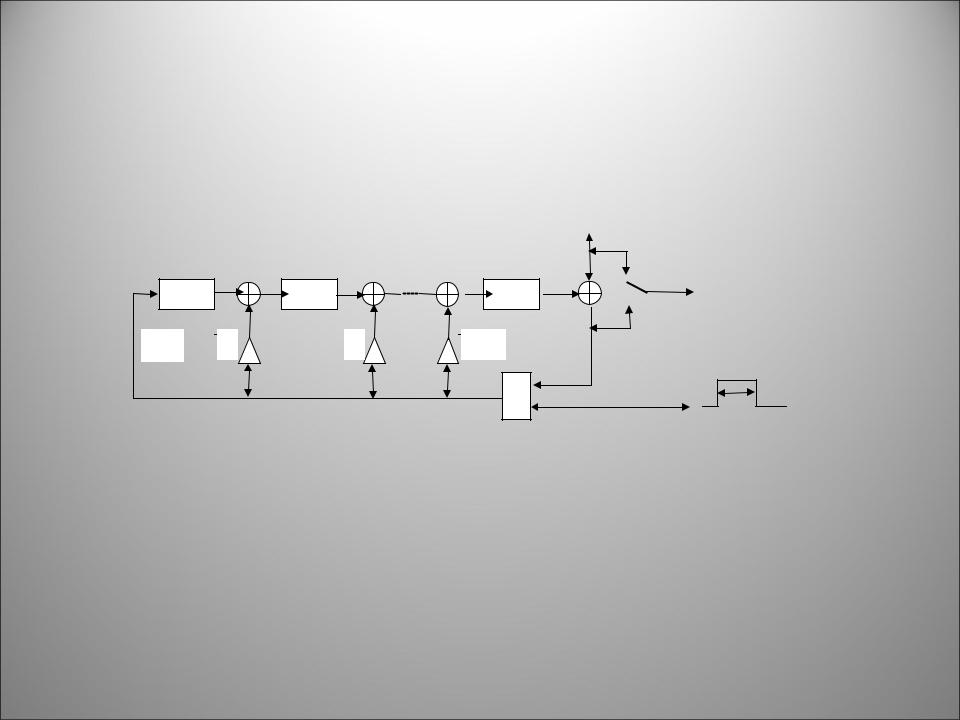
- ••Сверточный (цепной) алгоритм непрерывного кодирования
- ••Таким образом, каждый символ входной последовательности ak участвует в формировании двух проверочных символов:
- ••На приеме информационные и проверочные символы разделяются и регистрируются независимо друг от друга.
- ••Непрерывное кодирование с помощью импульсной переходной характеристики
•Кодирование циклических кодов с помощью сдвиговых схем
•Алгоритм кодирования, основанный на делении полиномов, можно реализовать, используя схему деления. Она представляет собой регистр сдвига, в котором цепи обратной связи замкнуты в соответствии c коэффициентами порождающего полинома g(x)
|
0 |
|
U |
|
1 |
n-k-1 |
|
g0=1 |
g1 |
g2 |
gn-k-1 |
& |
n-k |
|
|
|
k |
•Кодирование в схеме выполняется следующим образом:
•- k символов информационной последовательности m через переключатель, находящийся в верхнем (правом) положении, один за другим передаются в канал (выходной регистр) и одновременно с этим записываются в регистр проверочных
символов, в котором благодаря наличию цепей обратной связи g0 ... gn-k-1 формируется остаток от деления xn-k × m(x) на g(x) — проверочные символы;
•- начиная с (k+1)-го такта переключатель переводится в нижнее (левое) положение, и из сдвигового регистра выводятся (n-k) проверочных символов; цепь обратной связи при этом разомкнута.

•Для циклического (7,4)-кода, используемого в качестве примера и имеющего порождающий полином g(x) = x3+ x +1, схема кодирования выглядит следующим образом:
 mT
mT
r0 

 r1
r1  r2
r2
g0=1 |
g1=1 |
g2=0 |
|
|
|
g3=1 |
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разрешение |
||
|
|
|
|
||||
UT
n-k |
k |
•В этой схеме, в отличие от обобщенной схемы кодера, отсутствуют элементы в цепях,
где значения коэффициентов обратной связи gi равны нулю, там же, где коэффициенты передачи gi равны единице, цепь просто замкнута.
•На примере этого же кода и соответствующего ему кодера рассмотрим в динамике процесс кодирования произвольной последовательности m.
•Пусть m = (1001). Выходной код будет следующий: (1001110).

•Вычисление синдрома и исправление ошибок в циклических кодах
•Вычисление синдрома для циклических кодов является довольно
простой процедурой.
•Пусть U(x) и Û(х) полиномы, соответствующие переданному кодовому слову и принятой последовательности.
•Разделив Û(х) на g(x), получим
•Û(х) = q(x)× g(x) s(x),
•где - q(x) — частное от деления, s(x) — остаток от деления.
•Если Û(х) является кодовым полиномом, то он делится на g(x) без остатка, то есть s(x) = 0.
•Следовательно, s(x) ≠ 0 является условием наличия ошибки в принятой
последовательности, то есть синдромом принятой последовательности.
•Синдром s(x) имеет в общем случае вид
•S(x) = Sn- k-1 × xn-k-1 + Sn- k-2 × xn-k-2 +... + S1 × x + S0 .
•Очевидно, что схема вычисления синдрома является схемой деления, подобной схемам кодирования.

Û
S
r0 

 r1
r1  r2
r2
g0=1 |
g1=1 |
g2=0 |
g3=1 |
|
|
|
|
& |
n-k |
|
|
|
|
|
|
|
|
разрешение |
k |
•При наличии в принятой последовательности Û хотя бы одной ошибки вектор синдрома S будет иметь, по крайней мере, один ненулевой элемент, при этом факт наличия ошибки легко обнаружить, объединив по ИЛИ выходы всех ячеек регистра синдрома.

•Покажем, что синдромный многочлен,S(x) однозначно связан с многочленом ошибки e(x), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.
•Пусть e(x) — полином вектора ошибки.
•Тогда полином принятой последовательности
•Û (x) = U(x) e(x).
•Учтем, что
• Û (x) = q(x)× g(x) S(x), U(x) = m(x)× g(x),
•Тогда
•e, x Û x U x m x q x g x S x f x g x S x
•то есть
•синдромный полином S(x) есть остаток от деления полинома ошибки e(x) на порождающий полином g(x).
•Отсюда следует, что по синдрому S(x) можно однозначно определить вектор ошибки e(x), а следовательно, исправить эту ошибку.

Получение порождающих полиномов для циклических кодов
•Синдромный полином есть остаток от деления полинома ошибки e(x) на порождающий полином g(x). Для исправления ошибок необходимо выбрать такой порождающий полином, у которого количество различных остатков не меньше числа возможных ошибок. Только в этом случае все ошибки можно локализовать. Очевидно, что корректирующая способность кода будет тем выше, чем больше различных остатков может быть образовано при делении кодового полинома на порождающий полином.
•Наибольшее количество остатков обеспечивают т.н. неприводимые (синоним – примитивные) полиномы.
•Неприводимый полином в алгебре полей Галуа – это аналог простых чисел.
•Неприводимым называется полином, который делится без остатка только на 1 и сам на себя.

•Примером могут служить многочлены: x+1, x2+x+1, x3+x+1 и другие. Если неприводимый многочлен имеет степень p, то он дает 2p-1 остатков. Приводимые полиномы той же степени дают меньшее количество разных остатков. В этом можно убедиться. Разделим вектор ошибки 100000000… на неприводимый полином x3+x+1, которому соответствует комбинация 1011.
•10000000000 |1011
• 1011 |
1011100… |
Остатки: |
•0110 011
•0000
•1100110
•1011
• |
1110 |
111 |
•1011
• |
1010 |
101 |
•1011
• |
0010 |
001 |
•0000
• |
0100 |
010 |
•0000
• |
1000 |
100 |
• |
|
|

•Дальше остатки повторяются. Получили следующие остатки: 011, 110, 111, 101, 001, 010, 100. Всего 7 штук. Полином степени 3 должен давать 23-1=7 остатков.
•Теперь для сравнения разделим вектор ошибки на приводимый полином x3+x2+x+1, которому соответствует комбинация 1111.
•10000000000 |1111
• 1111 |
1100… |
•1110
•1111
•0010
•0000
•0100
•0000
•1000

•Дальше остатки повторяются. Получили следующие остатки: 111, 001, 010, 100. Всего 4 штуки.
•Иногда при выборе подходящего неприводимого полинома бывает полезно следующее свойство двучлена xn+1.
•Если n = 2p-1, то двучлен xn+1 можно разложить на неприводимые полиномы степени не больше p.
•Например
•x15+1= x24 1 +1=(x+1)(x2+x+1)(x4+x3+1)(x4+x+1)(x4+x3+x2+x+1).
•Можно сформулировать следующие правила составления порождающих полиномов:
1.порождающий полином должен быть неприводимым;
2.порождающий полином должен быть делителем двучлена xn+1;
3.степень полинома p должна быть настолько большой, чтобы количество остатков (2p-1) было не меньше количества ошибок, которые требуется локализовать;
4.число ненулевых членов полинома должно быть не меньше минимального кодового расстояния.

•Пример. Выбрать порождающий полином циклического кода, исправляющего однократные ошибки и позволяющего передать 2000 различных сообщений.
•Определим необходимое количество информационных разрядов. k≥log 2000. k=11.
•По правилу Хемминга (r ≥ log (n+1), для t=1) определим, что для исправления однократных ошибок требуется 4 проверочных разряда, следовательно, надо строить (15,11)-код.
•В (15,11)-коде возможно возникновение 15 одиночных ошибок, следовательно, нужен порождающий полином 4-й степени, так как при этом полиноме получаются 24-1=15 различных остатков от деления.
•Из разложения двучлена x15+1, приведенного выше, выбираем порождающий полином g(x)=(x4+x+1), так как он проще других, обеспечивающих ту же корректирующую способность кода.
