
Методы отделения (локализации) корней
Графический метод
Он
основан на построении графика функции
y=f(x).
Тогда искомым отрезком [а;в], содержащим
корень уравнения (1), будет отрезок оси
абсцисс, содержащий точку пересечения
графика с этой осью. Иногда выгоднее
представить исходную функцию в виде
разности двух более простых функций
f(x)=g(x)-g1(x)
и строить два графика
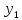 =g(x)
и
=g(x)
и
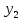 =g1(x),
точка пересечения которых и является
корнем уравнения (1), а отрезок на оси
абсцисс с корнем внутри и будет являться
интервалом изоляции. Этот метод хорошо
работает в случае, если исходное уравнение
не имеет близких корней и дает тем точнее
результат, чем мельче берется сетка по
оси ОХ.
=g1(x),
точка пересечения которых и является
корнем уравнения (1), а отрезок на оси
абсцисс с корнем внутри и будет являться
интервалом изоляции. Этот метод хорошо
работает в случае, если исходное уравнение
не имеет близких корней и дает тем точнее
результат, чем мельче берется сетка по
оси ОХ.
Пакет
Excel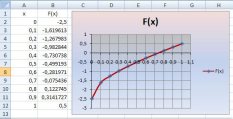
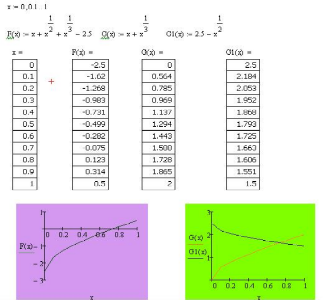
Первый
способ f(x)
= x+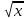 +
+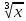 -2.5
-2.5
Второй
способ g(x)
= x+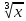 ;g1(x)
= 2.5 -
;g1(x)
= 2.5 -
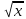
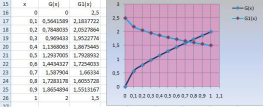
Искомый корень уравнения находится на отрезке [0,7;0,8]
Пакет MathCAD
Аналитический метод
Аналитический метод основан на следующем положении: если непрерывная и дифференцируемая на отрезке [a;b] функция f(x) принимает значения разных знаков на его концах (т.е. f(a)∙f(b)<0), то внутри данного отрезка содержится, по крайней мере, один корень уравнения (1), а если к тому же на [a;b] f'(x) сохраняет знак (функция f(x) – монотонная), то этот корень единственный.
Если исходное уравнение имеет близкие корни или функция f(x) сложная, то для выделения отрезков изоляции область изменения аргумента разбивают на отрезки длиной h (шаг) и последовательно проходят их, проверяя значение функции на их концах и выбирая нужные.
Для
функции F(x)
= x+ +
+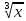 -2.5
производная имеет видF'(x)=1+
-2.5
производная имеет видF'(x)=1+
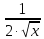 +
+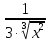 Областью допустимых значений аргумента
для производной является интервал (0;
+∞). При таких значениях аргумента
функцияF'(x)
всегда положительна, следовательно,
уравнение имеет единственный корень.
Областью допустимых значений аргумента
для производной является интервал (0;
+∞). При таких значениях аргумента
функцияF'(x)
всегда положительна, следовательно,
уравнение имеет единственный корень.
Блок-схема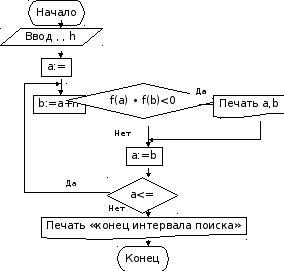
Pascal
Методы уточнения корней
Методы отделения корней весьма удобны и просты. Однако они дают ответ только на вопрос локализации корня и позволяют найти его грубое приближенное значение. Если же требуется найти более точное значение корня, то используют различные методы уточнения.
Метод половинного деления
Входная информация: отрезок [a;b] с корнем непрерывной функции f(x) внутри и точность определения корня ε.
Исходный
отрезок делится пополам точкой
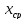 =
=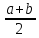 и
еслиf(
и
еслиf( )=0,
тоx
– корень уравнения. Если f(
)=0,
тоx
– корень уравнения. Если f(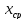 )≠0,
то из двух получившихся отрезков [a;
)≠0,
то из двух получившихся отрезков [a;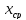 ]
и [
]
и [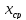 ;b]
выбирается тот, на концах которого
функция имеет противоположные знаки.
(Например, если f(a)
∙ f(
;b]
выбирается тот, на концах которого
функция имеет противоположные знаки.
(Например, если f(a)
∙ f(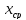 )<0,
то выбирается [a;
)<0,
то выбирается [a;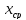 ];
если нет, то [
];
если нет, то [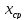 ;b]).
Продолжаем процедуру деления до тех
пор, пока |a-b|<
ε. Тогда последнее значение
;b]).
Продолжаем процедуру деления до тех
пор, пока |a-b|<
ε. Тогда последнее значение
 будет искомым корнем с точностью ε. Этот
метод всегда сходится к корню, но
требуется большое количество приближенийn,
которое можно определить из соотношения
ε ∙
будет искомым корнем с точностью ε. Этот
метод всегда сходится к корню, но
требуется большое количество приближенийn,
которое можно определить из соотношения
ε ∙
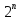 =
|b-a|
(так при |b-a|=1
и ε=0.001, n=10).
=
|b-a|
(так при |b-a|=1
и ε=0.001, n=10).
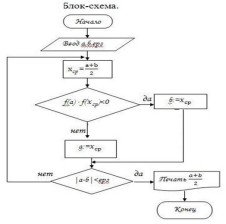
Pascal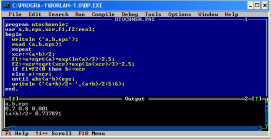
Пакет
Excel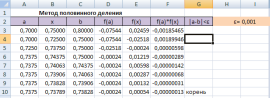
Пакет
MathCAD
Метод последовательных приближений
Исходное
уравнение F(x)
= x+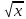 +
+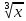 -2.5
преобразуем к видуx
= φ(x).
Если на рассматриваемом интервале
изоляции корня [0.7; 0,8] |φ’(x)|<1,
то расчетная формула примет вид :
-2.5
преобразуем к видуx
= φ(x).
Если на рассматриваемом интервале
изоляции корня [0.7; 0,8] |φ’(x)|<1,
то расчетная формула примет вид :
 =φ(
=φ( ),
и при этом итерационный процесс
приближения к корню будет сходящимся.
),
и при этом итерационный процесс
приближения к корню будет сходящимся.
В нашем случае непосредственный выбор расчетной формулы вызывает затруднения. Поэтому воспользуемся следующим приемом.
Введем
в рассмотрение произвольный параметр
λ>0 . Тогда функцию φ(x)
можно представить как φ(x)
= x
- λ∙F(x).
Затем, варьируя параметр λ, добиваемся
условия сходимости: |φ’(x)|<1
на [a;
b].
φ’(x)=1-λ∙F’(x).
Для выполнения сходимости λ=
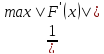 на [a;
b].
на [a;
b].
Для рассматриваемого примера:
max|F’(x)|
на (a;
b)
= max|
(1 +
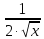 +
+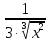 )|= 2 (приx=0.7).
λ
=
)|= 2 (приx=0.7).
λ
=
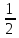 .
.
Расчетная формула метода итерации примет вид:
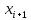 =
=
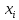 -
-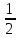 ∙(
∙(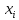 +
+ +
+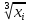 -2.5)
=
-2.5)
=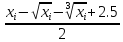 .
.
Блок-схема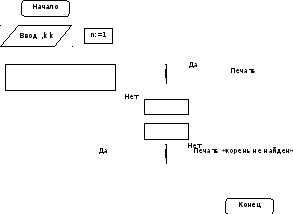
Pascal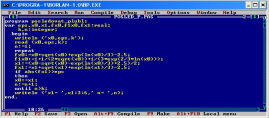

Пакет
Excel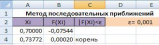

Пакет MathCAD
Метод Ньютона
Этот
метод можно рассматривать как частный
случай метода простой итерации с
рекуррентной формулой 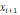
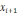 =
=
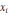 –
–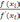
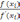 и тем же принципом выбора начального
приближения
и тем же принципом выбора начального
приближения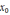
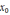 .
.
Последовательность
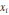
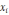 является сходящейся, ибо
является сходящейся, ибо
 (x)
=
(x)
=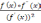
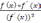 и
и
 (x)=0.
Что означает, что если
(x)=0.
Что означает, что если
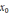 выбрано из малой окрестности корня, то
выбрано из малой окрестности корня, то
 (x)≤1.
При произвольном
(x)≤1.
При произвольном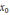
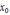 итерации будут сходиться, если всюду
итерации будут сходиться, если всюду
|f
(x) * 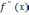
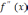 |
<
|
<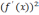
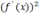 .
.
Геометрически
метод Ньютона соответствуют
последовательному проведению касательных
к кривой y = f(x) в точках (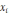
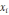 ;
f (
;
f (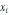
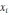 ))
и выборе в качестве нового приближения
))
и выборе в качестве нового приближения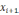
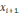 точки пересечения их с осью абсцисс.
точки пересечения их с осью абсцисс.
Для
рассматриваемого нами примера (F(x)
= x+
 +
+
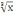 -2.5)
первая производная равнаF‘(x)=1+
-2.5)
первая производная равнаF‘(x)=1+
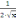
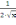 +
+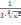
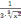 ,
а вторая производная имеет вид
,
а вторая производная имеет вид
F’’(x)
= - 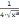
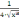 -
-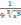
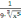 . Итерационная формула примет вид:
. Итерационная формула примет вид:

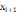 =
=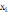
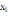 -
-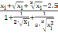
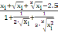 .
.
В
качестве начального приближения
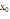
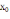 берется
тот конец интервала изоляции, на котором
функция и ее вторая производная имеют
одинаковые знаки. Найдем значения
функции на концах отрезка [0,7; 0,8]:
берется
тот конец интервала изоляции, на котором
функция и ее вторая производная имеют
одинаковые знаки. Найдем значения
функции на концах отрезка [0,7; 0,8]:
F(0,7)=0.7+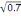
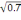 +
+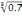
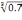 -2.5≈
-0,075<0;
-2.5≈
-0,075<0;
F’’(0.7)=
- 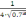
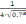 -
-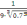
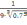 ≈-0,6282<0.
≈-0,6282<0.
Таким
образом, за начальное приближение примем
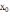
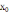 =0.7.
=0.7.
Процесс
итераций идет до тех пор, пока |F(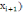
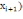 |<ε.
В случае неудачного выбора рекуррентной
формулы получается расходящийся процесс,
и условие сравнения с точностью не
достигается. Для исключения подобной
ситуации введем счетчик итерацииn,
увеличивающийся каждый раз на единицу,
и поставим искусственное условие
продолжения итерации в случае n<=k.
В противном случае завершим алгоритм
с выводом текстового сообщения о
невозможности получения корня за
заданное количество k
шагов.
|<ε.
В случае неудачного выбора рекуррентной
формулы получается расходящийся процесс,
и условие сравнения с точностью не
достигается. Для исключения подобной
ситуации введем счетчик итерацииn,
увеличивающийся каждый раз на единицу,
и поставим искусственное условие
продолжения итерации в случае n<=k.
В противном случае завершим алгоритм
с выводом текстового сообщения о
невозможности получения корня за
заданное количество k
шагов.
Блок-схема

Pascal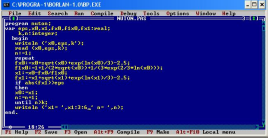

Пакет
Excel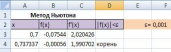
Пакет
MathCAD
