
Физика
.docx18. Смещение молекул в движущих слоях жидкости сопровождается действием сил сопротивления (Внутреннее трение). Оно характеризуется вязкостью . Вязкость обусловлена межмолекулярным воздействием и зависит от природы жидкости и температуры. В жидких телах смещение молекул под действием внешних сил относительно друг друга происходит легко, поэтому упругих сил при сдвиге не возникает – текучесть. Ньютон установил, что сила внутреннего трения тем больше, чем больше площадь соприкосновения слоев и зависит от изменения скорости течения жидкости при переходе от слоя к слою.
Fтр=n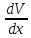 S
S
- коэффициент внутреннего трения, вязкость.
dV/dX – градиент скорости – изменение скорости, отнесенное к расстоянию между слоями в направлении, перпендикулярном скорости.
S – площадь соприкосновения слоев.
Ньютоновские жидкости – если вязкость в силе трения зависит только от природы жидкости и температуры (вода, НМС, плазма крови, лимфа, бензол, Этиловый спирт).
Неньютоновские жидкости – если вязкость в силе трения зависит и от природы, температуры и от режима течения жидкости (эмульсии, суспензии, ВМС, кровь, протоплазма). const.
Пуазейль установил, что средняя скорость (υср) ламинарного течения жидкости по круглой трубе постоянного сечения прямо пропорционально градиету давления:
P1- P2
l , квадрату радиуса трубы (r 2) и обратно пропорционально вязкости жидкости ( η );
υср.= P1 – P 2 r 2 , где
l 8η
P1 и P 2 – давления в начале и конце трубы , длиной l . υ сред. Течения жидкости определяет кол-во жидкости, протекающей через поперечное сечение S в ед-цу времени:
Q = υср. S, S = πr2
Формула Пуазейля
Q= P1 – P 2 π r 4 или Q= P1 – P 2 , где
l 8η ω
ω=8lη/πr4 – гидравлическое сопротивление возрастает с уменьшением радиуса трубы.
Падение давления Δ P= P1-P2 вдоль отдельной трубы, определяемое формулой Пуазейля; затем в виде P1-P2 =Qω, ω- гидравлическ.сопрот-е., т.е. при фиксированном объеме Q протекающей жидкости ΔP зависит от ω. В кровеносной системе падение давления вдоль кроветока зависит от гидравлического сопротивления разветвления, которое нах –ся по формулам для послед – го и парал.-го соед.-ний;
ω = ω1+ ω2+… +ωn – посл.соед.-е.
ω= ( 1 +1 +…1 ) –1 - парал. соед.-е.
ω1 ω2 ωn
Здесь проведена аналогия с законом Ома: 1) гидравлическое сопротивление ω =электрич. сопротив-е. R. 2) разность давлений ΔР= разность потенциалов. 3) Q = сила тока J.
З.Ома: J(ампер или кулон/с) = ΔU /R ф.Пуазейля: Q(м3/с)=ΔP/ω
20. Турбулентное течение – вихревое. Возникает при увеличении v течения вязкой жидкости вследствие неоднородности давления по поперечн. сечению трубы. При турб. течении υ частиц в каждом месте беспрерывно и хаотически меняется.
Число Рейнольдса крит. =2300.
-
При Re < Re крит. (2300) => течение ламинарное.
-
При Re > Re крит. => турбулентное течение.
Re = d /η Re = d /ν , где
-
- плотность жидкости
-
– скорость течения
-
d – диаметр трубы
-
- вязкость жидкости. Измеряется в СИ – ( М2\с), в СГС ( стокс).
υ крит.= Re *(ν/ r)
- ν - кинематическая вязк. жидкости , r – радиус сосуда, Re - зависит от природы: Н2О – 2300; кровь – 1000.
Течение крови в артериях в норме является ламинарным, небольшая турбулентность возникает вблизи клапанов. При патологии, когда вязкость крови меньше нормы, Re > Re крит. 1000 => движение турбулентное.
Турбулентное течение связано с дополнительной работой сердца шум, возникающий при турбулентном течении крови диагностика заболеваний.
Причины перехода ламинарного течения крови в турбулентное:
-
отложение холестерина на стенках сосуда (шум на дуге аорты)
-
врожденное отверстие в межжелудочковой перегородке (шумы в плеч.аорте).
-
множественные раветвления.
19. Закон Бернулли: в различных точках линии тока идеальной жидкости сумма статического, динамического и гидростатического давлений одинакова:
Формула: P+ρυ2/2+ρgh=const
-
Статическое давление –P возникает от работы сердца, не связано с движением жидкости.
-
Динамическое (скоростное) давление ρυ2/2 связано с кинетической энергией потока жидкости, проявляется при торможении жидкости.
Формула P+ρυ2/2=Pn ( полное давление)
- Гидростатическое давление - ρgh связано с потенциальной энергией и перепадом высот.
Статическое и гидростатическое давление по своему действию одинаковы, но гидростатическое давление распред. объема жидкости (130 мм.рт.ст. = Ргол. – Рниж.кон. при росте =180 см. стоя). В невесомости это давление отсутствует.
16. Понятие функциональной зависимости
Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.
Например,
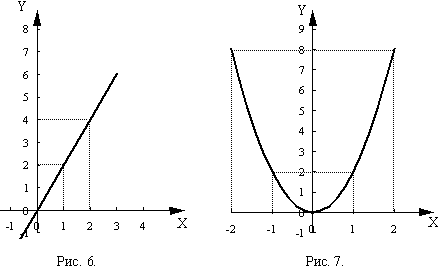
в функции у = 2 * х каждому значению х соответствует
в два раза большее значение у .
В функции ![]() каждому
значению усоответствует
2 определенных значения х .
Графически это выглядит так (рис. 6, 7
соответственно):
каждому
значению усоответствует
2 определенных значения х .
Графически это выглядит так (рис. 6, 7
соответственно):
 Понятие
корреляционной зависимости и ее
направленности
Понятие
корреляционной зависимости и ее
направленности
Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
17. Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимыхи независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
Цели регрессионного анализа
-
Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
-
Предсказание значения зависимой переменной с помощью независимой(-ых)
-
Определение вклада отдельных независимых переменных в вариацию зависимой
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
[править]Математическое определение регрессии
Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X1,X2,...,Xp — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1 = x1,X2 = x2,...,Xp = xp определено условное математическое ожидание
y(x1,x2,...,xp) = E(Y | X1 = x1,X2 = x2,...,Xp = xp) (уравнение линейной регрессии в общем виде),
то функция y(x1,x2,...,xp) называется регрессией величины Y по величинам X1,X2,...,Xp, а её график — линией регрессии Y по X1,X2,...,Xp, или уравнением регрессии.
Зависимость Y от X1,X2,...,Xp проявляется в изменении средних значений Y при изменении X1,X2,...,Xp. Хотя при каждом фиксированном наборе значений X1 = x1,X2 = x2,...,Xp = xpвеличина Y остаётся случайной величиной с определённым рассеянием.
Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении X1,X2,...,Xp, используется средняя величина дисперсии Y при разных наборах значений X1,X2,...,Xp (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).
[править]Метод наименьших квадратов (расчёт коэффициентов)
На
практике линия регрессии чаще всего
ищется в виде линейной
функции Y = b0 + b1X1 + b2X2 +
... + bNXN (линейная
регрессия), наилучшим образом приближающей
искомую кривую. Делается это с
помощью метода
наименьших квадратов,
когда минимизируется сумма квадратов
отклонений реально наблюдаемых Y от их
оценок ![]() (имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):
(имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):
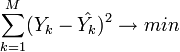
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y(x1,x2,...xN).
Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:
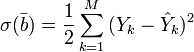
Условие минимума функции невязки:
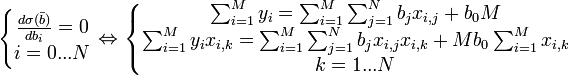
Полученная система является системой N + 1 линейных уравнений с N + 1 неизвестными b0...bN
Если представить свободные члены левой части уравнений матрицей
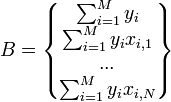
а коэффициенты при неизвестных в правой части матрицей

то
получаем матричное уравнение: ![]() ,
которое легко решается методом
Гаусса.
Полученная матрица будет матрицей,
содержащей коэффициенты уравнения
линии регрессии:
,
которое легко решается методом
Гаусса.
Полученная матрица будет матрицей,
содержащей коэффициенты уравнения
линии регрессии:
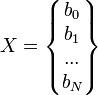
Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.
[править]Интерпретация параметров регрессии
Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.
Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X1X2, X1X2X3, свидетельствующее о наличии взаимодействий между признаками X1, X2 и т. д.
