01_02_Сл_соб_Часть_1_2005

Случайные события

17

Пример:

Из урны, содержащей 4 белых и 3 черных шара, вынимают 2 шара. Найти вероятность того, что оба шара будут белыми.

Событие С={ оба шара белые}; представим С как произведение 2-х событий С = A B , где А={первый шар белый}, В={второй шар белый}.

P (AB)= P (A) P (B A); Р(А) = 74 .

Предположим , что событие А произошло, т.е. в урне осталось 6 шаров, 3 из

них белые, тогда P (B		A)=	3	=	1		P (C )=	4		1	=	2
			6		2 .			7		2		7 .

ОСобытие А называется независимым от события В, если его вероятность не зависит от того, произошло событие В или нет, т.е. P (A B)= P (A). В

противоположном случае, если P (A B)≠ P (A), событие А зависит от В.

Пример:

В урне 5 белых и 2 черных шара. Из нее вынимают один за другим 2 шара. Найти вероятность того, что они будут разных цветов.

Решение: Событие С ={шары разных цветов} распадается на сумму 2-х несовместных событий: С1={белый, черный}, С2{черный, белый}; С=С1+С2. Вычислим вероятность события С1:

Р(С1) - вероятность того, что 1-й шар белый, умноженная на условную вероятность того, что второй черный, при условии, что первый белый:

P (C1 )= 75 62 = 215 .

Вычислим вероятность события С2: P (C2 )= 72 56 = 215 .

По правилу сложения вероятностейP (C )= P (C1 )+ P (C2 )= 1021 .

Для произвольного числа событий вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.

P (A1 A2 ... An )= P (A1 ) P (A2 A1 ) P (A3 A1 A2 ) ... P ( An A1 A2 ... An−1 )

Пример:

В ящике 6 белых, 8 красных и 4 синих шара. На удачу извлекают 1 шар без возвращения. Чему равна вероятность того, что на первом шаге появится белый, на 2-м – красный и на 3-м – синий шар?

Решение: Событие А ={на первом шаге появится белый шар}, событие В={на втором шаге появится красный шар}, событие С={на третьем шаге появится синий шар}.

P (A)=		6	=	1	; P (B		A)=		8	; P (C		AB)=		4	=	1	; P (ABC )=	1			8		1	= 0, 039 .
	18			3				17					16			4		3		17			4

18	Лекции 1-2

Пример:

Среди продаваемых телевизоров 95% стандартных, из них 86% высшего качества. Чему равна вероятность покупки телевизора высшего качества? Решение: А={телевизор стандартный} Р(А)=0,95; В={телевизор высшего качества, при условии, что он стандартный} Р(В/А)=0,86; Р(А·В)=Р(А) ·Р(В/А)=0,95·0,86=0,82.

Для независимых событий правило умножения вероятностей принимает простой вид: Р(А·В)=Р(А)·Р(В), т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Для нескольких независимых событий Р(А1·А2·…·Аn)=Р(А1)·Р(А2)·…·Р(Аn)

или P	n		n
	∏Ai		= ∏P (Ai ), т.е. вероятность произведения нескольких незави-
	i =1		i =1

симых событий равна произведению вероятностей этих событий.

2.3. Вероятность появления хотя бы одного события

Пусть в результате опыта могут появиться n независимых в совокупности событий А1,А2 ,…,Аn , вероятности которых Р(А1), Р(А2),…,Р(Аn) – известны.

А - событие, заключающееся в появлении хотя бы одного из событий

А1, А2,…, Аn, А=А1+А2 + …+Аn .

A - событие, заключающееся в том, что ни одно из событий A1, A2 ,..., An

не наступило: A = A1 A2 … An .

A + A = Ω, P(A + A)= P(Ω)=1, P(A)+ P(A)=1 P(A)=1− P(A),

P(A)=1− P(A1 A2 … An ), P(A)=1− P(A1 ) P(A2 ) … P(An ),

P(A1 )=1− P(A1 )= q1 ; P(A2 )=1− P(A2 )= q2 ; P(An )=1− P(An )= qn ;

P(A) =1−q1q2...qn .

Пример:

Вероятность поражения цели 1-м стрелком равна 0,9; 2-м - 0,8; 3-м - 0,6; 4-м - 0,7. Какова вероятность попадания при залпе?

Решение: Проще всего решить задачу через вероятность, противоположного события. Найдём q1, q2 , q3 , q4 – вероятности промахов 1, 2, 3, 4-го стрелка со-

ответственно.

q1=0,1; q2=0,2; q3=0,4; q4=0,3; P=1- q1q2q3q4 ; P=1-0,1·0,2·0,4·0,3=0,9976.

Случайные события

19

2.4. Формула полной вероятности

Следствием правил сложения и умножения вероятностей является формула полной вероятности.

Пусть проведен опыт, об условиях которого можно сделать n взаимоисключающих предположений (гипотез) H1 ,H2 ,...,Hn , образующих полную

группу:

H1 + H2 +...+ Hn = Ω, Hi H j = (i ≠ j).

Каждая гипотеза представляет собой некоторое событие. Вероятности реализации гипотез известны: Р(H1), Р(H2),…,Р(Hn).

Результат опыта – событие А, которое может появиться только вместе с одной из гипотез, условные вероятности события А при каждой из гипотез заданы: P(A/H1), P(A/H2),…,P(A/Hn). Найдем вероятность события А, для чего представим А как сумму n несовместных событий:

						n
		A = H1 A + H2 A +…+ Hn A = ∑Hi A.
						i
По правилу сложения вероятностей
P(A)		n		n				Hi ) .
	= P	∑Hi	A	= ∑P(Hi A), P(Hi A) = P(Hi ) P( A
		i		i
				n
Следовательно,				P (A)= ∑P (Hi ) P (A		Hi ).

i

Таким образом, вероятность события А в опыте с гипотетическими условиями равна сумме произведений вероятности каждой гипотезы на условную вероятность события при условии гипотезе.

Пример:

имеются три одинаковые на вид урны; в первой 2 белых шара и 3 черных, во второй – 4 белых и 1 черный, в третьей – 3 белых шара. Некто подходит наугад к одной из урн и вынимает из нее один шар. Найти вероятность того, что этот шар будет белым.

Решение: А={появление белого шара}.

Выдвигаем 3 гипотезы: Н1={выбрана первая урна}; Н2={выбрана вторая урна}; Н3={выбрана третья урна}.

P (H1 )= P (H2 )= P (H3 )= 1												;	Р(А/Н1) =	2	;	Р(А/Н2) =	4	; Р(А/Н3)=1;
											3			5			5
P (A)=	1		2	+	1		4	+	1	1 =	11 .
	3		5		3		5		3		15

Пример:

Партия деталей на 20% изготовлена на заводе №1, на 30% - на заводе №2, на 50% - на заводе №3. Вероятности выпуска нестандартных деталей:

Завод №1 – 0,01, завод №2 – 0,005, завод №3 – 0,006.

Какова вероятность, что взятая наугад деталь нестандартная? Решение:

20	Лекции 1-2

Гипотезы:Н1={деталь изготовлена на заводе №1}; Н2={деталь изготовлена на заводе №2}; Н3={деталь изготовлена на заводе №3 }

Р(Н1)=0,2; Р(Н2)=0,3; Р(Н3)=0,5; Р(А/Н1)=0,01; Р(А/Н2)=0,005; Р(А/Н3)=0,006; Р(А)=0,2·0,01+0,3·0,005+0,5·0,006=0,0065.

2.5. Формула Бейеса (теорема гипотез)

Формула Бейеса позволяет переоценить вероятности гипотез на основании результатов опыта. Пусть до опыта об его условиях сделан ряд предположений (гипотез) H1,H2,…,Hn, гипотезы образуют полную группу:

n

∑Hi = Ω, Hi H j = ,i ≠ j , и известны «априорные» (доопытные, от латин-

i=1

n

ского «a priori») вероятности: P(H1), P(H2 ),..., P(Hn ) , ∑P(Hi ) =1. В резуль-

i=1

тате проведения опыта произошло событие А. Найдем «апостериорные» (послеопытные, от латинского «a posteriori») вероятности гипотез: Р(Н1/А),

Р(Н2/А),…, Р(Нn/А).

Решение: т.к. событие А может появиться только вместе с одной из гипотез, то:

P(Hi A)= P(Hi )P(A Hi )= P(A)P(Hi A), P (Hi )P (A Hi )= P (A)P (Hi A).

Разделим на Р(А):

P(Hi

A) =

P(Hi )P( A

Hi )

.

По формуле полной вероятности

P( A)

n

P(A) = ∑P(Hi )P(A

Hi ) ,

i=1

P (Hi

A)=

P (Hi )P (A

Hi )

,

i =1,2...,n .

n

∑P (Hi )P (A

Hi )

i=1

Спомощью этой формулы возможен пересчет вероятностей гипотез после получения дополнительной информации, что опыт дал результат A.

Пример:

Среди людей 5% мужчин и 0,25% женщин дальтоники. Наугад избранное лицо из группы, состоящей из 100 мужчин и 100 женщин, оказалось дальтоником. Какова вероятность, что это мужчина?

Решение: Гипотезы: Н1={выбран мужчина}; Н2={выбрана женщина} Априорные вероятности гипотез:

Случайные события																										21
	P (H1 )= 100	=	1	; P (H2 )=						100 =		1 .
	200		2							200		2
	В результате опыта появилось событие А: А={выбранный человек - дальто-
	ник}.
	Условные вероятности события А при гипотезах Н1, Н2
					P (A				H1 )= 0, 05, P (A									H2 )= 0, 0025 .
	Апостериорная вероятность гипотезы
				P(H1			A) =					P(H1 ) P( A								H1 )						=
											P(H1 )P( A				H1 ) + P(H2 )P( A								H	2 )
						1
				=			2 0,05					0,05									500			20
													=								= 525 =			21 .
					1					1						0,0525
					2	0,05 + 2 0,0025

Пример:

имеются три урны; в первой 1 черный и 3 белых шара, во второй – 2 белых и 3 черных, в третьей – 3 белых шара. Некто подходит наугад к одной из урн и вынимает из нее один шар. Этот шар оказался белым. Найти апостериорные («послеопытные») вероятности того, что шар вынут из 1-й, 2-й, 3-й урны.

Решение: Н1={выбрана 1-я урна}; Н2={выбрана 2-я урна}; Н3={выбрана 3-я

урна}. Априорные вероятности гипотез: Р(H1) = Р(H2) = Р(H3) = 13 .

В результате опыта появляется событие А={вынут белый шар}. Условные вероятности события А при гипотезах Н1, Н2, Н3

P (A		H1 )=				3			;	P (A				H2 )				=	2			; P (A					H3 )=1.
						4													5
Апостериорные вероятности гипотез:
											1				3
P (H1					A)=						3				4							=	15		;
						1				3	+	1				2	+	1	1				43
						3				4		3				5		3
												1				2							8
P (H2					A)=							3			5							=			;
						1				3	+	1				2	+	1	1				43
						3				4		3				5		3
												1		1									20 .
P (H3					A)=							3										=
						1				3		1				2		1
											+						+		1				43
						3				4		3				5		3

Таким образом, после свершения опыта и появления события А вероятности гипотез изменились. Самой вероятной оказалась гипотеза H3, наименее вероятной гипотеза H2.

22	Лекции 1-2

2.6. Повторение опытов. Формула Бернулли

Рассмотрим сложный опыт, состоящий из нескольких более простых. В каждом из них может появиться или не появиться событие А.

Пример:

Пример:

Пример:

Произведена серия из n выстрелов. Событие А – поражение цели. Опыты называются независимыми, если вероятность события А в каждом опыте не зависит от результатов других опытов.

Найдем вероятность появления события А m раз в серии из n опытов. Обозначим соответствующую вероятность Pn(m). Вероятность появления события А при единичном испытании равна p, вероятность наступления проти-

воположного события A при единичном испытании q = 1 - p. Исход серии испытаний, состоящий в том, что событие А наступило m раз и не наступило n - m раз, может реализоваться несколькими способами. Вероятность каждо-

го такого исхода серии равна pmq(n−m) .

Поскольку порядок, в котором в серии появляются события А и A не существенен, число различных способов реализации m успехов в серии из n опы-

	тов есть число сочетаний из n по m: Cnm =	n !	.
		m !( n − m )!

Произведено 4 выстрела, из них 2 в цель. Решение:

Обозначим попадание ↑, промах 0.

Исходы: 0↑↑0, ↑00↑, ↑↑00, 00↑↑, ↑0↑0, 0↑0↑, C42 = 24! 2! ! = 22324 = 6 .

Таким образом, вероятность того, что в результате n опытов событие А произойдет m раз, равна:

P (m) =Cm pmq(n−m) =		n!		pm (1− p)n−m .
n	n	m!(n −m)!

Это соотношение носит название формулы Бернулли. С ее помощью можно выразить вероятности более сложных событий.

Вероятность того, что в n испытаниях событие А наступит

менее m раз:	Pn (0) +Pn (1) +...+Pn (m −1) ,
более m раз:	Pn (m +1) +Pn (m +2) +... +Pn (n) ,
не менее m раз:	Pn (m) +Pn (m +1) +... +Pn (n) ,
не более m раз:	Pn (0) +Pn (1) +... +Pn (m) .

В мастерской 4 мотора. Вероятность нормальной работы каждого 0,9. Чему равна вероятность нормальной работы в данный момент только: a) 4-х моторов; b )3-х моторов; с) 2-х моторов?

Решение:

a) P4 (4)= C44 p4q4−4 = 4!4!0! 0,94 0,10 = 0,6561,

Случайные события

23

b) P4 (3)= C43 p3q4−3 = 3!4!1! 0,93 0,11 = 0,2916 , c) P4 (2)= C42 p2q4−2 = 2!4!2! 0,92 0,12 = 0,0486 .

Пример:

Какова вероятность того, что при 10 бросаниях игральной кости два раза выпадут два очка?

Решение:

p = 16 , n=10, m=2, q = 1- p = 56 .

P	(2)= C2		1 2			5 10−2		=	10!		58	= 0,29 .
											10
10	10		6			6
									8! 2! 6

Пример:

На самолете установлены 4 турбины.

Вероятность исправности каждой из них – 0,99. Какова вероятность нормального полета, если он обеспечивается при 2-х работающих турбинах?

Решение: Р=Р4(2)+Р4(3)+Р4(4)=0,9963.

!Если рассмотреть разложение по степеням x функции (px +q)n ,то, по

формуле бинома Ньютона,

n

(px + q)n = ∑Cnm pmqn−m xm = qn +Cn1 pqn−1x +Cn2 p2qn−2 x2 +...+ pn xn ,

m=0

т.е., вероятности Pn(m) являются коэффициентами при xm в разложении бинома (px +q)n . В связи с этим совокупность вероятностей Pn(m) назы-

вают биномиальным законом распределения вероятностей (это понятие будет обсуждаться при рассмотрении случайных величин).

!Формула Бернулли допускает следующее обобщение. Пусть в результате единичного опыта возможны элементарные исходы A1, A2 ,…, Ak , обра-

зующие полную группу событий и происходящие с вероятностями p1, p2 ,…, pk , p1 + p2 +…+ pk =1. Вероятность того, что в серии из n не-

	зависимых испытаний событие A1				произойдет m1 раз, событие A2 – m2
	раз,…, событие Ak	– mk	раз, m1 + m2 +…+ mk = n , равна
	P (m ,m ,...m ) =				n!			p m1	p m2	...p mk .
				m !m !... m !
	n	1 2	k					1	2	k
				1	2	k

Совокупность величин Pn (m1,m2 ,...mk ) называют полиномиальным рас-

пределением.

24	Лекции 1-2

2.7. Предельные случаи формулы Бернулли

Если серия состоит из большого числа испытаний, пользоваться формулой Бернулли достаточно трудно, отношение факториалов сложно вычислить с достаточной точностью. Для упрощения вычислений используются формулы, полученные из формулы Бернулли в результате предельных переходов.

2.7.1. Локальная предельная теорема Муавра-Лапласа

ТЕсли вероятность p появления события А в каждом испытании отлична от нуля и единицы (0<p<1), то вероятность P n (m) того, что при n неза-

висимых испытаниях событие А появляется m раз при n →∞ удовлетворяет соотношению

Pn (m)

→1, где

x =

m −np

,

ϕ(x) =

1

е

−

x2

– функция Гаусса.

2

1

ϕ(x)

n→∞

npq

2π

npq

Таким образом, при больших n

P

(m)≈

1

ϕ(x).

n

npq

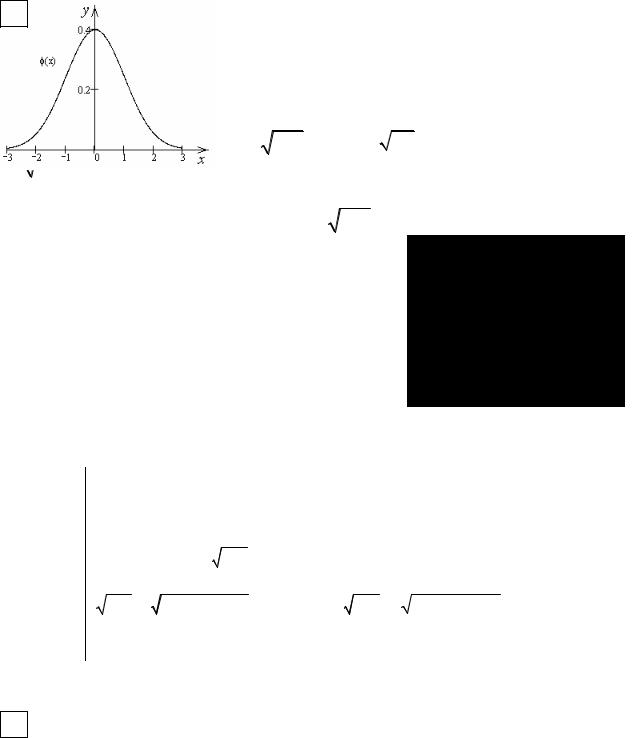
График функции Гаусса приведен на рисунке. Функция достаточно быстро убывает по мере удаления от начала координат –

ϕ (5)≈10−6 .

На практике локальную теорему Муавра-
Лапласа используют, если							p и q не малы,
а npq > 9			Так,		при		n = 40 , m = 20 ,
p = q = 0,5			погрешность приближения со-
ставляет 0,6%.
Пример:		Найти вероятность того, что при 10 выстрелах мишень будет поражена 8 раз,
		если вероятность попадания при одном выстреле p =0,75.
		Решение: P (8)≈					1		ϕ(x) , n =10, p = 0, 75, q =1−0, 75 = 0, 25, m = 8 ,
					10		npq
		1		=	1				= 0,730 ; x = m −np =	8 −10 0, 75	= 0,360;
			npq		10 0,75 0,25					10 0, 75 0, 25
									npq
		ϕ(0,360) = 0,374 ; P10 (8) = 0,730 0,374 = 0, 273 . Отметим, что даже в таких

условиях (npq<2) ошибка приближения около 3 %.

2.7.2. Интегральная предельная теорема Муавра - Лапласа

ТЕсли вероятность p события А в каждом испытании отлична от 0 и 1 (0<p<1), то при n → ∞ вероятность того, что событие А наступит в n ис-

Случайные события

25

пытаниях не менее m1

раз, но не более m2

раз, удовлетворяет соотношению:

1

x2

e−

z2

P

(m ,m )→

x∫

dz =Ф(x )−Ф(x ),

2

n

1 2

2π

2

1

1

= m2 −np

где

x = m1 −np , x

,

1

npq

2

npq

1

x

z2

а Ф(x)=

∫e−

dz – функция Лапласа.

2

2π

0

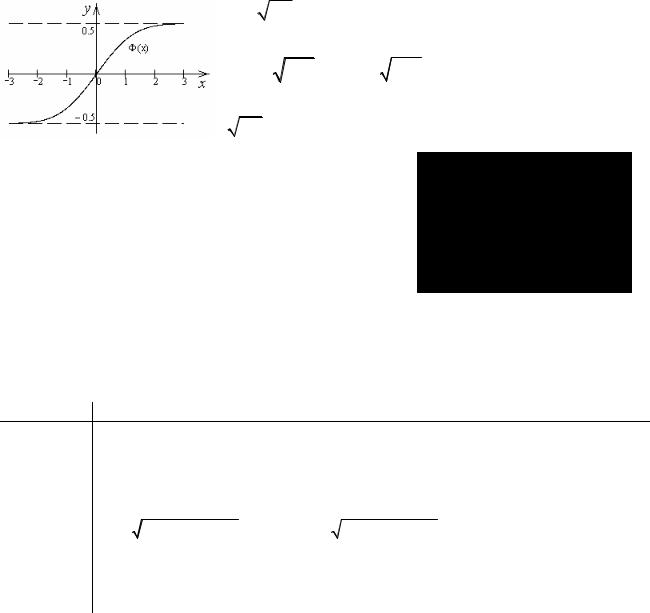
График функции Лапласа приведен на

рисунке. Функция достаточно быстро

приближается

к

своим

асимптотам

1

y = ±

2

по мере удаления от начала

координат – 12 −Ф(5)≈10−6 .

В приложении приведены таблицы значений функций Гаусса и Лапласа. Так как первая – четная, а вторая – нечетная, значения приведены только для неотрицательных значений аргумента.

Пример:

Вероятность поражения мишени при одном выстреле 0,75. Чему равна вероятность того, что при 100 выстрелах мишень будет поражена не менее 70 и не более 80 раз?

Решение:

x =	70 −100 0,75		= −1,15 ; x	=	80 −100 0,75		=1,15.
1	100	0,75 0,25	2		100	0,75 0,25

Ф(x1 ) =Ф(−1,15) = −Ф(1,15) = −0,3749 (функция Лапласа нечётна).

Ф(x2 ) =Ф(1,15) = 0,3749 .

P100 (70,80)≈Ф(1,15) −Ф(−1,15) = 2Ф(1,15) = 0,7498 .

2.7.3. Формула Пуассона

Если n велико, а p мало, мы имеем дело с редкими событиями, та же вероятность P n (m) вычисляется приближенно по формуле Пуассона:

P n (m)≈	λme−λ	, где λ = np . Эти значения	Pn (m) приведены в таблицах, для
	m!

применения которых надо лишь вычислить λ и знать m. Формула Пуассона получается из формулы Бернулли при n →∞.

P	(m)=Cm pmqn−m =	n!		λ m 1−		λ n−m	,
n	n
		m!(n −m)! n				n

26

Лекции 1-2

сократив на n! и (n −m)! , получим:

P (m)

P

(m)= (n −m +1) (n −m +2)

... n

λ m 1

− λ n

1−

λ −m

=

n

n

m!

n

n

n

λm (n −m +1)(n −m + 2)...n

λ n

λ

−m

=

1 −

1 −

=

m! n

m

n

n

=

λm

n −m +1

n −m +2

...

n

λ

−m

1 −

λ n

m!

n

n

n

1 −

n

.

n

При n →∞ каждая из дробей

n −m +1 ,n −m +2

,...,n

стремится к 1,

n

λ n

n

n

−

= e

−λ

lim 1

n→∞

n

(применяем

второй замечательный предел),

−

λ −m

lim 1

=1.

n→∞

n

Таким образом, получаем формулу Пуассона:

P	n	(m)≈ λme−λ	, где λ = np .
		m!

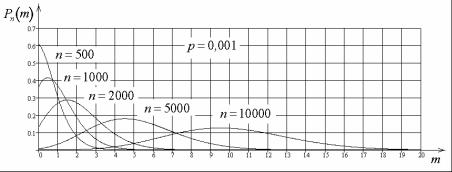
На рисунке приведены значения вероятности, вычисленные по формуле Пуассона для p = 0,001 и различных значений n. Смысл имеют значения только при целых m.