Metodika

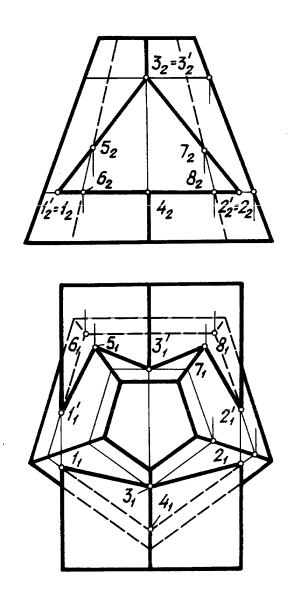
гательных плоскостей – отмечены профильные проекции 13, 23, З3, 43, 73, 83, 93, 103 искомых точек 1, 2, 3, 4, 7, 8, 9, 10 и по линиям связи найдены их фронтальные и горизонтальные проекции. Точки 5 и 6 пересечения верхнего ребра призмы с поверхностью пирамиды найдены по алгоритму первой позиционной задачи с помощью фронтальной плоскости уровня (см. задачу на рис. 27). Полу-

ченные вершины соединены в соответствии с приведенным выше правилом. Точки, принадлежащие нижней грани призмы и одновременно граням SAB, SBC, SCD, SAD после-

довательно соединенные отрезками прямых, образуют плоскую замкнутую ломаную линию 7–8–9–10–7. Ломаная 1–2–3–6–4–5–1 пересечения граней SAB, SBC, SCD, SAD пирами-

ды с гранями призмы является пространственной. Видимыми относительно какой-либо плоскости проекций являются звенья ломаной, являющиеся линиями пересечения двух видимых относительно соответствующих плоскостей проекций граней призмы и пирамиды. На основании этого видимыми относительно П2 являются звенья 5–4 и 4–6, а относительно П1 — все звенья ломаной, 1–2– 3–6–4–5–1. Если хотя бы одна из граней любого многогранника невидима относительно какой-либо плоскости проекций, то невидимы и принадлежащие ей звенья ломаной. Поэтому невидимы относительно П2 звенья 5–1–2–3–6, а относительно П1

— все звенья ломаной. 7–9–10–7.

На рис. 46 построена линия пересечения пятиугольной усеченной пирамиды с треугольной призмой, грани которой являются фронтально проецирующими плоскостями. Точки 5, 6, 7, 8 пересечения ребер пирамиды с гранями призмы найдены как точки пересечения прямой с проецирующей плоскостью, а точки 1, 1 , 2, 2 , 3, 3 пересечения ребер призмы с поверхностью пирамиды и точка 4 пересечения ребра пирамиды с поверхностью призмы — из условия принадлежности их поверхности пирамиды. Соединение вершин и определение видимости звеньев ломаных выполнено так же, как в предыдущей задаче.

41

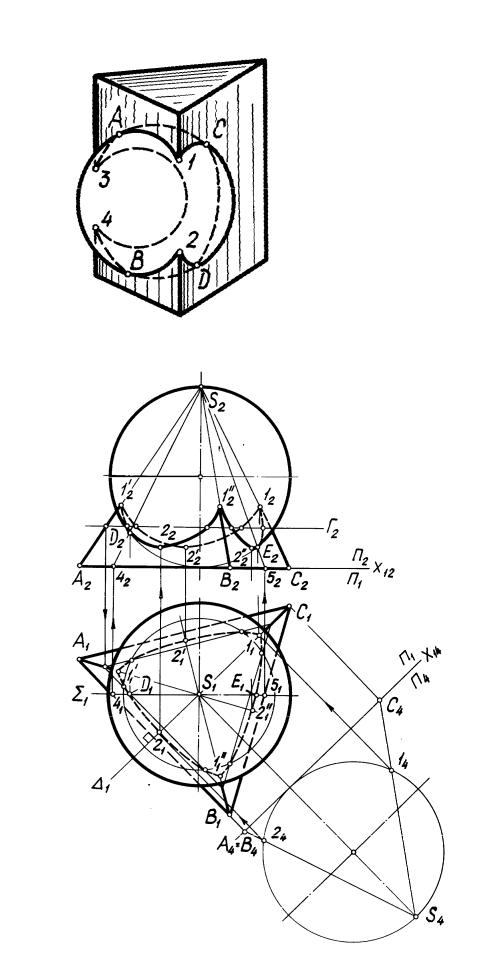
Рис. 47

Рис. 48

Задача 5. Построение линии пересечения многогранной и кривой поверхностей.

Линия пересечения многогранной и кривой поверхностей является совокупностью нескольких плоских кривых, каждая из которых — результат пересечения кривой поверхности с одной из граней многогранника (рис. 47). Эти плоские кривые попарно пересекаются в точках пересечения ребер многогранника с кривой поверхностью. В случае проницания эта совокуп-

42

ность плоских кривых распадается на две или более части. Построение каждой из этих кривых выполняется в соответствии с указаниями, данными в начале п. 2.2 данного параграфа. Алгоритмы построения опорных и промежуточных точек аналогичны рассмотренным в задачах 3 и 4, п. 2.1 и в задаче 3, п. 2.2 данного параграфа.

На рис. 48 построена линия пересечения правильной треугольной пирамиды SABC со сферой .

Для определения очерковых относительно П2 точек D и Е через ось вращения сферы проведена фронтальная плоскость уровня , пересекающая сферу по главному меридиану, а пирамиду — по треугольнику S–4–5 и т.д. по схеме. Построена фронтальная проекция S2–42–52 треугольника сечения и в пересечении ее с очерком фронтальной проекции сферы (проекцией главного меридиана) получены фронтальные проекции D2 и E2 искомых точек. Их горизонтальные проекции D1 и E1 найдены по линиям связи из условия принадлежности то-

Рис. 49

43

чек D и Е плоскости . Точки D2 и E2 являются точками смены видимости фронтальной проекции кривой.

Построение точки 1 пересечения ребра SC пирамиды со сферой выполнено с помощью плоскости : (SC П1) с использованием преобразования системы П2/П1 в систему П4/П1, в которой. плоскость является фронтальной плоскостью уровня (см. решение 1-й позиционной задачи 3, на рис. 29, б).

Плоскость является общей плоскостью. симметрии сферы Ф и грани SAB пирамиды. Поэтому точка 24 является проекцией на П4 низшей точки 2 линии пересечения грани SAB пирамиды и сферы Ф. Проекции 21 и 22 точки 2 построены обратным преобразованием.

Примечание. Так как пирамида SАВС правильная, и ее высота проходит через центр сферы, высоты точек 1 и 1 равны высоте точки 1, а высоты точек 2 и 2 — высоте точки 2.

На чертеже показано построение промежуточных точек с помощью горизонтальной плоскости уровня Г(Г2), пересекающей сферу по окружности, а пирамиду по треугольнику, подобному основанию. Точки пересечения этих линий

— искомые. При построении опорных и промежуточных точек линии пересечения использованы элементарные задачи 1,3, 4, 11, 19. Найденные точки соединены с учетом видимости плавными кривыми. Полученные проекции линии пересечения - совокупность частей эллипсов, являющихся проекциями трех дуг окружностей пересечения сферы с плоскостями общего положения (гранями

пирамиды). Видимой относительно П2			является часть кривой, расположенная
перед плоскостью , а относительно П1			вся кривая невидима, так как располо-
жена под плоскостью экватора сферы.
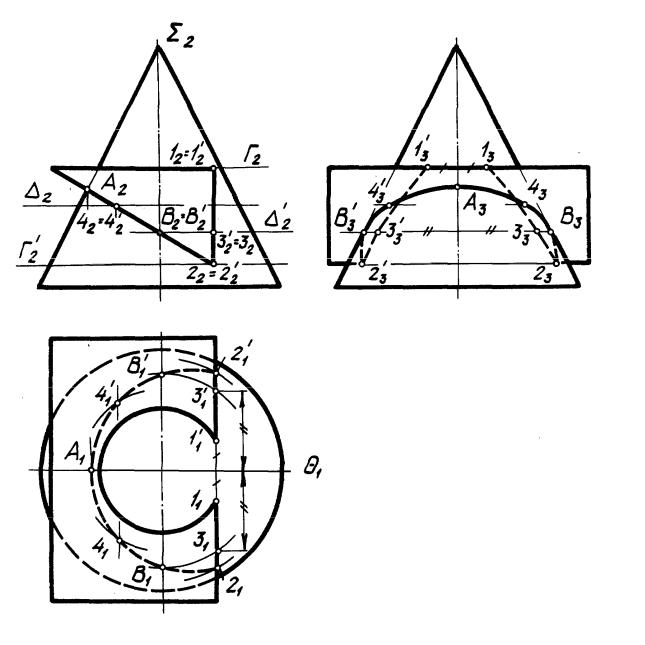
На рис. 49 построена линия пересечения поверхностей конуса и треуголь-
			ной призмы. Эта линия со-
			стоит из совокупности ду-
			ги окружности, части ги-
			перболы и части эллипса.
			Построение	точек	пересе-
			чения ребер призмы с по-
			верхностью пирамиды вы-
			полнено по алгоритму пер-
			вой позиционной		задачи
			(см. п. 2.1 данного пара-
			графа), опорные и проме-
			жуточные	точки	эллипса
			найдены так же, как в за-
			даче на рис. 39. Построе-
			ние промежуточных точек
			гиперболы,	выполненное с
			помощью	горизонтальной
	Рис. 50
			плоскости уровня , ясно

44

из чертежа. Видимы на П1 проекции линий, которые принадлежат видимым относительно П1 граням, а на П3 — проекции линий, принадлежащие видимым относительно П3 граням призмы и расположенных слева от профильной плоскости уровня .

Рис. 51 Так как грани призмы являются проецирующими плоскостями, задачу

можно решить на основании принадлежности точек линии пересечения граням призмы и кривой поверхности, т.е. многократно решить элементарную задачу 5.

45

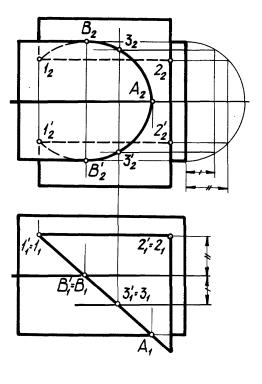
Так выполнено построение точек линии пересечения поверхностей цилиндра и призмы (рис. 50). Линия пересечения представляет собой совокупность эллипса, окружности и пары образующих. Видимость проекции линии на П2 определена на основании общих положений.

Задача 6. Построение линии пересечения двух кривых поверхностей. Линия пересечения двух кривых поверхностей (рис. 32) в общем случае

(случай врезки) представляет собой пространственную кривую, которая может распадаться не две или более части (случай проницания.). Точки этой линии (опорные и промежуточные) определяются при помощи основного способа построения линии пересечения поверхностей, изложенного в начале п. 2.2 по схеме, приведенной там же.

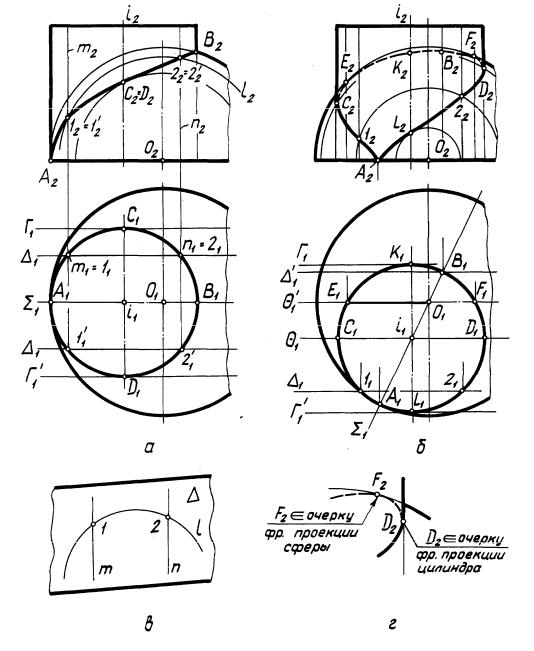
На рис. 51, а построена линия пересечения сферы Ф и цилиндра вращения. Построение опорных А, В, С, D и промежуточных 1, 1 , 2, 2 точек линии пересечения выполнено на основании общей схемы решения второй позиционной задачи по однотипному алгоритму (рис. 51, в):

1)2

2)l (окружность) m, n (прямолинейные образующие)

3)l m 1 l n = 2.

Экстремальные (низшая и высшая) точки А и В построены с помощью плоскости (рис. 51, а) — общей плоскости симметрии заданных поверхностей. Так как // П2, она пересекает обе поверхности по их главным меридианам. Поэтому фронтальные проекции А2 и В2 искомых точек, полученные как точки пересечения очерков фронтальных проекций поверхностей сферы и цилиндра, являются очерковыми одновременно для обеих поверхностей. Экстремальные точки С и D(наиболее и наименее удаленные от П2) определены с помощью плоскостей Г и Г . Так как кривая А–1–С–2–В –2 –D–1 –A симметрична относительно плоскости , фронтальные проекции ее видимой и невидимой частей совпадают (С2 = D2, 12 = 12 , 22 = 22 ).

Задача, на рис. 51, б, отличается от предыдущей только тем, что общая плоскость симметрии заданных поверхностей, проходящая через их оси вращения, не параллельна П2. Горизонтальные проекции А1 и В1 низшей и высшей точек линии пересечения найдены из условия принадлежности их плоскости и поверхности цилиндра, фронтальная проекция А2 — из условия принадлежности точки А поверхности сферы. Построение всех остальных точек (в том числе и высшей точки В) аналогично рассмотренному в задаче на рис. 51 а.

Очерковые точки С, D, E и F, принадлежащие соответственно главным меридианам цилиндра и сферы, построены с помощью плоскостей и . Точки С2 и D2 являются точками смены видимости фронтальной проекции кривой. Видимой относительно П2 является часть кривой, расположенная перед плоскостью . На рис. 51, г в увеличенном масштабе показано расположение очерковых точек F2 и D2 и видимость проекции кривой и очерков фронтальных проекций поверхностей.

46

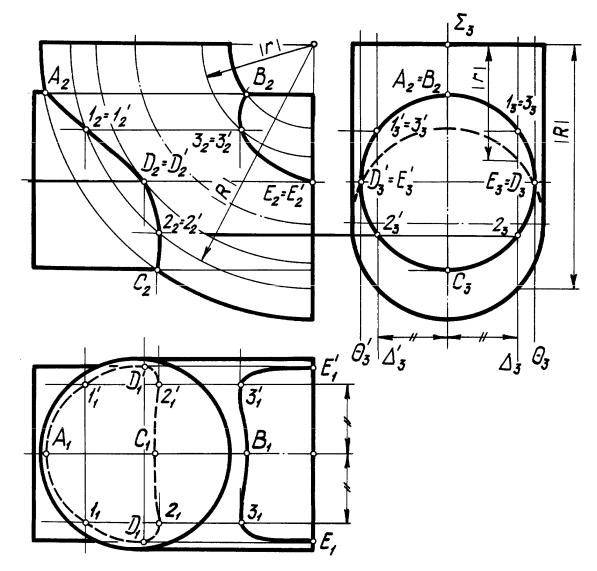
Рис.52

В задаче на рис. 52 решение выполнено с помощью фронтальных плоскостей уровня , на основании общей схемы решения второй позиционной задачи. Алгоритм определения опорных и промежуточных точек составьте самостоятельно.

Задача на рис. 53 решена на основании принадлежности точек линии пересечения поверхностям цилиндра и конуса, т.е. сведена к многократному решению элементарной задачи 8, так как горизонтальная проекция линии пересечения задана т. е. совпадает с горизонтальной проекцией цилиндра.

На рис. 54 показано построение линии пересечения поверхностей конуса вращения и наклонного цилиндра вращения способом концентрических сфер.

Очерковые относительно П2 точки А и В (они же высшая и низшая) определены с помощью общей, плоскости симметрии // П2. Применение вспомогательных плоскостей для построения других точек не дает графически простого решения.

Так как оси заданных поверхностей вращения пересекаются и параллельны П2 (принадлежат общей плоскости симметрии ), качестве вспомогательных

47

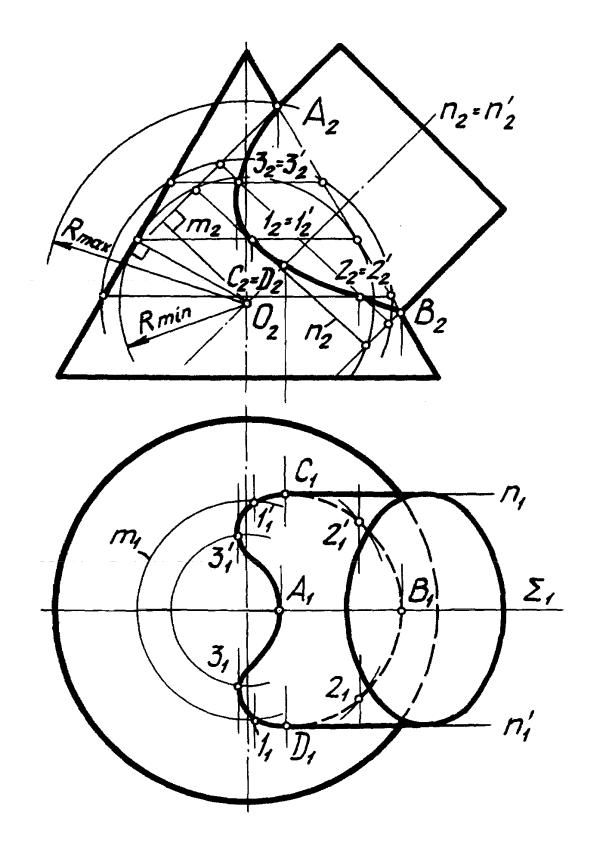
поверхностей могут быть выбраны сферы с общим центром в точке О пересечения осей заданных поверхностей. Эти сферы соосны с каждой из поверхностей и пересекаются с ними по окружностям. Построение выполняется на основании общей схемы решения второй позиционной задачи по однотипному алгоритму:

1)Rmin R Rmax), – сфера;

2)m k, – m, k – окружности;

3)m k = 1,1 .

Графическая реализация алгоритма показана на рис. 54. Окружности m и k проецируются на П2 в виде отрезков прямых[m2] и [k2], так как плоскости этих

12 пе-

екциями

полагаются

видимости n и n

потора ажено П2 точнтальвспо-

определения

дущем ого реностей применеверхнозаданные

симмогут одноокружно-

О , ...),

ках оси вспомогаре-

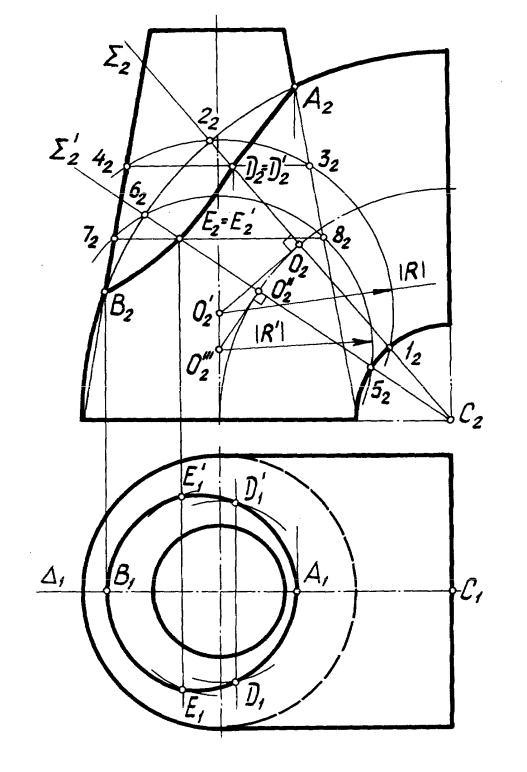
Для нахождения центров вспомогательных сфер отмечены фронтальные проекции [12-22] , [52-62] окружностей m, n сечения тора плоскостями, , проходящими через ось тора. Искомые центры находятся в точках, например, О, пересечения перпендикуляров к плоскостям этих окружностей, проведенных через их центры, например, через О , с осью конуса вращения. Построение всех промежуточных точек выполняется по однотипному алгоритму.

1)R) — сфера;

2)= m, = n, m и n — окружности;

3)m n = D, D .

Дальнейшее ясно из чертежа.

Рис.55

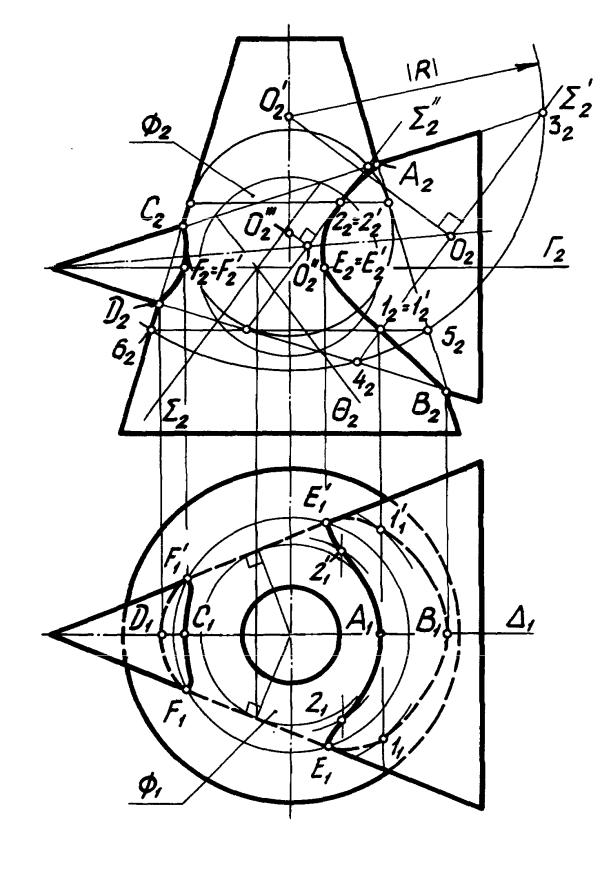
Рис. 56 На рис. 56 показано применение способа эксцентрических сфер для по-

строения линии пересечения эллиптического конуса и конуса вращения. Пред-

50