tensor

Свертка

Мы уже отметили свертку – на примере квадрата длины вектора: простейшая свертка это скалярное произведение. Рассмотрим вопрос подробнее.

Свертка возникает при записи перемножения, когда один из индексов повторяется сверху и снизу. Так произведение:

Aik Bimn = Ck mn – будет иметь не 5-й, а 3-й ранг: при однократной свертке ранг понижа- ется на 2. Здесь свертка идет по индексу i.

Вспомнив, что повторяющийся индекс означает суммирование, запишем нашу сверт- ку детально:

Aik Bimn = å Aik Bimn = A1k B1mn + A2k B2mn + A3k B3mn . i

Здесь видно, каким образом пропадает немой индекс i.

Свертка тензора 2-го ранга внутри себя называется следом тензора, специалисты ста- рой школы предпочитают немецкий эквивалент: шпур (Spur). Так квадрат длины x2 = xi xi

это след (шпур) тензора Xii = xi xi . По сути дела это сумма элементов его главной диагонали.

Очевидно, что след, как любой скаляр – инвариант.

Инвариант тензора

Мы знаем, что инвариантом вектора является его длина, выражающаяся через свертку вектора с ковектором. А что с тензором большего ранга?

Любой тензор имеет инвариант (скаляр), получающийся сверткой с сопряженным тен- зором. Например, инвариантом тензора второго ранга, дважды контравариантного: Aik – бу- дет, очевидно, выражение: Aik Aik .

На этом можно бы закончить… Но, ради полной ясности, все-таки распишем, что та- кое двойная свертка. Сначала свертываем, например, по индексу i:

Aik Aik = A1k A1k + A2k A2k + A3k A3k .

Вторым шагом свертываем по k каждый из трех получившихся членов:

Aik Aik = (A11 A11 + A12 A12 + A13 A13 ) + (A21 A21 + A22 A22 + A23 A23 ) + (A31A31 + A32 A32 + A33 A33 ) .

Что полученное громоздкое выражение является инвариантом, ничуть не «очевид- но»… Но мы в этом уверены! Просто потому, что в результате двойной свертки все индексы пропадают. Следовательно, обязан получиться скаляр.

Выполнение простых правил оперирования индексами избавляет от трудоемких дока- зательств.

Разумеется, инвариантом комбинированного тензора Aik будет величина Aik Aki .

Метрический тензор

Завершив затянувшийся экскурс в общие вопросы, возвращаемся к тому, с чего все началось – к формуле для длины вектора:

x2 = x x1	+ x x2	+ x x3 .	(1.3)
1	2	3

Сейчас мы умеем записать ее в сокращенном виде:

x2 = x xi .	(1.3а)
i

Вспомним теперь, что:

11

x = g	ik	xk .	(1.5)
i

Подставляя в (1.3а), имеем:

x2 = gik xi xk .

(1.6)

Это общий вид тензорного выражения для длины, использующее контравариантные (естественные) компоненты.

Тензор gik есть метрический тензор пространства. Метрический тензор это как бы правило вычисления длины любого вектора по значениям его компонент. Применительно к (1.5) говорят, что здесь вектор xi свертывается с метрическим тензором и получается век- тор xi . То есть метрический тензор это еще и способ преобразования компонент – от контра- вариантных к ковариантным и наоборот.

Теперь для длины вектора мы теперь имеем ряд вариантов (на выбор): x2 = xi xi ;

x2 = gik xi xk ;

x2 = gik xi xk .

Аналогично для скалярного произведения: xy = xi yi ;

xy = gik xi yk ;

xy = gik xi yk .

Свойства метрического тензора

Мы не утруждали себя вычислением составляющих метрического тензора, и потому кажется, что про их значения ничего сказать нельзя. Но это не так.

Во-первых, вспомним, что коэффициенты в выражении для длины мы (из соображе- ний симметрии) вводили так, что gik = gki . Вот вам и первое свойство метрического тензора:

его матрица симметрична (элементы, симметричные относительно главной диагонали, оди- наковы).

Далее, в декартовых координатах x2 = (x1)2 + (x2 )2 + (x3 )2 , то есть, между xi и xi нет разницы. Делаем второй вывод: именно здесь метрический тензор выглядит крайне просто:

é1	0	0ù
ê	1	ú	(1.7)
gik = ê0		0ú .
ê	0	ú
ë0		1û

Члены со смешанными индексами (i ¹ k) в выражение для длины не входят. Итак,

метрический тензор для случая прямоугольных координат является диагональной матрицей, причем все элементы главной диагонали равны единице.

Единичный тензор

Полезным понятием является единичный тензор, обозначаемый символом Кронекера δik . Он определяется так:

δik xi = xk

(1.8)

12

– для любого вектора х. Единичный тензор как бы выделяет желаемую (k-ю) компо- ненту вектора.

Слева записана сумма – раскроем ее:

δik xi = δ1k x1 + δ2k x2 + δ3k x3 = xk .

Для выполнения равенства нужно, чтобы равнялась единице только та компонента δik , для которого i = k . А остальные должны быть нулевыми. Значит, единичный тензор вы- глядит точно как (1.7)!

Перейдем к другой системе координат, компоненты вектора изменятся. И единичного тензора тоже… Но то, что мы разъяснили относительно (1.8), остается, тем не менее, в силе!

Получается, что тензор δik обладает редким свойством: его компоненты одинаковы в любой системе координат, не изменяются.

Физические векторы

Мы рассматривали вектор перемещения – он имеет чисто геометрическую природу.

А теперь рассмотрим в качестве примера вектор скорости. Чтобы получить компонен- ты, надо представить его в виде линейной комбинации ортов пространства… но вот беда: орты имеют у нас другую размерность – размерность расстояния, а не скорости!

Впрочем, ведь мы имеем выражения, связывающие различные физические величины с перемещением. Так, скорость определяется:

vi = dx	i	æ	1	, dx	2	, dx	3	ö	= (v1, v2 , v2 ) .
		= ç dx						÷
dt		ç	dt	dt		dt		÷
		è						ø

Скорость это вектор потому, что дифференцирование – линейная операция. А время t в нерелятивистской механике рассматривается как скаляр: оно инвариантно.

Компоненты вектора скорости в принятом базисе, разумеется, контравариантны. Аналогично вводится контравариантный вектор ускорения:

æ	1	, dv	2	, dv	3	ö	= (a1, a2 , a3 ) .
ai = ç dv						÷
ç	dt	dt		dt		÷
è						ø

Рассмотрим вектор силы. Из формулы, связывающей ее с ускорением, имеем: f i = mai = (ma1, ma2 , ma3 ).

Здесь вектор силы оказывается в контравариантных компонентах, поскольку индекс i справа контравариантный.

Однако запишем формулу для силы в потенциальном поле: f = k gradϕ (коэффициент k зависит от природы поля).

А теперь вспомним, что вектор градиента ¶¶xϕ1 , ¶¶xϕ2 , ¶¶xϕ3 ковариантен в базисе, в кото-

ром задано поле! Это видно и формально – из того, что контравариантные компоненты стоят в знаменателе. Значит, и вектор силы получается здесь в ковариантных компонентах:

	¶ϕ		æ	¶ϕ		¶ϕ			¶ϕ		ö
fi = k			= çk		, k			, k			÷ .
	¶x	i		1		¶x	2		¶x	3
			è	¶x							ø

Приравнять его к mai будет формально неправильным. Придется свернуть с метриче- ским тензором пространства, получив корректное соотношение:

13

k ∂∂xϕi gik = mak .

Разумеется, в декартовых координатах такое усложнение излишне.

14

2.Тензоры в релятивистской механике

Вфизике, в отличие от геометрии, существенно присутствует время, движение. В час- ти перехода между системами координат – интерес представляют не столько системы с вза- имно повернутыми осями, сколько системы, взаимно движущиеся.

Тензорный стиль формулировки специальной теории относительности вызван некото- рой причиной: пространственная длина (в понимании, имеющем физический смысл) оказалась неинвариантной – при переходе к другой, движущейся системе координат. Это след- ствие опытов.

И в то же время опыты показывают, что физические законы действуют в указанных системах одинаково. Значит, законы должны допускать формулировку в тензорной форме, из которой, как положено, вытекают некоторые инварианты – относительно переходов между движущимися системами координат.

Пространство СТО

Выяснилось, что инвариантом является интервал. Он (точнее, его квадрат) опреде- ляется следующим образом:

s2 = (ct)2 - x2 - y2 - z2 = (ct)2 - r2 .

(2.1)

Система координат x, y, z здесь декартова, а с – фундаментальная константа, имею- щая размерность скорости. И, соответственно, являющаяся инвариантом.

Трехмерный вектор r по-прежнему выражает пространственную дистанцию, а вели- чина ct – временнýю. В целом скаляр s выражает «расстояние» – но не между пространст- венными точками, как ранее, а между пространственно-временными. То есть между собы-

тиями.

Эти краткие сведения приведены здесь с целью напомнить, а вообще-то предполага- ются известными.

Метрика 4-пространства

Форма (2.1) содержит, как видно, четыре квадратичных члена. Удобно приписать ее четырехмерному пространству событий – пространству Минковского с координатами:

ct, x, y, z . Применим обозначение: x0 , x1, x2 , x3 , и тогда:

s2 = (x0 )2 - (x1)2 - (x2 )2 - (x3)2 .

(2.1б)

Но ведь в общем виде квадрат длины записывается:

s2 = g00 (x0 ) + g11(x1)2 + g22 (x2 )2 + g33 (x3 )2 (члены со смешанными индексами у нас от- сутствуют). Сравнивая с (2.1б), где фигурируют минусы, получаем для 4-мерного метриче- ского тензора:

g00	=1,	g11 = g22		= g33 = -1 (остальные компоненты нулевые). В матричной форме:
	é1	0	0	0	ù
	ê	-1			ú
gik	= ê0		0	0	ú	. Перед вами метрический тензор 4-пространства.
	ê	0	-1	0	ú
	ê0				ú
	ë0	0	0	-1û

Если бы все элементы главной диагонали метрического тензора равнялись 1, разницы между ковариантным и контравариантным представлением не было бы. В наших же коорди-

15

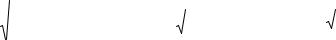
натах (их называют галилеевыми) это совсем не так. Потому и приходится брать в соображе- ние тензорные примочки.

Выразим интервал через координаты 4-вектора:

s2 = (x0 )2 − (x1)2 − (x2 )2 − (x3 )2 = x0 x0 − x1x1 − x2 x2 − x3x3 .

Приведем это к стандартной форме для длины:

s2 = xi x = x0 x	0	+ x1x + x2 x	2	+ x3x	(2.2)
i		1		3

Как всегда, квадрат длины это скалярное произведение вектора на ковектор.

Дифференциал интервала

Нам будет полезно выражение для дифференциала интервала. Из (2.2) очевидно:

ds2 = dxidx = dx0dx + dx1dx + dx2dx

+ dx3dx .

(2.2а)

i

0

1

2

3

Простыми преобразованиями получаем:

ds = dt c2 − dx2

− dy2

− dz2 = dt

= cdt

.

c2

− v2

− v2

− v2

1− v2 /c2

(2.3)

dt2

dt2

dt2

x

y

z

Формула (2.3) не раз потребуется. Использованные обозначения, кажется, понятны без пояснений. Следует лишь оговорить, что v – не есть скорость какого-то конкретного объ- екта. Это просто отношение приращения линейного промежутка между событиями (беско- нечно близкими) к временному промежутку, имеющее размерность скорости. Поэтому впол- не возможно, что v > c . Просто это будет соответствовать мнимому интервалу – как говорят,

пространственноподобному.

Четырехвекторы

Итак, контравариантный геометрический вектор xi от события А к событию В имеет компоненты: x0 , x1, x2 , x3 . Здесь первую (точнее, нулевую) компоненту x0 = ct называют

временнóй, остальные – пространственными. xi это вектор в четырехмерном пространстве (правда, не эвклидовом, а псевдоэвклидовом), как говорят – 4-вектор.

Вообще у любого 4-вектора СТО, какое бы физическое содержание он ни имел, нуле-

вую компоненту называют временной. Три остальные компоненты называют про-

странственными. В совокупности последние образуют трехмерный вектор. Что принято ус- ловно изображать так: xi (x0, x) .

Конечно, трехмерный вектор х уже не имеет тензорных свойств относительно перехо- да между движущимися системами координат (не инвариантен).

Подчеркну: трехмерный вектор не сохраняет свои компоненты при переходе меж-

ду системами координат (если только это не трехмерный поворот). Изменяется временная компонента 4-вектора – значит, обязана измениться хотя бы одна пространственная.

Сопоставляя s2 = x0 x0 − x1x1 − x2 x2 − x3x3 и s2 = x0 x0 + x1x1 + x2 x2 + x3x3 , выводим 4- вектор в ковариантных компонентах:

xi (x0 , x1, x2 , x3 ) , где x0 = x0 , x1 = −x1 , x2 = −x2 , x3 = −x3 .

Как видим, для преобразования к ковариантным компонентам и обратно надо лишь поменять знаки перед всеми компонентами, кроме нулевой. Проверьте, что со-

блюдается классическое: xi = gik xk .

Между прочим, это позволяет установить, как выглядит в СТО дуальный базис (тот самый, в котором векторы приобретают свои ковариантные компоненты). Он отличается от

16

главного базиса просто сменой направлений пространственных осей на противоположные (а временная ось не меняется).

Преобразования координат

Компоненты 4-вектора при переходе к другой (движущейся со скоростью v) системе координат обязаны изменяться таким образом, чтобы квадрат вектора (квадрат интервала) оставался неизменным. Для простоты примем c = 1, и тогда данное требование запишется:

t'2 -x'2 -y'2 -z'2 = t2 - x2 - y2 - z2 .

Легко проверить (простой подстановкой), что этому условию удовлетворяют преобра- зования:

x'=

x - v

t

, y'=

y − vyt

, z'=

z - v

t

, t'=

t - vr

.

(2.4)

x

z

1

- v2

1- v2

1- v2

1- v2

Они называются преобразованиями Лоренца.

Запишем преобразования в более привычном виде:

x'=			x - vt	, y'= y , z'= z , t'=	t	- vx / c2	.	(2.5)
1			- v2 / c2		1- v2 / c2

Подобная запись допустима: всегда можно повернуть оси координат таким образом, что относительная скорость систем координат будет направлена вдоль оси Х.

Внимание: в точности по этим же формулам преобразуются компоненты вообще любого 4-вектора СТО xi (примеры их мы рассмотрим далее). Только, с учетом того, что x0 = ct , формулы записывают в общем виде так:

	1				v		0																0		v	1
		x		-		x															x				- c x
1					c			, x'	2	= x	2	,	x'	3	= x	3	,		0									.	(2.5а)
x'	=																	x'		=
	1			- v2 / c2																1				- v2 / c2

Четырехскорость

Перейдя к четырехмерным формулировкам, мы отказались рассматривать чисто про- странственное перемещение. Тогда и обычная скорость нас тоже не устраивает! В самом де-

	dr æ dx				dy		dz ö
ле, в v =		ç		,		,		÷ время уже не является инвариантной переменной, одинаковой в
	dt				dt
		è dt					dt ø

любой системе координат. Теперь время это просто одна из координат 4-вектора перемеще- ния. То есть не скаляр!

Чтобы получить 4-векторную величину, аналогичную скорости, следует дифференци- ровать по некоторой другой переменной, инвариантной в 4-пространстве – скаляру. Такой величиной является интервал.

Из указанных соображений вектор 4-скорости определяют так:

u

i

=

dxi

.

(2.6)

ds

Из

соотношения

(2.2а)

ds

2 = dx0dx

+ dx1dx + dx2dx

2

+ dx3dx выводим (поделив на

0

1

3

ds2 ):

dx0

dx

+

dx1

dx

+

dx2

dx

+

dx3

dx

=1.

ds

0

ds

1

ds

2

ds

3

ds

ds

ds

ds

Учитывая (2.6), имеем:

17

u0u0 + u1u1 + u2u2 + u3u3 = 1.

То есть длина вектора 4-скорости всегда равна единице. Странно? Ничуть, так и долж- но быть, длина любого 4-вектора это скаляр, инвариант. Кстати, 4-скорость – величина без- размерная (ведь интервал имеет размерность пространственного расстояния).

Можно выразить компоненты 4-скорости через привычные трехмерные величины:

	u0 =	d(ct)	=	1			– тут просто использовано (2.3). Теперь v уже реальная ско-
		ds
				1- v2 / c2

рость, ведь мы рассматриваем пространственный и временной промежутки, характеризую- щие движение заданного тела.

Столь же легко получаем:

u1 =

v

x

, u2 =

vy

, u3

=

v

z

.

c 1

- v2 /c2

c 1- v2 /c2

c 1- v2 / c2

Три пространственные компоненты можно объединить в трехмерный вектор:

i

0

æ

1

v

ö

u

ç

÷

(2.6а)

,

= (u , u) = ç

1- v

2

/ c

2

c 1

- v

2

/ c

2

÷ .

è

ø

4-вектор энергии-импульса

Известное из школы выражение для импульса тела: p = mv (m – масса) является трех-

мерным, и, следовательно, неивариантным: абсолютная величина импульса при переходе к движущейся системе координат не сохраняется. Чтобы получить четырехмерную конструк- цию, на место скорости ставим 4-скорость. Ну а с массой все в порядке: это скаляр.

Впрочем, возможно, вы читали, что масса движущегося тела возрастает? Это архаич- ный взгляд, о котором пора забыть…

4-скорость имеет другую размерность, чем просто скорость. Поэтому для преемствен- ности домножают еще на с. В итоге для импульса имеем:

pi = mcui .

Так как uiui =1, то: pi pi = m2c2 (инвариантный квадрат 4-вектора pi ).

Подставив компоненты 4-скорости, легко расписываем компоненты

4-импульса:

p0 =

mc

, p1 =

mv

x

, p2 =

mvy

, p3

=

mv

z

.

1

- v2 / c2

1

- v2 / c2

1- v2 / c2

1- v2 / c2

Ну и, как всегда, пространственные компоненты можно объединить под эгидой трех- мерного вектора:

i

0

æ

mc

mv

ö

ç

÷

(2.7)

p = ( p , p) = ç

1- v

2

/c

2 ,

1- v

2

/ c

2

÷ .

è

ø

При малых скоростях имеем привычную формулу:

p =			mv	» mv .
1			- v2 / c2

Мы без труда получили две вещи:

1) релятивистскую формулу для трехмерного импульса: p =

		mv		;
	1- v2 / c2

2) 4-вектор импульса, имеющий еще и некоторую загадочную временную компонен- ту. Займемся ею.

18

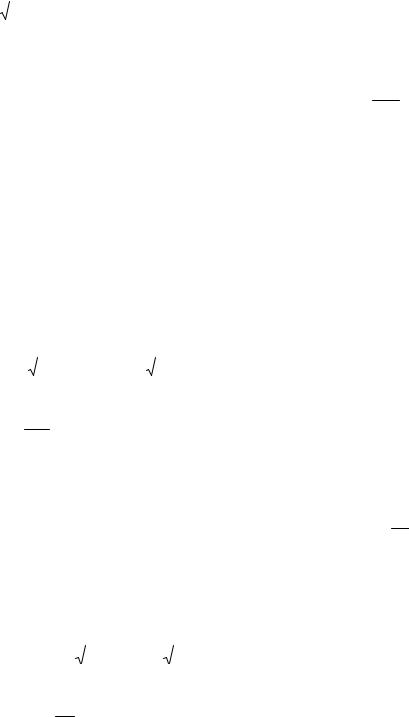
При малых скоростях данная составляющая равна:

mc

æ

v

2

ö

= mc + mv

2

= 1

æ

+ mv

2

ö

» mcç1

+

÷

çmc2

÷ .

2

1- v2 / c2

ç

2c

÷

2c

c

ç

2

÷

è

ø

è

ø

В скобках оказалась полная энергия E , состоящая из двух слагаемых:

1)энергия покоя, равная mc2 ;

2)кинетическая энергия (для малых скоростей равная mv2 2 ).

Теперь окончательно ясен физический смысл компонент 4-вектора импульса. Это полная энергия (с точностью до коэффициента) и три компоненты импульса:

pi (E / c, p).

Отсюда название: 4-вектор энергии-импульса.

Напомню, что квадрат его равен m2c2 . То есть:

	E2	- p2 = m2c2 .	(2.8)
	c2

Без труда мы получили фундаментальное уравнение релятивистской динамики. Сопоставляя два члена в (2.7):

E	=		mc	и p =			mv	,
c
		1- v2 /c2		1			- v2 / c2

получаем и вторую важную формулу:

E = pcv 2 .

4-сила

Ее можно ввести по аналогии с трехмерным случаем f = ddtp . Но для 4-вектора прини-

маем уже:

f

i

= dpi

. Как и ранее, используя (2.3), легко получается:

ds

i

æ dE

1

f

ö

f

=

ç

÷

(2.9)

ç

c

2

1- v

2

/ c

2 ,

c 1

- v

2

/ c

2

÷ .

è dt

ø

Здесь, как всегда, f это обычный трехмерный вектор силы.

Кстати, ddtE = fv это мощность, вот вам и физический смысл нулевой компоненты 4-

силы!

Теперь подставим в f i = dpi определение 4-импульса: pi = mcui . Получим: ds

	f	i	= mc	dui	.	(2.10)
				ds
	Перед нами					аналог знакомой формулы: f = ma = m	dv	. Производная	dui	это 4-
							dt		ds

ускорение. А множитель с появляется в связи с уравниванием размерностей.

19

Еще раз увидели, как знакомые трехмерные векторы превращаются в 4-векторы. А в качестве нулевой компоненты последнего выступает некоторый «скаляр». В кавычках, пото- му что в 4-пространстве он скаляром не является.

Дифференцирование по координатам

В физике рассматриваются скалярные и векторные поля и их производные – применя- ется аппарат векторного анализа. Поскольку поле зависит от четырех координат, речь идет о

частных производных.

Для того, чтобы образовывать инвариант, производные по координатам должны со- ставлять тензор. Запишем тензор производных векторного поля Ai :

		é	¶A1		¶A2		...ù
		ê		1	¶x	1	ú
¶A		ê	¶x			2	ú
		ê	¶A		¶A		ú
	i	= ê		1			...ú .
¶x	k		¶x	2	¶x	2
		ê					ú
		ê ...			...		...ú
		ë					û

Очевидно, что это смешанный (один раз контравариантный, один раз ковариантный) тензор второго ранга.

С его помощью можно выразить дифференциалы компонент 4-вектора:

i		¶Ai		k
dA	=		dx		.	(2.11)
		¶xk

Надеюсь, уже можно опускать надоевшее напоминание, что мы на самом деле имеем здесь сумму – в сокращенной записи.

Правда, логично задаться вопросом, действительно ли таблица частных производных это тензор. И если нет, то dAi уже не являются компонентами вектора…

В самом начале мы принимали, что при переходе к другому базису – новые значения компонент выражаются из старых просто линейными функциями, согласно (1.1). Но это не- справедливо в случае криволинейных координат!

В искривленном пространстве ¶Ai и dAi это уже не тензоры. Чтобы составлять тен-

¶xk

зорные выражения, требуется вносить некоторые поправки, зависящие от геометрической кривизны пространства.

Такие поправки называются символами Кристоффеля. И оказывается, что они же ха- рактеризуют гравитационное поле! Впрочем, здесь мы вступаем уже в сферу теории грави- тации, чего в данном популярном очерке делать не собирались…

20