Раздел VI. Числовые ряды

Глава 13. Числовые ряды

13.1. Понятие числового ряда. Сумма ряда.

Пусть задана бесконечная последовательность чисел .Выражение (1) называетсячисловым рядом.Числа называются членами ряда. Сумма конечного числаnпервых членов ряда называется-ой частичной суммой ряда: .

Рассмотрим частичные суммы: ,,,. Если существует конечный предел, то егоназывают суммой ряда (1)и говорят,что ряд сходится.Еслине существует,то ряд расходится и суммы не имеет.

Рассмотрим геометрическую прогрессию: . Первый член, знаменатель. Суммаnпервых членов.

1) Если , топрии- ряд сходится.

2)Если, топриине существует– ряд расходится.

3) , ради ряд расходится.

4), рад= 0 причетном,=принечетном, поэтомупредела не имеет,ряд расходится.

Геометрическая прогрессия с исходится,если.

Теорема 1.Если сходится ряд, полученный из данного ряда (1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, полученный из данного отбрасыванием нескольких членов.

Пусть - суммапервых членов ряда (1),- суммаотброшенных членов,- сумма членов ряда, входящих в суммуи не входящих в. Тогда, где- постоянное число, не зависящее от. Если существует, то существует и; если существует, то существует и, что и доказывает теорему.

Теорема 2. Если рядсходится и его сумма равна, то рядтоже сходится и его сумма равна.

Теорема 3. Если рядыисходятся и их суммы равны соответственнои, то рядыитоже сходятся и их суммы равныисоответственно.

13.2. Необходимый признак сходимости рада.

При исследовании рядов одним из основных вопросов является вопрос о сходимости ряда.

Теорема.Если ряд сходится, то его -й член стремится к нулю при неограниченном возрастании.

Пусть ряд u₁+u₂+u₃+u₄+…+u_n+… сходится, т.е.– сумма ряда. Тогда. Вычтем из одного другое:,, но,

Следствие.Если, то ряд расходится

Пример. Рядрасходится, т.к.. Это признак необходимый, ноне достаточный.

Рассмотрим гармонический ряд:. Хотя, но ряд расходится. Докажем это.. Напишем вспомогательный ряд:. Обозначимсуммупервых членов гармонического ряда и- вспомогательного ряда. Т.к. каждый член первого ряда больше соответствующего члена второго ряда (или равен ему), то для:. Подсчитаем частичные суммы второго ряда для;;;и т.д. Очевидно, что. Тогда, тогда,т.е. гармонический ряд расходится.

13.3. Признаки сравнения рядов

Пусть имеем два ряда с положительнымичленами:(2) и(3).

Теорема 1.Если члены ряда (2) не больше соответствующих членов ряда (3), т.е.и ряд (3) сходится, то сходится и ряд (2).

Пусть и-сумма рядов. Изследует, что. Т.к. ряд (3) сходится, то. Т.к. члены рядов положительны, то, тогда. Доказали, что частичные суммывозрастают и ограничены, значит, они имеют предел:и.

Пример.Рядсходится, т.к. его члены меньше соответствующих членов ряда. Последний ряд сходится, т.к. начиная со второго члена - это геометрическая прогрессия с.

Теорема 2.Если члены ряда (2) не меньше соответствующих членов ряда (3), т.е., и ряд (3) расходится, то и ряд (2) расходится.

Из условия следует, что(положительный ряд). Т.к. ряд (3) расходится, то, тогда изследует, что, т.е. ряд (2) расходится.

Пример.Рядрасходится, т.к его члены начиная со второго, больше соответствующих членов гармонического ряда, который расходится.

Теорема 3.Если существует конечный и отличный от нуля предел, то ряды (2) и (3) сходятся или расходятся одновременно.

13.4. Признак Даламбера.

Теорема.Если в ряде с положительными членамиотношениеприимеет конечный придел, т.е., то ряд сходится в случаи, ряд расходится при. Притеорема не дает ответа о сходимости ряда.

Доказательство.Пусть. Рассмотрим число:. По определению пределаначиная с номера, отсюда. Запишем последнее неравенство для:;;….

Рассмотрим два ряда: (1) и. Ряд– геометрическая прогрессия с- сходится. Члены ряда (1), начиная с, меньше членов ряда, поэтому ряд (1) сходится на основании признака сравнения.

Пусть . Тогда изследует, чтодля. Но это означает, что члены ряда возрастают ине стремится к 0, поэтому ряд расходится.

Замечание 1.

1. Если , то ряд расходится.

2. Если , но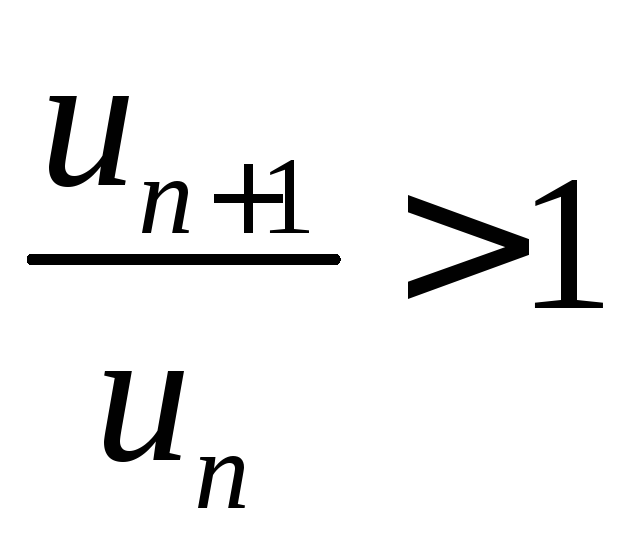, начиная с, то ряд расходится.

Пример.,:,- сходится.

Пример.,(- расходится).

Пример,,, то расходится, т.к..

Пример.,. Заметим, что, тогда данный ряд запишется:. Частичная суммапервых членов, тогда- ряд сходится и.

13.5. Признак Коши.

Если для ряда с положительными членами (1) величинаимеет конечный пределпри, т.е., то приряд сходится, а при– расходится.

1. Пусть . Рассмотрим. Начиная с:, или, или, для всех. Рассмотрим два ряда:(1) и. Рядсходится – геометрическая прогрессия с. Члены ряда (1), начиная с, меньше членов рядаряд (1) сходится.

2. Пусть , тогданачиная с, или– ряд расходится, т.к.не стремится к нулю.

Пример.,– сходится.

Замечание: Если, то требуется дальнейшие исследования.

Пример. Для гармонического ряда (), однако ряд расходится.

Пример,,, но ряд сходится, т.к. члены ряда, начиная со второго, меньше членов сходящего ряда.

13.6. Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, т.е., и пусть- такая непрерывная невозрастающая функция, что;, …,. Тогда ряди несобственный интегралсходятся или расходятся одновременно.

Построим графики членов ряда:

у

1 2 3 n n+1

Из графика (а) следует, что площади прямоугольников равны ;;; и т.д. и. С другой стороны, площадь области, ограниченной кривойи прямыми,,, равна, поэтому(1).

Из рисунка (б) следует, что сумма площадей всех прямоугольников равна , или(2).

Предположим, что сходится, тогда, т.е.остается ограниченной, т.е..

Пусть расходится, тогданеограниченно возрастает при увеличении. Тогда (из неравенства (1))тоже неограниченно возрастает, т.е. ряд расходится.

Пример. Ряд Дирихле:,- сходится,– расходится.

13.7. Знакочередующиеся ряды.

Члены знакочередующегося ряда имеют чередующиеся знаки: , где- положительны.

Теорема Лейбница.Если в знакочередующемся ряде(1): члены таковы, что(2) и(3), то ряд (1) сходится, его сумма положительна и не превосходит.

Рассмотрим сумму первых членов ряда (1):. Из (2) следует, чтои возрастает с увеличением. Запишем. В силу (2) каждая скобка положительна. В результате вычитаний получим число, меньше, т.е..возрастает и ограниченна сверху, поэтому имеет пределS:,. Рассмотрим нечетные суммы::,, то- (1) сходится.

Замечание.Теорема Лейбница справедлива, если (2) выполняется, начиная с некоторогоN.

Пример. Рядсходится:.

13.8 Знакопеременные ряды

Знакопеременные ряды– если среди членов есть положительные и отрицательные.

Числа - положительные и отрицательные.

Теорема.Если знакопеременный ряд(1) таков, что ряд из модулей(2) сходится, то и данный ряд сходится.

Доказательство.Пустьи- суммы первыхnчленов рядов (1) и (2).

Пусть - сумма положительных членов,сумма модулей отрицательных членов, тогдаи. По условиюимеет предел– положительные возрастающие величины, меньшие, поэтому они имеют пределыи, тогда иимеет предел, т.е. (1) – сходится.

Пример.. Рассмотрим ряди ряд(который сходится). Члены рядане больше соответствующих членов ряда, он также сходится, тогда, в силу доказанной теоремы, ряд сходится.

Пример.. Рассмотрим ряд. – геометрическая прогрессия – сходится. Сходится и заданный ряд.

Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов(2). Если ряд (1) сходится, а ряд (2) расходится, то знакопеременный рядсходится условно.

Пример.Рядсходится условно, т.к. рядрасходится.

Пример.есть абсолютно сходящийся ряд, т.к. ряд, состоящий из модулей, сходится.

Отметим следующие свойства абсолютно и условно сходящихся рядов.

1. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

2. Если ряд сходится условно, то, какое бы ни выбрали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась равной А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки окажется расходящимся.

Пример. Знакопеременный ряд(1) сходится условно. Обозначим его сумму,. Сделаем перестановку членов этого ряда так, чтобы за одним положительным членом следовали два отрицательных:(2). Обозначимикак частичные суммы рядов (1) и (2). Рассмотрим суммучленов ряда (2):=. Поэтому;;т.е..

Итак, сумма ряда после перестановки уменьшилась вдвое. Это говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых.