Часть II. Колебания и волны

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА КОЛЕБАНИЙ МАЯТНИКА

Цель работы: определить логарифмический декремент колебаний маятника при наличии разных сил сопротивления и построить графики изменения амплитуды колебаний со временем.

Приборы и принадлежности: маятник, кювета со шкалой, приспособление для пуска маятника, секундомер, емкость с водой.

Теоретическое введение

Колебаниями называются движения или процессы, повторяющиеся во времени. Простейшим видом колебательного движения является гармоническое колебание. Оно возникает в том случае, когда на тело, выведенное из положения равновесия, действует сила F, направленная к положению равновесия и пропорциональная смещению:

F= –kx, (1)

где х– смещение тела от положения равновесия,k– коэффициент пропорциональности, который зависит от упругих свойств системы и называется коэффициентом квазиупругой силы. Знак минус показывает, что сила направлена противоположно смещению.

Второй закон Ньютона для материальной точки, совершающей гармоническое колебание, представляет собой дифференциальное уравнение второго порядка

, (2)

где m– масса материальной точки.

Решением уравнения (2) является выражение

x=Acos(t+), (3)

где A– амплитуда колебаний,– циклическая частота,– начальная фаза колебаний. Аргумент периодической функции

=t+(4)

называется фазой колебаний. При t= 0 фаза=. Начало отсчета можно выбрать так, чтобы= 0, тогда

x=Acost. (5)

График зависимости смещения хот времениtпредставляет собой график гармонического колебания (рис. 1).

Если колебания совершаются при наличии сил сопротивления, то энергия системы частично затрачивается на их преодоление. Вследствие этого амплитуда колебаний постепенно уменьшается, т.е. колебания будут затухающими.

Таким образом, затухающие колебания совершаются при наличии двух сил: силы, возвращающей систему в положение равновесия, и силы сопротивления среды. При малых скоростях сила сопротивления прямо пропорциональна скоростиυ:

F_сопр= –rυ, (6)

где r– коэффициент сопротивления среды. Знак минус показывает, что сила сопротивления направлена в сторону, противоположную скорости.

Для затухающих колебаний второй закон Ньютона имеет вид:

. (7)

Решением уравнения (7) является выражение:

x = A₀e^–tcos(t + α), (8)

где A₀ – начальная амплитуда колебаний; – коэффициент затухания, равный

 = ; (9)

 – циклическая частота затухающих колебаний, равная  = ;₀ – собственная частота колебаний системы. Собственной частотой колебаний называется частота колебаний в отсутствие сил сопротивления среды. Смещение колеблющейся системы в начальный момент времени равно x₀ = A₀cosα.

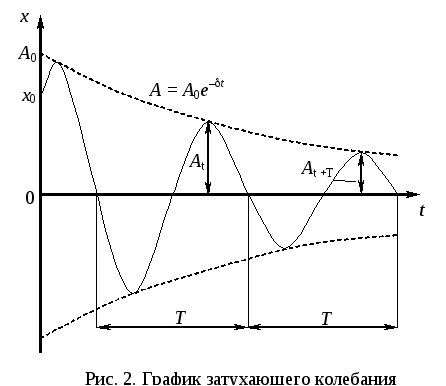
Из уравнения (8) видно, что амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону:

A = A₀e^–t. (10)

График затухающего колебания представлен на рис. 2.

Кроме перечисленных выше величин A₀, , , затухающие колебания характеризуются также логарифмическим декрементом D. Логарифмический декремент колебаний – безразмерная величина, равная натуральному логарифму отношения двух амплитуд, отстоящих друг от друга на время, равное одному периоду

D = 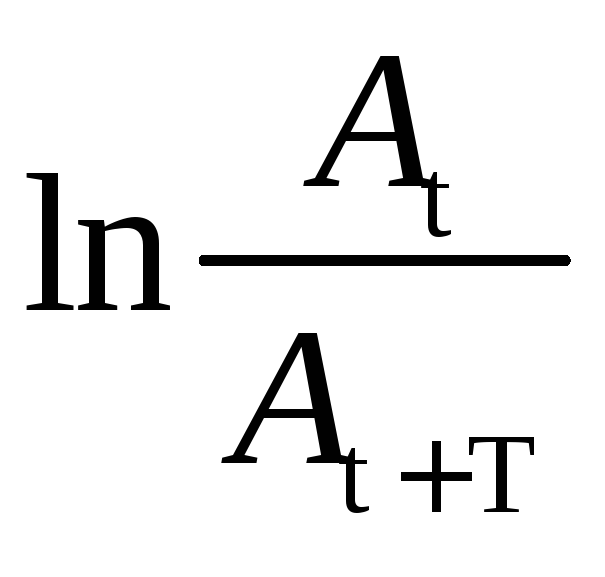(11)

Из формулы (11) следует, что логарифмический декремент – величина, обратная числу колебаний N_e, за которое амплитуда уменьшается в е раз. Для характеристики колебательной системы также используется величина, называемая добротностью Q. При малых значениях логарифмического декремента (D << 1) добротность колебательной системы равна Q ,

тогда

Q = N_e.

Подставив в уравнение (11) A_t = A₀e^–t и A_{t + T} = A₀e^{–(t + T)}, получим связь между параметрами затухающего колебания – логарифмическим декрементом, коэффициентом затухания и периодом колебаний:

D = Т. (12)

Для определения логарифмического декремента нужно измерить амплитуды двух последовательных колебаний и взять натуральный логарифм их отношения. На опыте измеряют амплитуду в начальный момент времени A₀и амплитуду A_tчерезNполных колебаний.

Получим формулу для вычисления логарифмического декремента. Выразим отношение двух амплитуд:

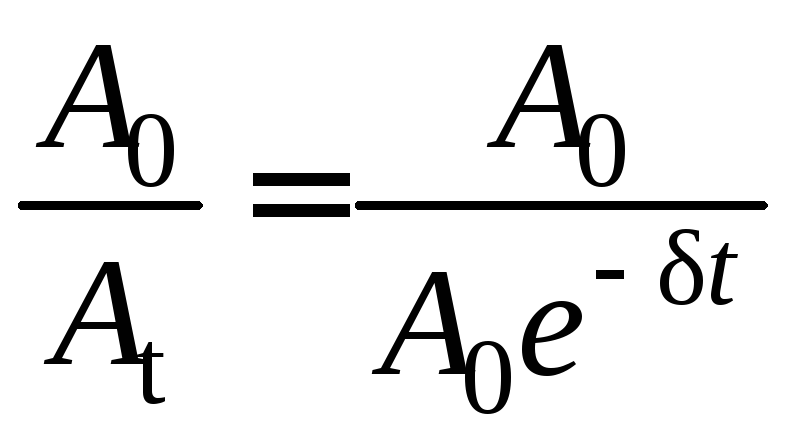=e^δt.

Так как t=NT, гдеN– число полных колебаний,Т– период колебаний, тоe^δNT.

Используя соотношение (12), получим

e^DN.

Найдем натуральный логарифм отношения амплитуд:

ln=lne^DN=DN,

откуда

D = . (13)

Описание установки

На рис. 3 изображена установка для наблюдения затухающих колебаний. Массивный маятник с длиной стержня около двух метров подвешен на треугольном стальном ноже 1, опирающемся на кронштейн 2. На стержне укреплен массивный диск 3. На нижнем конце стержня укреплен указатель 4 для отсчета числа делений по шкале 5. На стержне также закреплена лопатка 6. Маятник удерживается в отклоненном положении с помощью механического фиксатора 7. При повороте фиксатора маятник приходит в колебательное движение.

В работе изучаются затухающие колебания в воздухе и в воде. Чтобы заполнить кювету 8 водой, емкость 9 фиксируется в верхнем положении на кронштейне 10, и вода самотеком наливается в кювету через шланг.