
- •Оглавление
- •§1. Неопределенный интеграл
- •1.1. Основные понятия неопределенного интеграла
- •1.2. Основные методы интегрирования Метод непосредственного интегрирования
- •Замена переменной
- •Интегрирование по частям
- •1.3. Интегрирование рациональных дробей
- •1.4. Интегрирование тригонометрических функций
- •1.5. Интегрирование иррациональных функций
- •1.6. Примеры интегралов, не выражающихся через элементарные функции
- •1.7. Задания для самопроверки №1
- •§2. Определенный интеграл
- •2.1. Основные понятия и методы решения определенного интеграла
- •1. Непосредственное интегрирование.
- •2.2. Приближенное вычисление определенного интеграла
- •Формула прямоугольников
- •. Формула трапеций
- •Формула парабол (формула Симпсона или квадратурная формула)
- •2.3. Несобственные интегралы
- •1. Несобственные интегралы первого рода
- •2. Несобственные интегралы второго рода (интеграл от разрывной функции)
- •2.4. Задания для самопроверки №2
- •2.5. Геометрические приложения определенного интеграла
- •2.6. Физические приложения определенного интеграла
- •2.7. Экономическое приложение определенного интеграла
- •2.8. Химические приложения определенного интеграла
- •2.9. Задания для самопроверки №3
- •2.10. Вопросы и предложения для самопроверки Неопределенный интеграл
- •Определенный интеграл
- •Применение определенного интеграла
- •Расчётно-графическая работа
- •Графики некоторых функций, заданных параметрически и в полярных координатах
- •Структура интегрального исчисления
§1. Неопределенный интеграл
1.1. Основные понятия неопределенного интеграла
Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x) + C.
Записывается это
так:
![]()
Первообразной
функцией
для функции
f(x)
на промежутке (a;
b)
называется такая функция F(x),
производная которой равна f(x)
на рассматриваемом промежутке, то есть
![]() .
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Имеет место теорема: Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на некоторое постоянное слагаемое.
Функция f(x)
называется непрерывной
на отрезке [a,
b],
если 1) она
определена на этом множестве; 2) непрерывна
в каждой точке этого отрезка, то есть
![]() справедливо равенство
справедливо равенство![]() ,
где
,
где![]() .
.
Теорема (условие существования неопределенного интеграла). Всякая непрерывная на отрезке [a, b] функция имеет на этом промежутке неопределенный интеграл.
Основные теоремы (свойства неопределенного интеграла):
 где
C-const.
где
C-const. .
. .
.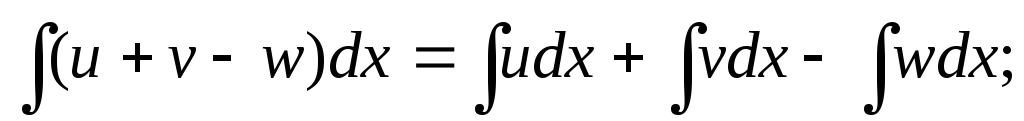 где u,
v,
w
– некоторые функции от х.
где u,
v,
w
– некоторые функции от х.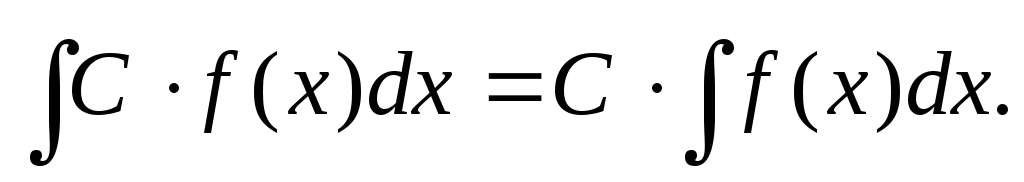
(Инвариантность формулы интегрирования). Если
 ,
то и
,
то и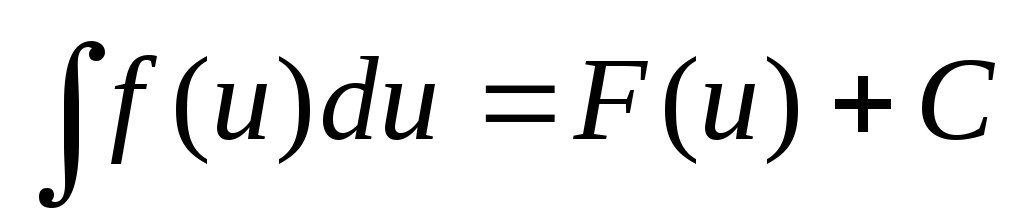 ,
где
,
где -
произвольная функция, имеющая непрерывную
производную.
-
произвольная функция, имеющая непрерывную
производную.
Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием.
Таблица 1.
|
Интеграл |
Значение |
Интеграл |
Значение | ||
|
1 |
|
|
11 |
|
|
|
2 |
|
|
12 |
|
|
|
3 |
|
|
13 |
|
|
|
4 |
|
|
14 |
|
|
|
5 |
|
|
15 |
|
|
|
6 |
|
|
16 |
|
|
|
7 |
|
|
17 |
|
|
|
8 |
|
|
18 |
|
|
|
9 |
|
|
19 |
|
|
|
10 |
|
|
20 |
|
|
1.2. Основные методы интегрирования Метод непосредственного интегрирования
Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Примеры:
a)
![]()
b)
![]()
![]()
с)
![]() .
.
Замена переменной
Этот метод
интегрирования основан на введении
новой переменной интегрирования.
Приведем пример: пусть дана сложная
функция f(x),
где
![]() - функция имеющая непрерывную производную
- функция имеющая непрерывную производную![]() .
Применяется свойство инвариантности
формулы интегрирования неопределенного
интеграла, получаем:
.
Применяется свойство инвариантности
формулы интегрирования неопределенного
интеграла, получаем:
![]() .
.
Эта формула называется формулой замены переменной в неопределенном интеграле.
Примеры:
a)

b)

![]()
![]() .
.
с)![]() .
.
Первый вариант
замены:
![]() =
= =
=![]()
Второй вариант замены:
![]() =
= =
=![]()
d)
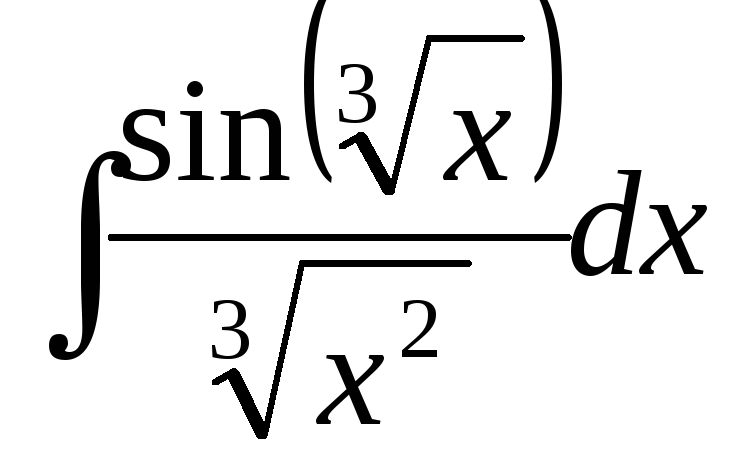 .
Первый вариант замены:
.
Первый вариант замены:
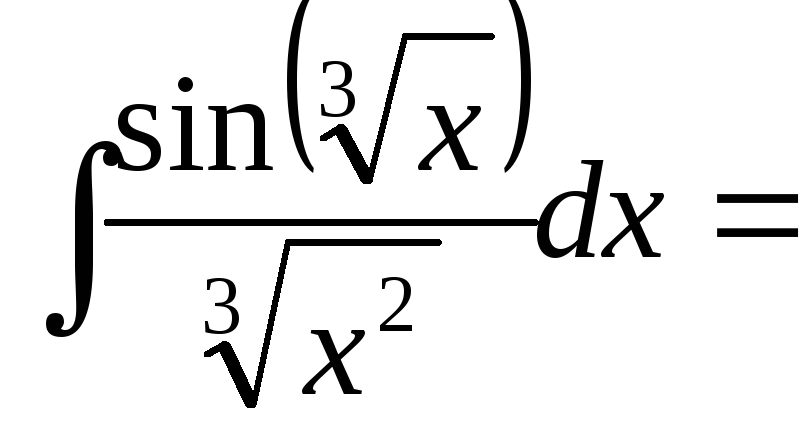
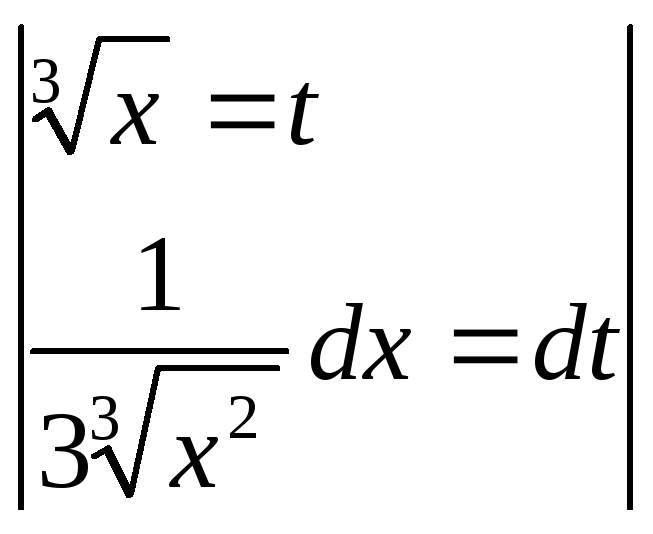 =
=![]()
Второй вариант
замены:
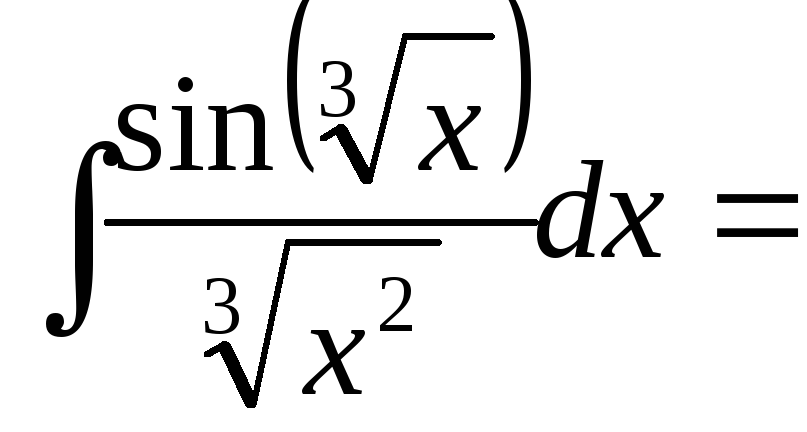
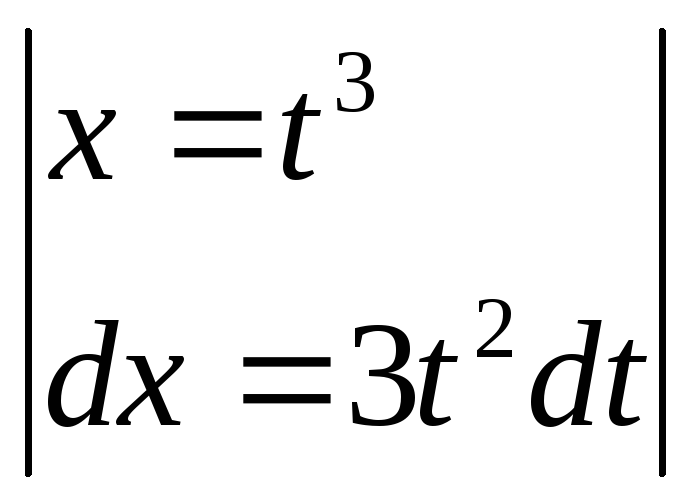 =
=![]()
=![]() .
.
При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах 3 – 7).
