Text_kursovoy_raboty (1)

Министерство образования и науки Российской Федерации

КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени

А. Н. ТУПОЛЕВА - КАИ

Кафедра автоматики и управления

Пояснительная записка к курсовой работе

по дисциплине «Информационные технологии»

на тему

Колебания маятника

Выполнила студентка группы 3139______________ Иванов А. С.

(подпись) (Фамилия И.О.)

Руководитель _______________ ______________

(должность, подпись) (Фамилия И.О.)

Оценка ____________

___________ ______________

(подпись) (Фамилия И.О.)

Казань, 2014

Оглавление

dt 9

#include <vc1. h> 9

#include "math.h" 10

4.1 назначение программы 0

ВВедение

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования

1. Постановка задачи

Дано: математический маятник. Требуется смоделировать колебания маятника с помощью языка С++

2МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Нам требуется получить уравнения движения данной системы. Воспользу-

емся для этого уравнением Лагранжа 2-го рода[1]:

Запишем выражение для кинетической энергии 1-го маятника:

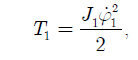
где . Выражение для кинетической энергии маятника (воспользовавшись теоремой о кинетической энергии тела при плоскопараллельном движении):

Выражение для потенциальной энергии маятника:

Итого, выражения для потенциальной

Подставив выражения для кинетической (2.6) и потенциальной (2.7) энер-

гий системы в уравнения Лагранжа (2.1), получим уравнения движения системы:

Полученная система (2.8) представляет собой систему двух связанных

обыкновенных нелинейных дифференциальных уравнения 2-го порядка отно-

сительно неизвестных 1ϕ (t) и 2ϕ (t).

Постановку задачи также необходимо дополнить начальными условиями:

1 Кинетическая энергия тела при его плоскопараллельном движении равна сумме тех кинетических энергий,

которые имело бы данное тело при его поступательном движении со скоростью центра масс тела и при его

вращательном движении вокруг оси, проходящей через центр масс тела и перпендикулярной к той непод-

вижной плоскости, параллельно которой движется тело[2].

Также, представляет интерес рассмотреть малые колебания системы без

трения. Получить уравнения движения в этом случае можно из системы (2.8)

положив равными 0 все нелинейные члены, косинус малого угла равным 1, а

синус малого угла равным самому углу. Тогда получим уравнения малых

колебаний данной системы (запишем их в матричной форме):

которые также следует дополнить начальными условиями (2.9).

В результате выполнения работы, мы должны:

1) решить поставленную задачу в линейной постановке, определить

собственные частоты и формы колебаний системы;

2) решить численно поставленную задачу в общей постановке без трения,

получить анимацию процесса колебаний;

3) смоделировать процесс колебаний без трения используя CAD/CAE сис-

темы, получить анимацию;

4) подобрать параметры системы так, чтобы более ярко выразить ее хаоти-

ческое поведение.

3 МЕТОДИКА РЕШЕНИЯ ЗАДАЧИ

3.1 Задача о малых колебаниях

Сначала решим задачу о малых колебаниях (2.9),(2.10), как самую простую

и имеющую аналитическое решение. В результате решения, мы должны полу-

чить собственные частоты и формы системы, а также зависимости ϕ1(t) и 2ϕ (t).

Введем обозначения:

Тогда уравнение движения запишется в виде:

где U, P,θ – некоторые константы, подлежащие отысканию. Подставим решение (3.3) в уравнение (3.2). После приведения получим:

Эта система имеет решения только если Запишем это условие в развернутом виде:

Раскрыв определитель, получаем биквадратное уравнение относительно P :

Обозначив

получим

Выражение (3.8) представляет собой значение первой и второй собствен-

ных частот системы. Подставим каждую из полученных собственных частот (3.8)

в уравнение форм колебаний (3.4):

Отсюда получаем собственные формы колебаний с точностью до постоянного множителя:

Решение задачи возьмем в виде разложения по собственным формам:

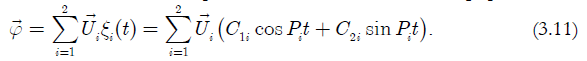
Неопределенные константы 11 12 21 22 C₁₁ ,C₁₂ ,C₂₁ ,C₂₂ находим из начальных условий (2.9)

Таким образом, задача о малых колебаниях решена.

МОДЕЛВРОВАНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ НA ПРИMEPE МАТЕМАТИЧЕСКОГО МАЯТНИКА В СРЕДЕ С++ BUILDER

Основой физического образования является физический эксперимент и фундаментальная теория. После освоения техники и методов реального физического экспериментирования в учебных лабораториях (практические действия с материальными обьектами, измерительными приборами и т.д.) студенты физико — математических факультетов ( а также многих технических) могут перейти к исследованию компьютерных (виртуальных) моделей физических явлений, эффектов и процессов взаимодействия, развивая свое предметно - образное мышление и осваивая методы исследовательской деятельности.

Если тело совершает свободные незатухающие колебания, то его координата с течением времени изменяется по закону косинуса или синуса

где — амплитуда фаза колебаний, — начальная фаза, —собственная циклическая (круговая) частота колебаний. Скорость (первая производная координаты по времени) и ускорение (вторая производная координаты повремени) при этом также будут изменяться по гармоническому закону:

dt

а

Для преобразования выражений мы воспользовались формулами приведения. Отсюда видно, что скорость опережает смещение по фазе на а ускорение - на т, т.е. находится в противофазе со смещением. Одной из самых простых и распространенных моделей колебательных систем является математический маятник: материальная точка массы т, подвешенная на нерастяжимой нити длиной и совершающая колебания в вертикальной плоскости. Круговая частота колебаний в этом случае принимается равной

Цель настоящей работы заключается в том, чтобы построить графики зависимости х(/), v(/), а(/) и проследить за их изменением при изменении параметров системы в среде C++Builder.

Загрузка файла.

1. Запустить C++Builder..

2.Открыть шаблон Форма 1 Свободные колебания математического маятника. cpp.

Очевидно, исходными данными являются. 1) амплитуда (максимальное смещение)

2) начальная фаза ‹р , 3) длина нити Z,4) временной интервал. Постоянные величины. амплитуда, начальная фаза, длина нити, период (частота) колебаний. Переменные — смещение тела в каждый момент времени (координата х), скорость и время.

Программа в среде С++ Builder:

Список литературы:

1. Стародубцев В.А. Использование информационных технологии на лекциях по естественнонаучным дисциплинам. Информатика и образование. 2003.

2. Кравченко Н.С., Ревинская О.Г. Изучение основных законов механики с помощью моделирующих лабораторных работ на компьютере. Материалы XV Международной конференции «Применение новых технологии в образовании». Троицк. Тровант, 2004.

текст программы

#include <vc1. h>

#pragma hdrstop

#include "Unit 1.h"

#include "math.h"

#pragma package(smart_init)

#pragma resource "*.dfm" TForm l *Form l ; Graphics..TBitmap *bgp,

fastcall TForm I::TForm I(TComponent* Owner) TForm(Owner)

bgp=new Graphics:: TBitmap_0:

bgp->LoadFromFile("sky. bmp"); catch(EFOpenError &e)

void fastcall TForml::FormPaint(TObject *Sender)

Canvas—>Draw(0,0,bgp); Canvas—>Bmsh->Style=bsClear;

void fastcall TForml::FormResize(TObject *Sender)

Form I ->Refresh();

void fastcall TForml::Button1Click(TObject *Sender)

double t,x,v,a,xmax=0.3,tmax=l 0.0;

double L=l,p=3. 14159265358979;

double g=9.80665,w=sqrt( L),T=2*p/w,f=p/6; ro o;

while (t< max)

x max*sin(w*t+I);

*xmax*cos(w*t+I); a=—w*w*xmax*sin(w*t+I ); Senesl ->AddXY(t,x,"",clBlue); Series2->AddXY(t,v,"",clGreen); Series3—>AddXY(t,a,"",c1Red);

4.1 назначение программы

Программа предназначена для моделирования колебания маятника

4.2. Исходные параметры программы

1)амплитуда (максимальное смещение) х_max

2)начальная фаза φ

3)длинна нити L

4)Временной интервал

4.5 Выходные данные

1)Период Т

2)Скорость ν

3)Ускорение а