
- •Краткий конспект лекций по теории вероятностей Лекция1 Вероятность
- •Действия над событиями.
- •Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.
- •Полная группа событий – это совокупность n событий а1, а2, …, Аn, одно из которых обязательно произойдет, т.Е. Свойства операций над событиями
- •Правило двойственности (теорема де Моргана)
- •Алгебра событий.
- •Вероятность. Классическое определение вероятности события
- •Геометрическая вероятность
- •Статистическая вероятность
- •Свойства вероятности
- •Лекция 2 Условная вероятность.
- •Формула вероятности произведения событий (теорема умножения вероятностей). Независимые события
- •Формула вероятности суммы совместных событий (теорема сложения вероятностей)
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Лекция 3. Случайные величины
- •Лекция 4 Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Лекция 5
- •Лекция 6. Двумерные случайные величины
- •Свойства функции распределения.
- •Свойства плотности.
- •Свойства коэффициента корреляции.
- •Двумерное равномерное распределение
- •Двумерное нормальное распределение
- •Задача линейного прогноза.
- •Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
- •Законы больших чисел.
- •Теорема Чебышева
- •Обобщенная теорема Чебышева.
- •Теорема Маркова.
- •Теорема Бернулли.
- •Предельные теоремы.
- •Теорема Ляпунова.
- •Теорема Леви – Линдеберга.
- •Интегральная теорема Муавра – Лапласа.
- •Лекция 8 Элементы математической статистики
- •Основные задачи статистики.
- •Эмпирические законы распределения.
- •Точечные оценки параметров распределения.
- •Требования к оценкам.
- •2. Несмещенная, состоятельная оценка дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
- •Доверительный интервал для среднеквадратического отклонения .
Лекция 3. Случайные величины
Случайная величина – это величина (число), которая в результате опыта может принимать то или иное значение.
Более строго,
случайная величина – это числовая
функция случайного события.
![]()
Случайная
величина называется дискретной,
если множество ее значений конечно или
счетно. Здесь![]() -
алгебра событий. Например, число очков
на грани брошенной кости, число бросков
монеты до появления герба – дискретные
случайные величины.
-
алгебра событий. Например, число очков
на грани брошенной кости, число бросков
монеты до появления герба – дискретные
случайные величины.
Случайная
величина называется непрерывной,если ее значения заполняют некоторый
интервал, возможно, бесконечный. Здесь![]() -
сигма - алгебра событий. Например,
расстояние от центра мишени при стрельбе,
время до отказа прибора, ошибка измерения
– непрерывные случайные величины.
-
сигма - алгебра событий. Например,
расстояние от центра мишени при стрельбе,
время до отказа прибора, ошибка измерения
– непрерывные случайные величины.
Рассмотрим
дискретную случайную величину,
принимающую значения![]() .
Имеем полную группу (иначе, не все
значения учтены) несовместных событий
.
Имеем полную группу (иначе, не все
значения учтены) несовместных событий![]() .
Вероятности этих событий равны
соответственно
.
Вероятности этих событий равны
соответственно![]()
![]() .
Будем говорить, что дискретная случайная
величина
.
Будем говорить, что дискретная случайная
величина![]() принимает значения
принимает значения![]() с вероятностями
с вероятностями![]() .
.
Законом
распределения дискретной случайной
величины называется любое соотношение,
устанавливающее зависимость между ее
значениями![]() и вероятностями
и вероятностями![]() ,
с которыми эти значения достигаются.
,
с которыми эти значения достигаются.
Основные формы закона распределения дискретной случайной величины: ряд распределения– таблица
-
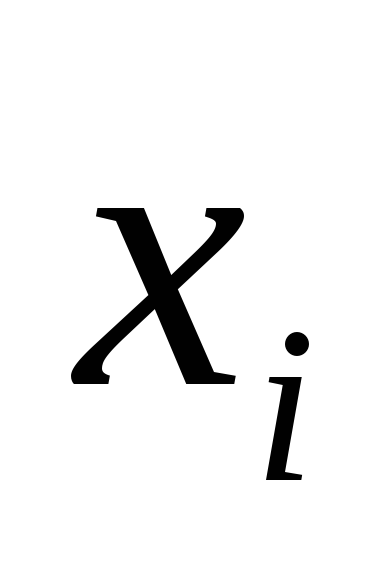
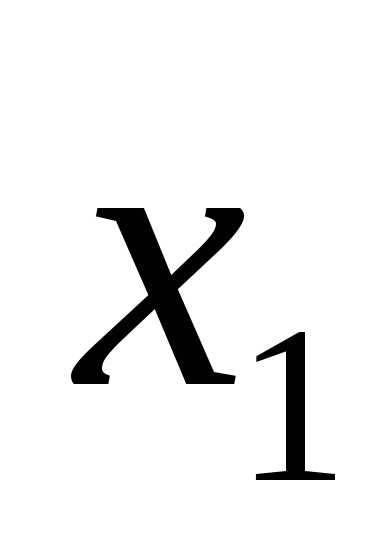
…..
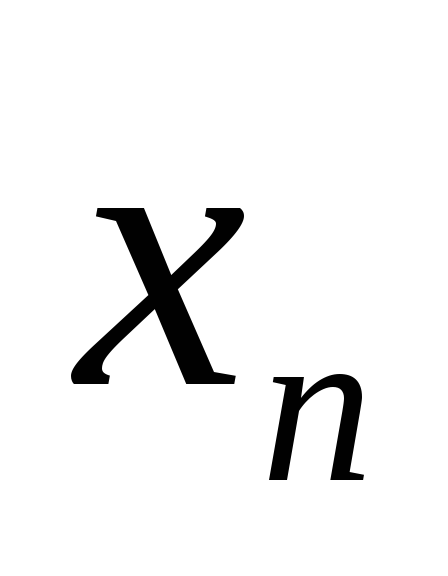
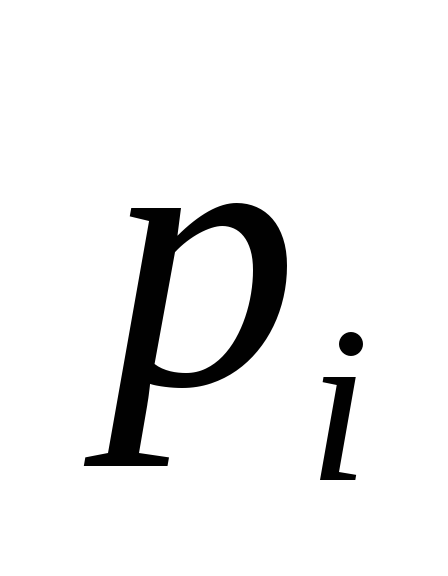
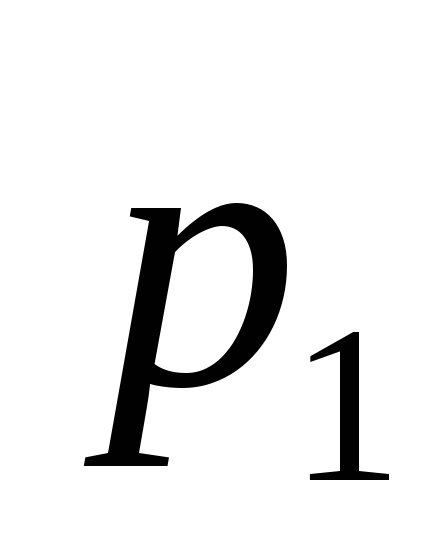
…..
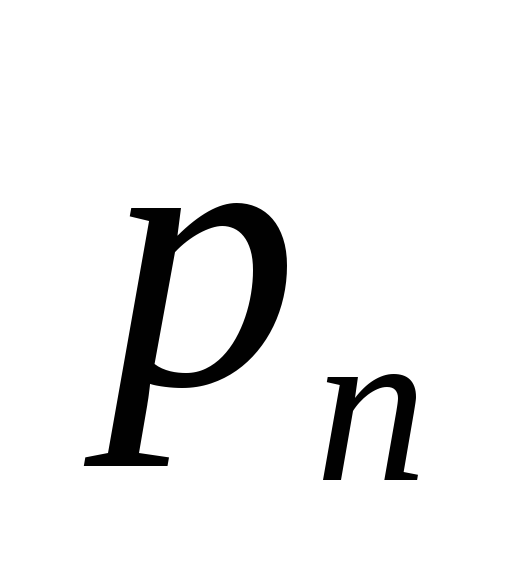
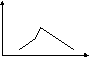
многоугольник
распределения
p3
p2
p1,pn
x1 x2 x3 …xn
Можно задать
закон распределения в виде аналитической
зависимости, связывающей значения![]() и вероятности
и вероятности![]() .
.
Рассмотрим
непрерывную случайную величину.Для непрерывной случайной величины![]() ,
поэтому рассматривают события
,
поэтому рассматривают события![]() и вероятности этих событий.
и вероятности этих событий.
Функцией
распределения непрерывной случайной
величины ![]() называется вероятность события
называется вероятность события![]() .
.![]() =
=![]() .
.
Свойства функции распределения.

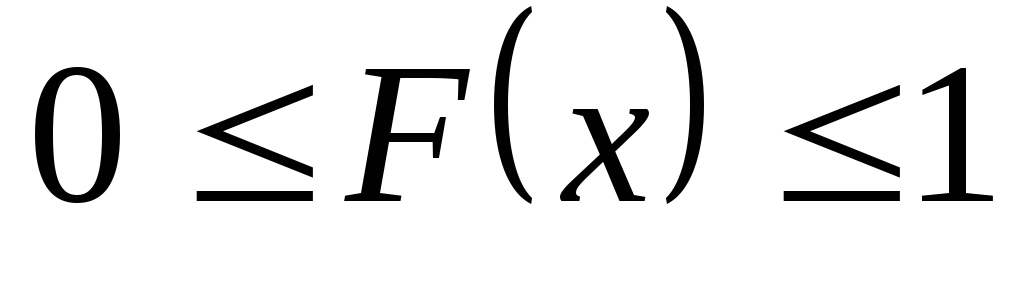 по аксиомам вероятности,
по аксиомам вероятности,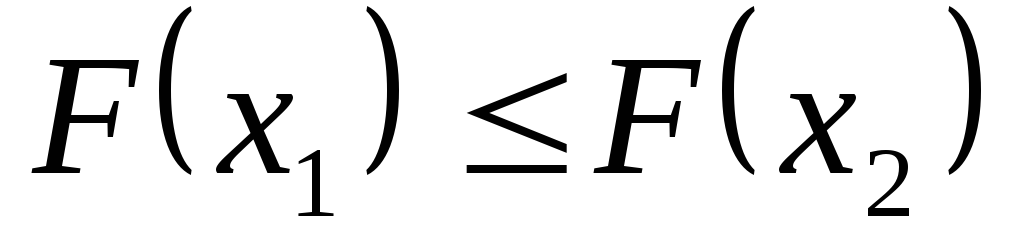 ,
если
,
если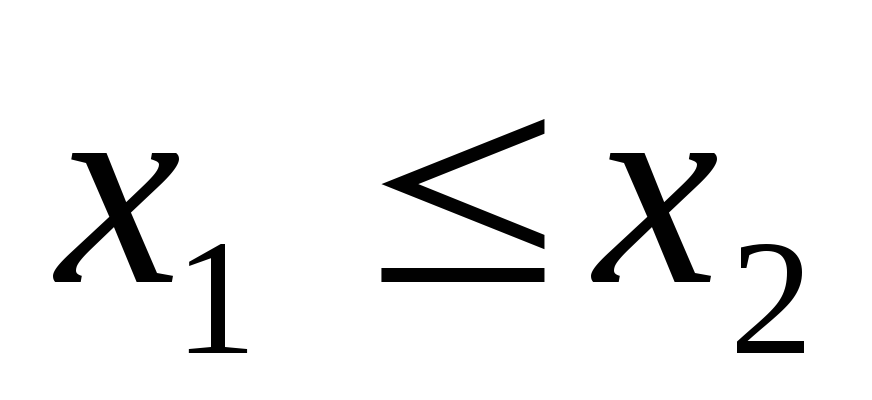 ,
т.е.функция распределения – неубывающая
функция. В самом деле,
,
т.е.функция распределения – неубывающая
функция. В самом деле, ,
следовательно,
,
следовательно,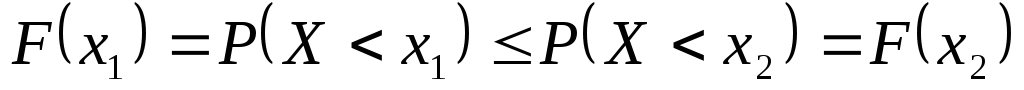 .
.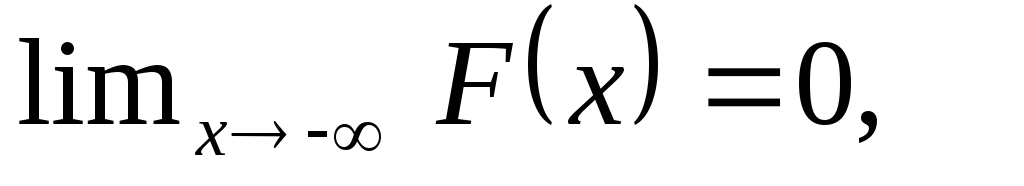
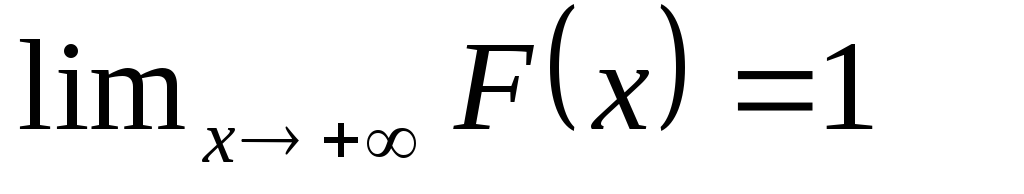 В
самом деле, событие
В
самом деле, событие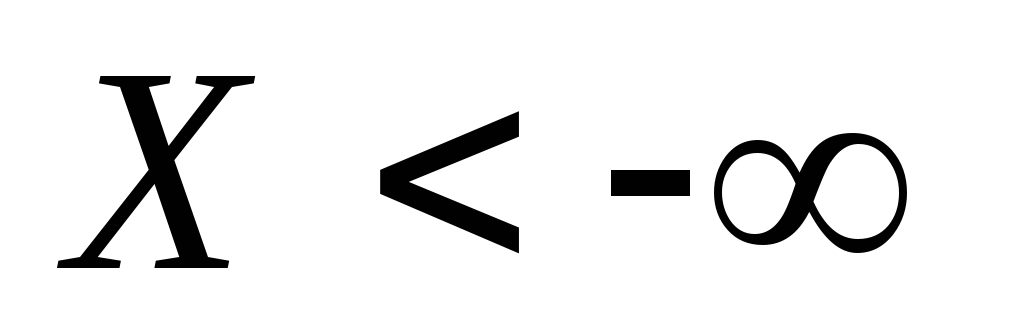 - невозможное, и его вероятность нулевая.
Событие
- невозможное, и его вероятность нулевая.
Событие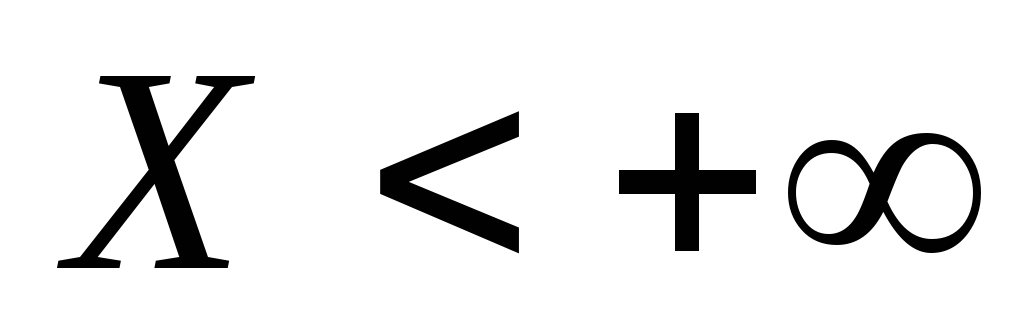 - достоверное, и его вероятность равна
1.
- достоверное, и его вероятность равна
1.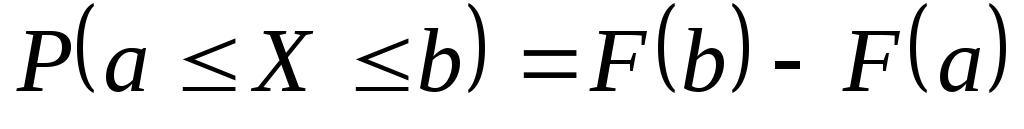 .
Так как события
.
Так как события несовместны и событие
несовместны и событие есть сумма этих событий, то
есть сумма этих событий, то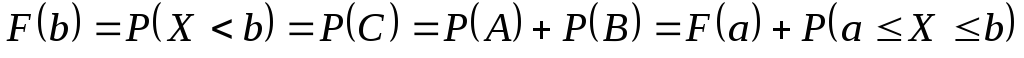 .
.
График функции распределения имеет, примерно, следующий вид
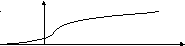 F(x)
F(x)
 1
1
x
Функцию распределения можно определить и для дискретной случайной величины. Ее график будет графиком ступенчатой функции со скачками в piв точкахxi, непрерывной слева в этих точках.
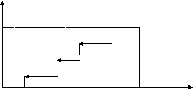 F(x)
F(x)
 1
1
p3
 p2
p2
p1
x
x1 x2 x3 xn
Для непрерывной случайной величины вводится плотность распределения вероятностей.
Плотностью
распределения (вероятностей) называется
производная функции распределения![]() .
.
Ясно, что
![]() .
.
Часто функцию
распределения называют интегральным
законом распределения, а плотность
распределения – дифференциальным
законом распределения.Так как![]() ,
тоp(x)dxназываетсяэлементом вероятности.
,
тоp(x)dxназываетсяэлементом вероятности.
Свойства плотности распределения.
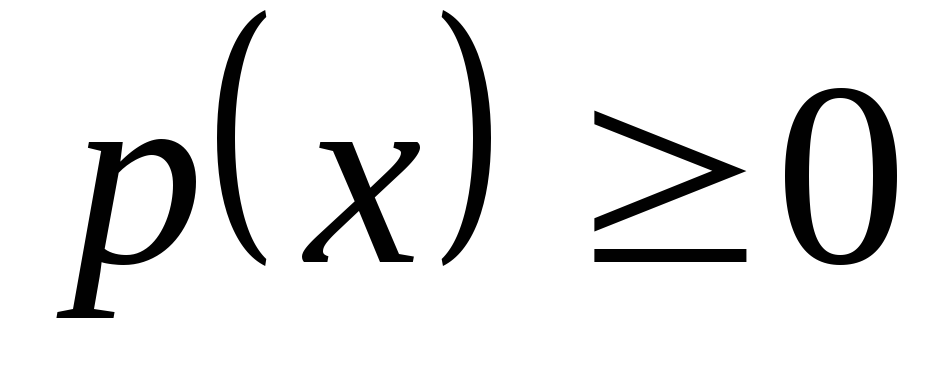 ,
так как функция распределения –
неубывающая функция,
,
так как функция распределения –
неубывающая функция,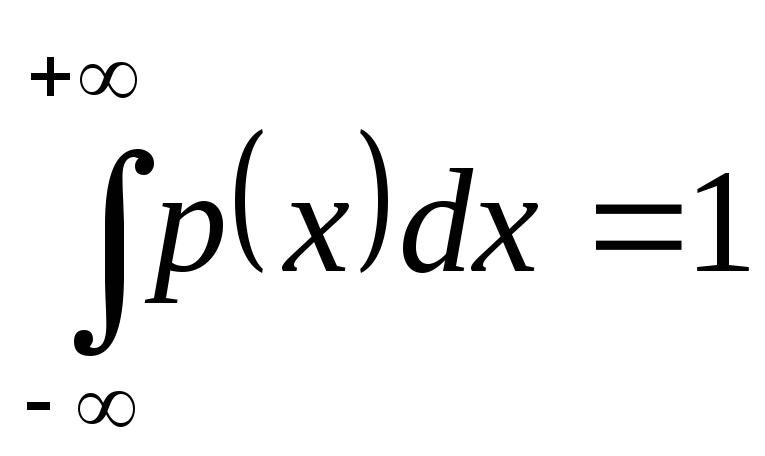 (условие нормировки), так как
(условие нормировки), так как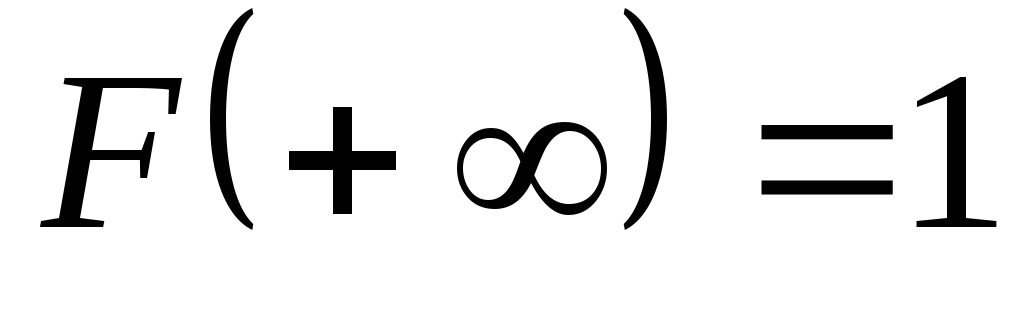 .
.
Числовые характеристики случайных величин.
Начальный момент s-го порядка
Для дискретных
случайных величин
![]() .
.
Для непрерывных
случайных величин
![]() .
.
Математическим
ожиданием случайной величины
называется ее первый начальный моментmx=M(x) =
![]() .
.
Для дискретных
случайных величин
![]() .
Если на числовой оси расположить точки
.
Если на числовой оси расположить точки![]() с массами
с массами![]() ,
то
,
то![]() -
абсцисса центра тяжести системы точек.
Аналогично, для непрерывных случайных
величин
-
абсцисса центра тяжести системы точек.
Аналогично, для непрерывных случайных
величин![]()
![]() имеет смысл центра тяжести кривой
распределения.
имеет смысл центра тяжести кривой
распределения.
Свойства математического ожидания.
M (C ) = C.
Для дискретных случайных величин x=C,p= 1,M(C) =xp=С.
Для непрерывных случайных
величин
![]() по условию нормировки для плотности
вероятностей.
по условию нормировки для плотности
вероятностей.
M(CX) = СM(X). В самом деле, константу можно вынести из суммы в дискретном случае и из под интеграла в непрерывном случае.
M(X+Y) =M(X) +M(Y). (без доказательства).
M(|X|) = |M(X)| (без доказательства).
Математическое ожидание функции случайной величины вычисляют по формулам
![]() для дискретной случайной величины,
для дискретной случайной величины,
![]() для непрерывной случайной величины.
для непрерывной случайной величины.
Центрированной
случайной величиной называется![]() .
.
Центральный момент s-го порядка
Для дискретной
случайной величины
![]() .
.
Для непрерывной
случайной величины
![]() .
.![]()
Дисперсией
называется второй центральный момент
случайной величины.![]()
По свойствам
математического ожидания получим
![]() .Эта формула часто применяется.
Дисперсия – это характеристика рассеяния,
она характеризует концентрацию кривой
распределения (графика плотности
распределения) около математического
ожидания. Если на числовой оси расположить
точкиxiс массамиpi,
то дисперсия – это момент инерции
системы материальных точек относительно
центра тяжестиmx.
.Эта формула часто применяется.
Дисперсия – это характеристика рассеяния,
она характеризует концентрацию кривой
распределения (графика плотности
распределения) около математического
ожидания. Если на числовой оси расположить
точкиxiс массамиpi,
то дисперсия – это момент инерции
системы материальных точек относительно
центра тяжестиmx.
Для дискретных
случайных величин
![]() .
.
Для непрерывных
случайных величин
![]() .
.
Свойства дисперсии.
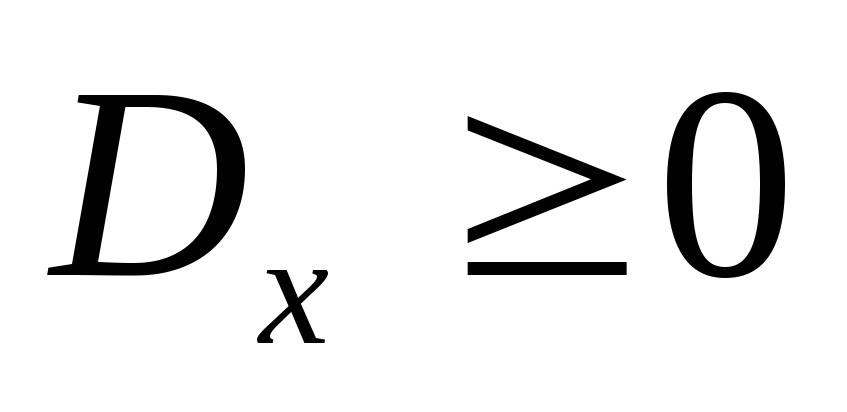 (под интегралом стоит квадрат функции).
(под интегралом стоит квадрат функции).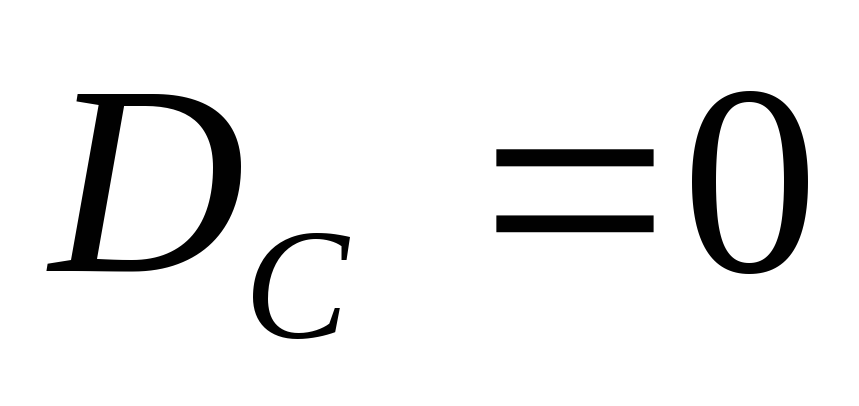 (
(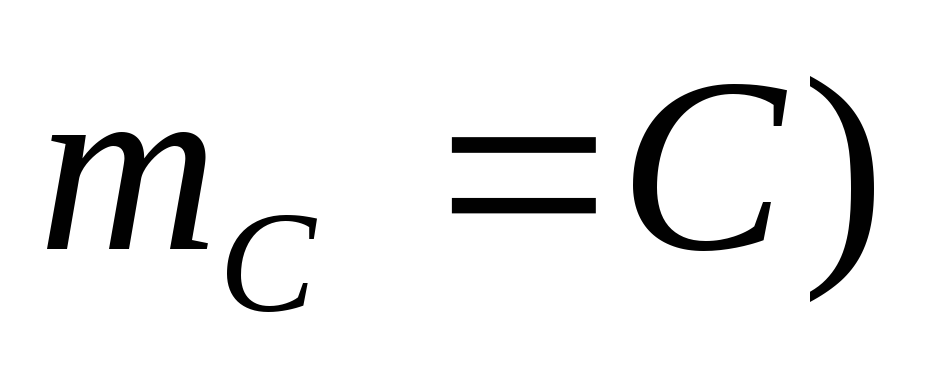 .
.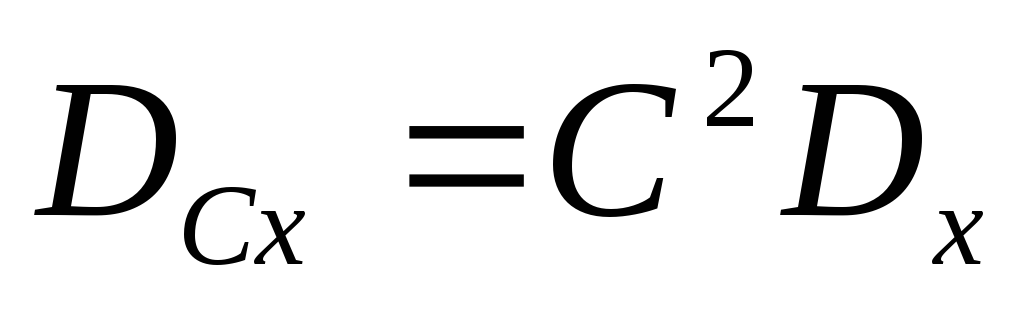 (выведите сами, вынося
(выведите сами, вынося из под суммы или из под интеграла).
из под суммы или из под интеграла).
Средним
квадратическим отклонениемназывается![]() .
.
Кроме этих
основных числовых характеристик
используются коэффициент асимметрии
![]() ,эксцесс –мера островершинности
распределения
,эксцесс –мера островершинности
распределения![]() ,среднее арифметическое отклонение
,среднее арифметическое отклонение
![]() ,мода– наиболее вероятное значение
для дискретных величин или значение,
где плотность максимальна для непрерывных
величин,медианаMe–
абсцисса точки, в которой площадь,
ограниченная кривой плотности
распределения, делится пополам (точка,
в которойF(x)
= ½).
,мода– наиболее вероятное значение
для дискретных величин или значение,
где плотность максимальна для непрерывных
величин,медианаMe–
абсцисса точки, в которой площадь,
ограниченная кривой плотности
распределения, делится пополам (точка,
в которойF(x)
= ½).
Пример. Стрелок делает один выстрел и с вероятностьюpпопадает в мишень. ПустьX– количество попаданий в мишень. Это – дискретная случайная величина, принимающая два значения х1= 0 и х2= 1 с вероятностями q = 1-p,pсоответственно. Построим ряд распределения Х
-
xi
0
1
pi
q
p
Функция
распределения равна
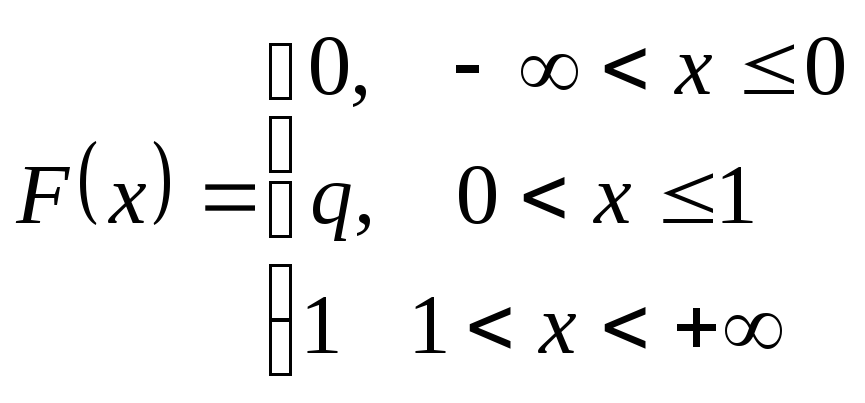 ,
,
Математическое ожидание равно M(X) =mx= 0q+ 1p=p.
Если составить ряд распределения для случайной величины X2, то мы получим ту же таблицу (так как 02= 0 и 12=1). ПоэтомуM(X2) =p, а дисперсию можно вычислить по формулеD(X) =M(X2) – (mx)2=p–p2=p(1-p) =pq.
Распределение называется равномерным на отрезке [a,b], если плотность случайной величиныXпостоянна на отрезке [a,b]p(x) =pи равна нулю вне этого отрезка.
Из условия нормировки для плотности вероятности следует
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() -плотность равномерного распределения.Функция распределения величины,
распределенной равномернона отрезке
[a,b],равна
-плотность равномерного распределения.Функция распределения величины,
распределенной равномернона отрезке
[a,b],равна
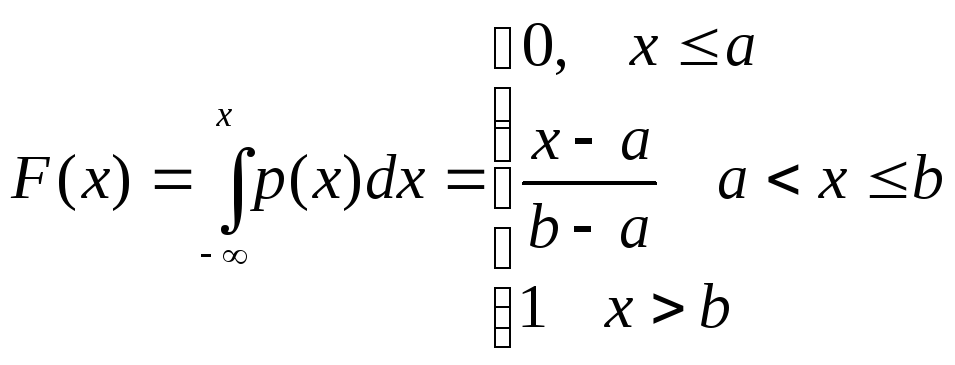 .
Вычислим математическое ожидание и
дисперсию величины, распределенной
равномерно на отрезке [a,b].
.
Вычислим математическое ожидание и
дисперсию величины, распределенной
равномерно на отрезке [a,b].
![]() ,
,
![]() =
=
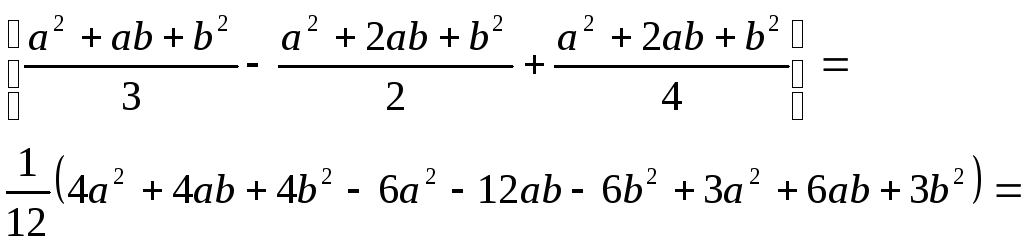
=![]()
