5.2. Методы решения многокритериальной задачи оптимизации

Метод обобщенного критерия. Метод перехода от несколь-

ких критериев f1,f2,…fm к одному, задаваемому новой функцией

m

z = ∑(α j f j )

j=1

рия. Числа

называется сверткой или методом обобщенного крите-

α j называются весовыми коэффициентами. Чем больше

α j , тем больший «вклад» вносит j-й критерий в обобщенный крите-

m

рий z. Иногда требуют, чтобы ∑α j =1.

j=1

Пример 5.3. Решить задачу методом обобщенного критерия

f1		= 4x1 + x2			→ max
f	2	= x	+ 2x	2	→ max
		1
		+ x2	≤ 7
x1					.
x1		≤ 5
x	2	≤ 4
		≥ 0
x
	1
x2 ≥ 0
Решение. Пусть α1		= 0,4 , α2			= 0,6 . Тогда задача двухкритери-
альной оптимизации сводится					к задаче одного критерия

z =α1 f1 +α2 f2 = 0,4(4x1 + x2 ) + 0,6(x1 + 2x2 ) = 2,2x1 +1,6x2 → max

x1 + x2 + x3 = 7x1 + x4 = 5x2 + x5 = 4

xi ≥ 0, i =1,5

Перепишем целевую функцию z в виде z − 2,2x1 −1,6x2 = 0 . Составим начальную симплекс-таблицу

		Б.П.		с.ч.		х1	х2	х3 х4 х5
		х3	7		1		1	1	0	0
		х4	5		1		0	0	1	0
		х5	4		0		1	0	0	1
		z	0		-		-1,6	0	0	0
					2,2
Вводим в базис переменную x1 и, так как													7	;	5		= 5 , выво-
											min		1		1
дим из базиса x4.
		Б.П.		с.ч.		х1	х2	х3	х4	х5
																	72

	х3	2	0		1	1	-1	0
	х1	5	1		0	0	1	0
	х5	4	0		1	0	0	1
	z	11	0		-1,6	0	2,2	0
Вводим в базис переменную x2						и,	так как			2	;	4		= 2 , выво-
									min	1		1
дим из базиса x3.
	Б.П.	С.ч.		х1 х2		х3	х4	х5
	х2	2		0	1	1	-1	0
	х1	5		1	0	0	1	0
	х5	2		0	0	-1	1	1
	z	14,2		0	0	1,6	0,6	0

Последняя строка и столбец свободных членов содержит только положительные числа, следовательно, мы получили опти-

мальное решение	z*=14,2, X*=(5;2).	При этом f1*	= f1 (5;2) = 22 ,
f2* = f2 (5;2) = 9.
Замечание	5.2. Выбор весовых	коэффициентов	α j имеет

субъективный характер.

Метод приоритетов. Метод приоритетов решения много-

критериальных задач применяется в том случае, когда критерии fi

упорядочены по их относительной важности.

На первом шаге решения задачи отбирают множество исходов, которые имеют максимальную оценку по важнейшему критерию. Если исход единственный, то он и является оптимальным. Если же исходов несколько, то среди них выбирают те, которые имеют максимальную оценку по второму по важности критерию. Если опять исходов несколько, то процесс повторяют для следующих критерий.

Пример 5.4. Решить двухкритериальную задачу методом приоритетов.

f1		= 4x1 + x2			→ max
f	2	= x	+ 2x	2	→ max
		1
		+ x2	≤ 7
x1					.
x1		≤ 5
x	2	≤ 4
		≥ 0
x
	1	≥ 0
x2

Решение. Предположим, что критерий f1 предпочтительнее (приоритетнее) критерия f2 ( f1 f2 ).

1 шаг. Решим задачу

73

f1 = 4x1 + x2 → maxx1 + x2 ≤ 7

x1 ≤ 5

x2 ≤ 4x1 ≥ 0x ≥ 02

симплекс методом.

Приведем систему ограничений к каноническому виду

x1 + x2 + x3 = 7x1 + x4 = 5x2 + x5 = 4

xi ≥ 0, i =1,5

Запишем целевую функцию в виде f1 − 4x1 − x2 = 0. Начальная симплекс-таблица имеет вид:

	Б.П.	с.ч.		х1 х2 х3 х4 х5
	х3	7	1		1	1	0	0
	х4	5	1		0	0	1	0
	х5	4	0		1	0	0	1
	f1	0	-4		-1	0	0	0		7		5
Вводим в базис переменную x1						и,	так как				;			= 5 , выво-
									min	1		1
дим из базиса x4.
	Б.П.	с.ч.		х1 х2 х3 х4 х5
	х3	2	0		1	1	-1	0
	х1	5	1		0	0	1	0
	х5	4	0		1	0	0	1
	f1	20	0		-1	0	4	0		2		4
Вводим в базис переменную x2						и,	так как				;			= 2 , выво-
									min	1		1
дим из базиса x3.
	Б.П.	С.ч.		х1 х2 х3 х4 х5
	х2	2		0	1	1	-1	0
	х1	5		1	0	0	1	0
	х5	2		0	0	-1	1	1
	z	22		0	0	1	3	0

Так как столбец свободных членов и последняя строка содержат только положительные числа, то мы получим оптимальное ре-

шение X*=(5;2), f1max = f1 (5;2) = 22 . При этом f2 = 9 .

2 шаг. Решим задачу для второго по важности критерия

74

f2 = x1 + 2x2 → maxx1 + x2 ≤ 7

x1 ≤ 5x2 ≤ 4

4x1 + x2 ≥ 22

x1 ≥ 0x2 ≥ 0

Приведем систему ограничений к каноническому виду

x1 + x2 + x3 = 7x1 + x4 = 5x2 + x5 = 4

4x1 + x2 − x6 = 22

xi ≥ 0, i =1,6

и запишем целевую функцию в виде f2 − x1 − 2x2 = 0 Составим начальную симплекс таблицу

Б.П.	с.ч.	х1 х2 х3 х4 х5 x6
х3	7	1	1	1	0	0	0
х4	5	1	0	0	1	0	0
х5	4	0	1	0	0	1	0
x6	-22	-4 -1 0 0 0 1
f2	0	-1 -2 0			0	0	0

Так как столбец свободных членов содержит отрицательный элемент, то применим двойственный симплекс-метод.

Выводим из базиса х6 и вводим в базис х1.

Б.П.			с.ч.		х1				х2	х3 х4 х5				x6
х3			3/2			0			3/4	1	0	0		1/4
х4			-1/2			0			-1/4 0		1	0		1/4
х5			4			0			1	0	0	1		0
x1			11/2			1			1/4	0	0	0		-1/4
	f2		11/2			0			-7/4 0		0	0		-1/4
	Б.П.			с.ч.			х1 х2 х3 х4 х5 x6
	х3			0				0	0	1	3	0		1
	х2			2				0	1	0	-4	0	-1
	х5			2				0	0	0	4	1		1
	x1			5				1	0	0	1	0		0
	f2			9				0	0	0	-7 0 -2

Все элементы столбца свободных членов положительны, поэтому продолжим решение задачи симплекс-методом.

75

	Б.П.		с.ч.		х1 х2 х3 х4					х5	x6
	х3	-3/2			0	0	1	0		-3/4	1/4
	х2	4			0	1	0	0		1	0
	х4	1/2			0	0	0	1		1/4	1/4
	x1	9/2			1	0	0	0		-1/4	-1/4
	f2	25/2			0	0	0	0		7/4	-1/4
	Б.П.		с.ч.		х1 х2		х3		х4 х5		x6
	х5		2		0	0	-4/3		0	1	-1/3
	х2		2		0	1	4/3		0	0	1/3
	х4		0		0	0	1/3		1	0	1/3
	x1		5		1	0	-1/3		0	0	-1/3
	f2		9		0	0	7/3		0	0	1/3

Все элементы столбца свободных членов и последней строки положительны, следовательно, мы получили оптимальное решение

X*=(5;2), f2 = 9 .

Ответ. X*= (5;2), f*=(22;9).

Метод идеальной точки. Метод идеальной точки является «геометрическим» методом для многокритериальных задач. Продемонстрируем его на следующем примере:

Пример 5.5. (многокритериальная задача об использовании ресурсов). Для выпуска двух видов продукции используется два вида

ресурсов. Известны		1	3		– матрица норм расхода сырья,
	A =	2	2
Q = (2,1) – стоимость ресурсов,					P = (6,9) – цена реализации продук-

ции, B = 18 – запасы ресурсов. Найти план производства, максими-

16

зирующий одновременно выручку и прибыль (или, что эквивалентно, максимизирующий прибыль и минимизирующий затраты на ресурсы).

Решение.						x
	Если X =						1	– план производства, то стоимость
							x
							2
ресурсов QAX = 4x1 +8x2 ,							выручка		f1 = PX = 6x1 +9x2 ,		прибыль
f2 = PX −QAX = 2x1 + x2 . Расписав условие									1	3	x		18
									AX ≤ B , т.е.	2	1		≤	,
									2		x2		16
	f1 = 6x1 +9x2 → max,
	f	2	= 2x		+ x → max,
			1			2
получим задачу:	x1 +3x2 ≤18,							.
	2x + 2x			2		≤16,
			1			≥ 0.
	x		≥ 0, x
	1		2

76

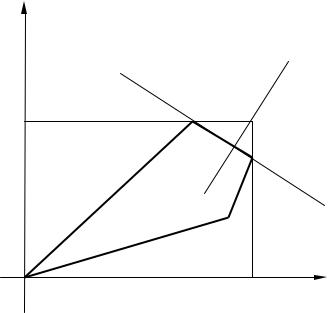
Введем

линейное

преобразование

f : R2 → R2 ,

определенное

критериями f1

и f2 :

f1 (x)

f (x)

6x +9x

6

9 x

=

=

1

2

=

1

.

f2 (x)

2x1 + x2

2

1 x2

0

f (A)=

6

9

0

54

63

f (C)=

48

При этом f (O)=

,

2

6

=

6

,

f (B)=

,

.

0

1

11

16

В силу линейности f

мы можем легко получить образ области D под

действием преобразования

f

на плоскости

( f1, f2 )

– это четырех-

угольник с вершинами в точках f (O),

f (A), f (B),

f (C). При этом

идеальной является точка I

с координатами (f1,max , f2,max ), не принад-

лежащая образу D в силу того, что оптимальные значения соответст-

f2

вующих

целевых

функ-

ций достигаются в раз-

личных точках.

m

n

Естественно

предполо-

f (A)

жить, что образом ком-

I

промиссной

точки

явля-

ется точка, принадлежа-

P

f (B)

щая D и ближайшая к I ,

т.е. основание перпенди-

куляра, опущенного из I

f (C)

на отрезок, соединяющий

точки f (A) и f (B). Най-

f (O)

дя уравнение прямой

m ,

f1

проходящей

через

эти

точки, а затем прямой n ,

ей перпендикулярной и проходящей через

I , получим, что точка

P = m ∩n имеет координаты

123

;

23

P

2

2

. Наконец, находим компро-

миссную точку как прообраз P :

6 9 −1

123/ 2

7 / 2

x* = f −1 (P)=

2 3/ 2

=

.

2 1

9 / 2

Задачи для самостоятельного решения

№77-81. Решить задачу многокритериальной оптимизации: а) методом идеальной точки;

б) методом обобщенного критерия (α1 = 2 , α2 =1); в) методом приоритетов.

77

f

= x

+3x

→ max

f1

= 3x1 + x2

1

1

2

→ max

f

= 2x

+ x

→ max

f2

= 2x1 +x2 → max

f

= x

+ 2x

→ max

f

1

= x

+3x

→ max

1

2

2

1

2

2

1

2

77.

− x1 + x2 ≤ 3

x1 + x2 ≤ 8

. 79.

x1 + x2

≤ 9

.

x1

+ x2

≤10

. 78. x

≤ 5

x

≤ 5

x1 ≤ 8

1

1

x

≤ 6

x

≤ 7

x

2

≤ 5

2

≥ 0

2

≥ 0

≥ 0

x

x

x1

1

1

≥ 0

x2 ≥ 0

x2 ≥ 0

x2

f1

= 2x1 +3x2

→ max

f

2

= x

− 2x

2

→ max

1

− 2x2

≤1

x1

80.

x1 + x2 ≥1

.

− x

+ x

2

≤1

1

x

≤ 3

1

x2 ≤ 2

x

≥ 0

1

≥ 0

x2

81. Для выпуска двух видов продукции используются два вида ре-

сурсов. Известны	2	1		- матрица нор расхода сырья,	Q=(1,2) –
	A =
		3
	1

цены на ресурсы, P=(5,12) – цена реализации продукции, B = 10 - за-

15

пасы ресурсов.

82. Рекламное агентство, в штате которого 10 человек, получило заказ на рекламу нового продукта на радио и ТВ. Основные данные об аудитории, стоимости рекламы и количестве занятых ее изготовлением агентов занесены в таблицу (на 1мин.):

		Радио	ТВ
	Рекламная аудитория (млн.	4	8
	чел.)
	Стоимость минуты (тыс. у.е.)	8	24
	Количество занятых агентов	1	2

Рекламное агентство решает задачу о максимизации возможной аудитории ( f1 ) и минимизации издержек на изготовление рекламы ( f2 )

при условии, что контракт запрещает использовать более 6 минут рекламы на радио. Найти компромиссное решение: а) методом приоритетов ( f1 f2 ), б) методом обобщенного критерия (α1 = 2,5 ,

α2 = 0,5 ).

78