
Контрольные задания
Задача
1. Даны
векторы
![]() и
и![]() в некотором базисе трехмерного
пространства. Показать, что векторы
в некотором базисе трехмерного
пространства. Показать, что векторы![]() образуют базис данного трехмерного
пространства и найти координаты вектора
образуют базис данного трехмерного
пространства и найти координаты вектора![]() в этом базисе.
в этом базисе.
 (1;2;3),
(1;2;3),
 (-1;3;2),
(-1;3;2), (7;-3;5),
(7;-3;5),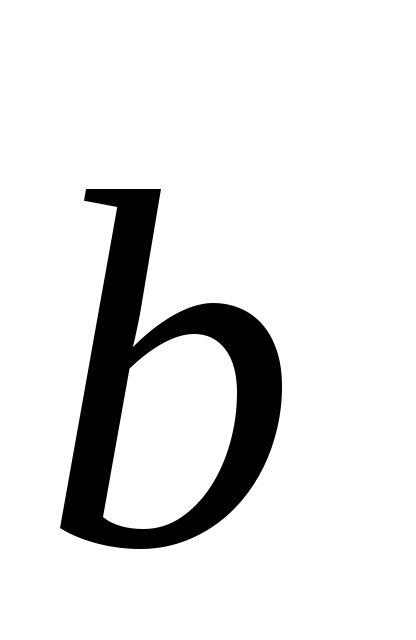 (6;10;17).
(6;10;17). (4;7;8),
(4;7;8),
 (9;1;3),
(9;1;3), (2;-4;1),
(2;-4;1),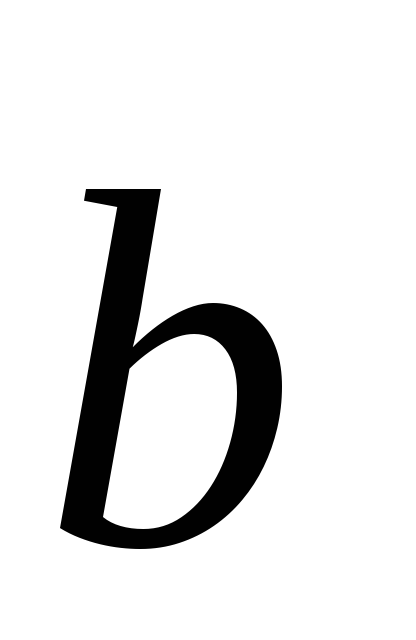 (1;-13;-13).
(1;-13;-13). (8;2;3),
(8;2;3),
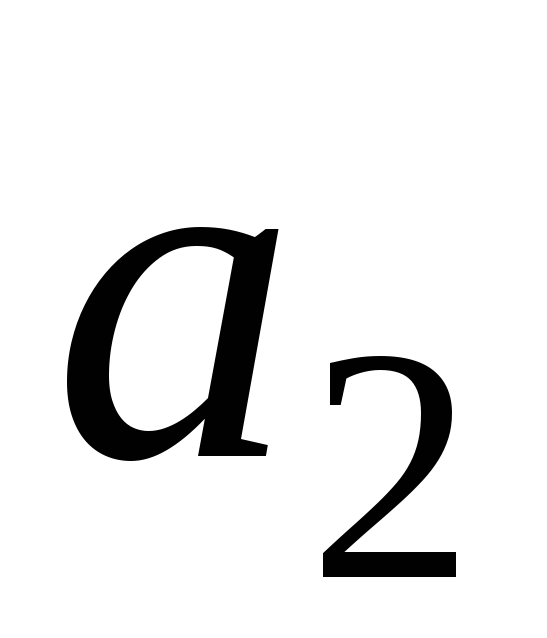 (4;6;10),
(4;6;10),
 (3;-2;1),
(3;-2;1),
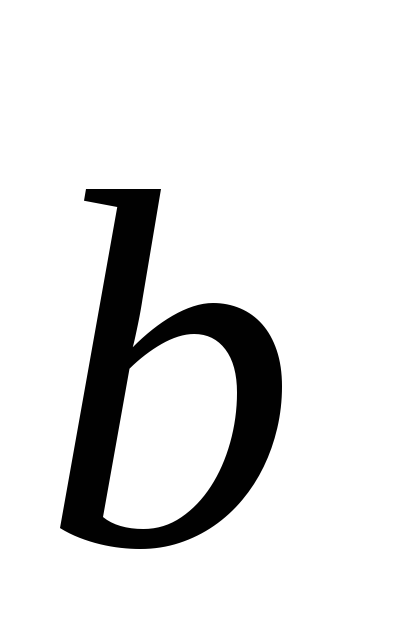 (7;4;11).
(7;4;11). (10;3;1),
(10;3;1),
 (1;4;2),
(1;4;2), (3;9;2),
(3;9;2),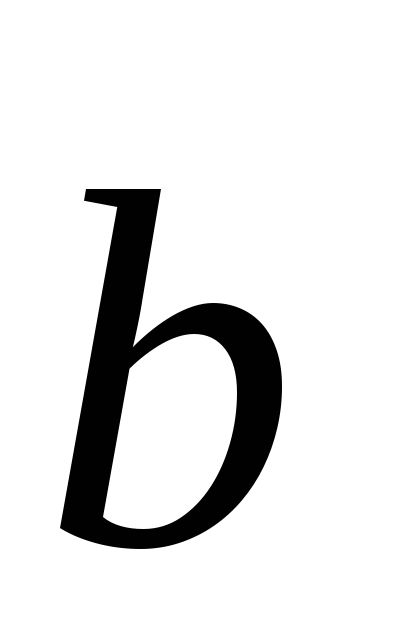 (19;30;7).
(19;30;7). (2;4;1),
(2;4;1),
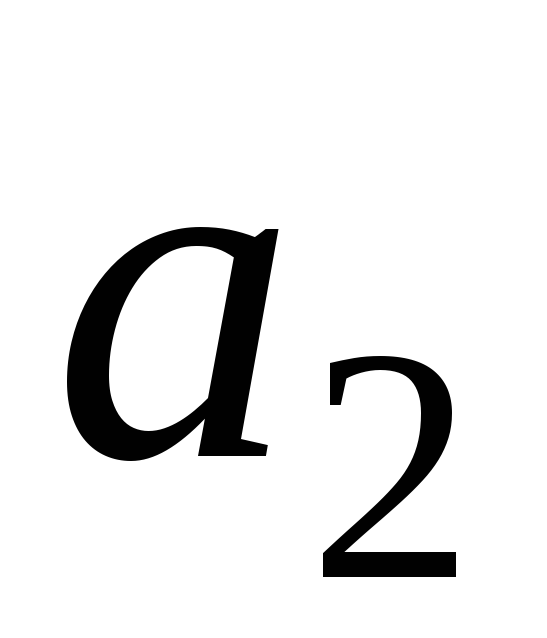 (1;3;6),
(1;3;6), (5;3;1),
(5;3;1), (24;20;6).
(24;20;6). (1;7;3),
(1;7;3),
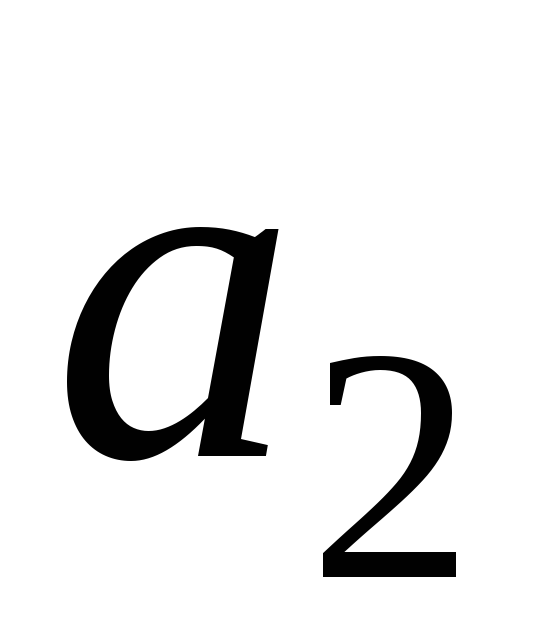 (3;4;2),
(3;4;2), (4;8;5),
(4;8;5), (7;32;14).
(7;32;14). (1;-2;3),
(1;-2;3),
 (4;7;2),
(4;7;2), (6;4;2),
(6;4;2),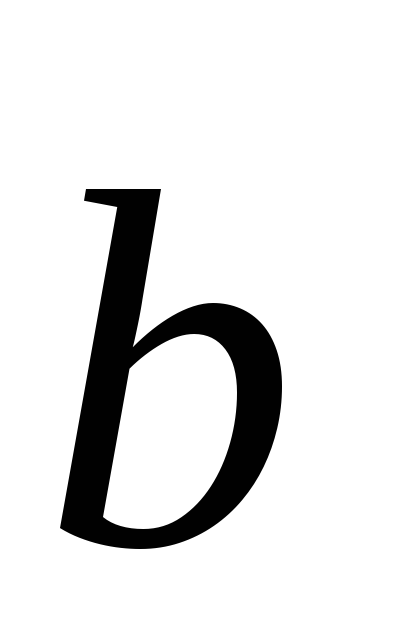 (14;18;6).
(14;18;6). (1;4;3),
(1;4;3),
 (6;8;5),
(6;8;5), (3;1;4),
(3;1;4), (21;18;33).
(21;18;33). (2;7;3),
(2;7;3),
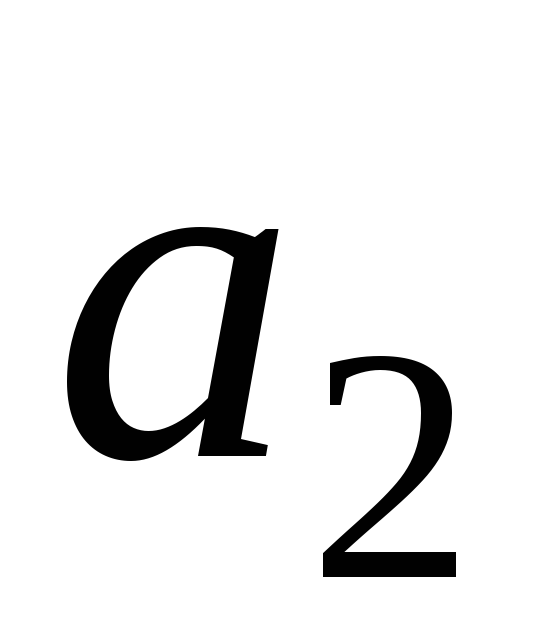 (3;1;8),
(3;1;8), (2;-7;4),
(2;-7;4), (16;14;27).
(16;14;27). (7;2;1),
(7;2;1),
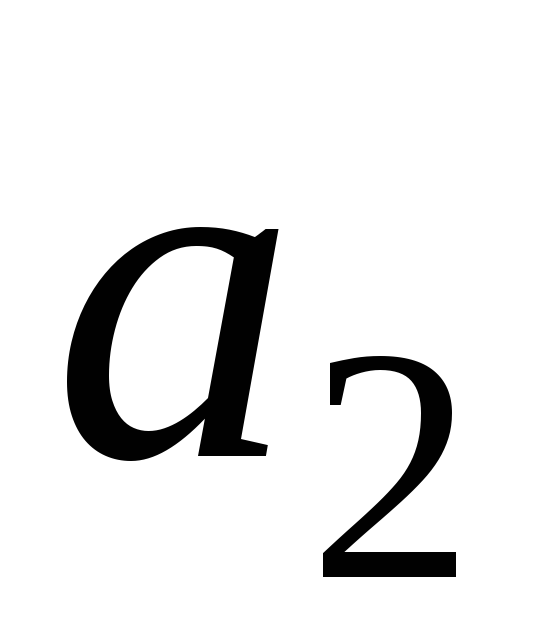 (4;3;5),
(4;3;5), (3;4;-2),
(3;4;-2),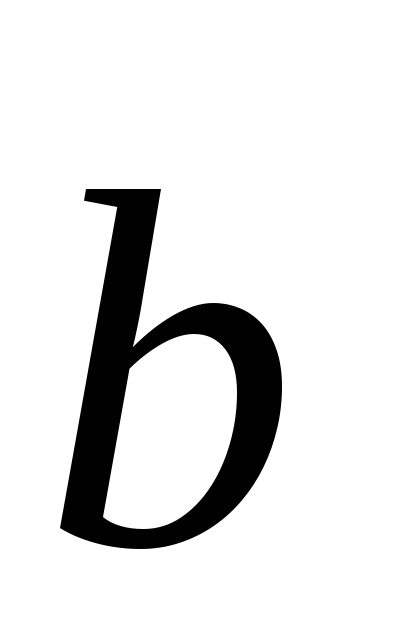 (2;-5;-13).
(2;-5;-13).
Задача
2. Даны векторы
![]() .
Показать, что векторы
.
Показать, что векторы![]() образуют базис четырехмерного
пространства, и найти координаты вектора
образуют базис четырехмерного
пространства, и найти координаты вектора![]() в этом базисе.
в этом базисе.
2.1.
![]()
![]()
2.2.
![]()
![]()
2.3.
![]()
![]()
2.4.
![]()
![]()
2.5.
![]()
![]()
2.6.
![]()
![]()
2.7.
![]()
![]()
2.8.
![]()
![]()
2.9.
![]()
![]()
2.10.
![]()
![]()
Задача
3. Даны вершины
![]() треугольника. Найти: 1) длину стороны
треугольника. Найти: 1) длину стороны![]() ;
2) внутренний угол
;
2) внутренний угол![]() в радианах с точностью до 0,001; 3) уравнение
высоты, проведенной через вершину
в радианах с точностью до 0,001; 3) уравнение
высоты, проведенной через вершину![]() ;
4) уравнение медианы, проведенной через
вершину
;
4) уравнение медианы, проведенной через
вершину![]() ;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины
;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины![]() ;
7) систему неравенств, определяющих
треугольник
;
7) систему неравенств, определяющих
треугольник![]() .
Сделать чертеж.
.
Сделать чертеж.
3.1.
![]() .
.
3.2.
![]() .
.
3.3.
![]() .
.
4.4.
![]() .
.
3.5.
![]() .
.
3.6.
![]() .
.
3.7.
![]() .
.
3.8.
![]() .
.
3.9.
![]() .
.
3.10.
![]() .
.
Задача
4. Даны
координаты вершин пирамиды А1А2А3А4.
Найти:1)длину ребра А1А2; 2) угол между
ребрами А1А2 и А1А4;![]() 3)
угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3; 5) объем пирамиды;
6) уравнение прямой А1А2; 7) уравнение
плоскости А1А2А3; 8)уравнение высоты,
опущенной из вершины А4 на грань А1А2А3.
Сделать чертеж.
3)
угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3; 5) объем пирамиды;
6) уравнение прямой А1А2; 7) уравнение
плоскости А1А2А3; 8)уравнение высоты,
опущенной из вершины А4 на грань А1А2А3.
Сделать чертеж.
4.1. А1(4;2;5), А2(0;7;2), А3(0;2;7), А4 (1;5;0).
4.2. А1(4;4;10), А2(4;10;2), А3(2;8;4), А4 (9;6;4).
4.3. А1(4;6;5), А2(6;9;4), А3(2;10;10), А4 (7;5;9).
4.4. А1(3;5;4), А2(8;7;4), А3(5;10;4), А4 (4;7;8).
4.5. А1(10;6;6), А2(-2;8;2), А3(6;8;9), А4 (7;10;3).
4.6. А1(1;8;2), А2(5;2;6), А3(5;7;4), А4 (4;10;9).
4.7. А1(6;6;5), А2(4;9;5), А3(4;6;11), А4 (6;9;3).
4.8. А1(7;2;2), А2(5;7;7), А3(5;3;1), А4 (2;3;7).
4.9. А1(8;6;4), А2(10;5;5), А3(5;6;8), А4 (8;10;7).
4.10. А1(7;7;3), А2(6;5;8), А3(3;5;8), А4 (8;4;1).
Задача 5 . Найти матрицу, обратную матрице
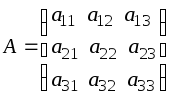 .
.
Проверить результат, вычислив произведение данной и обратной матриц.
5.1. 5.2.5.3.5.4.5.5.5.6.5.7.5.8.5.9.5.10.
Задача 6. Дана система линейных уравнений
![]()
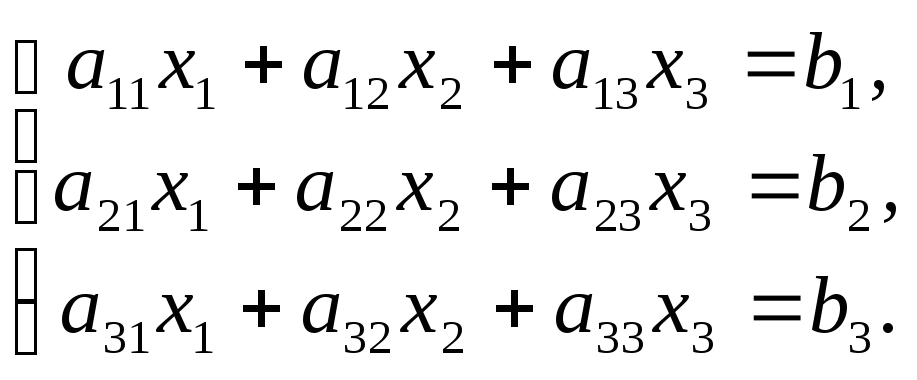
Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:
6.1.
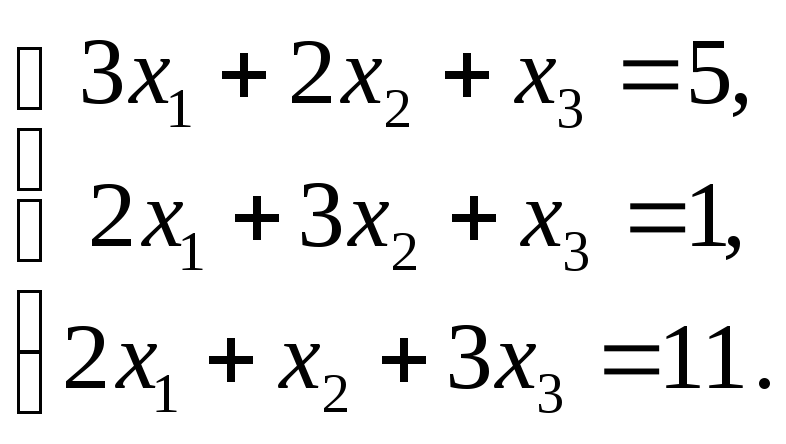 6.2.
6.2.
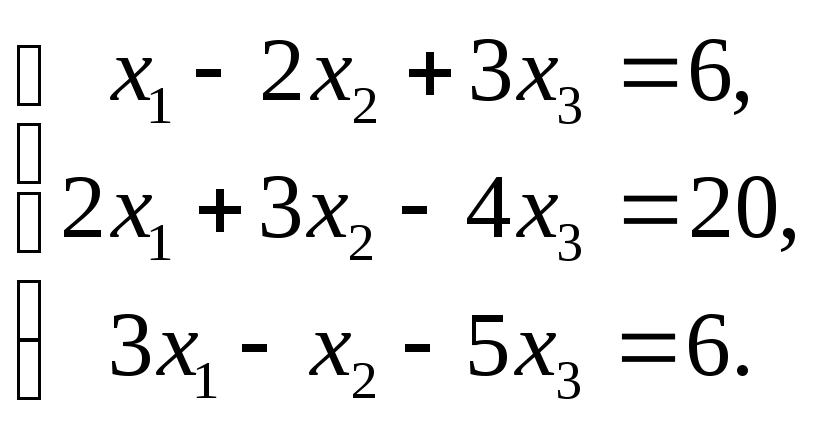
6.3.
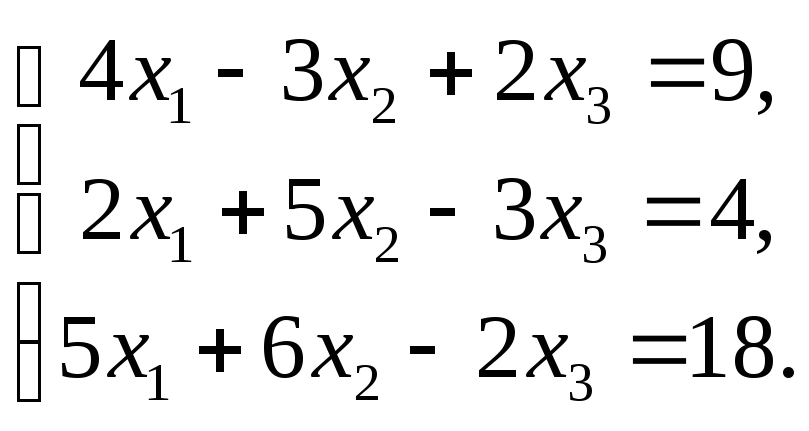 6.4.
6.4.
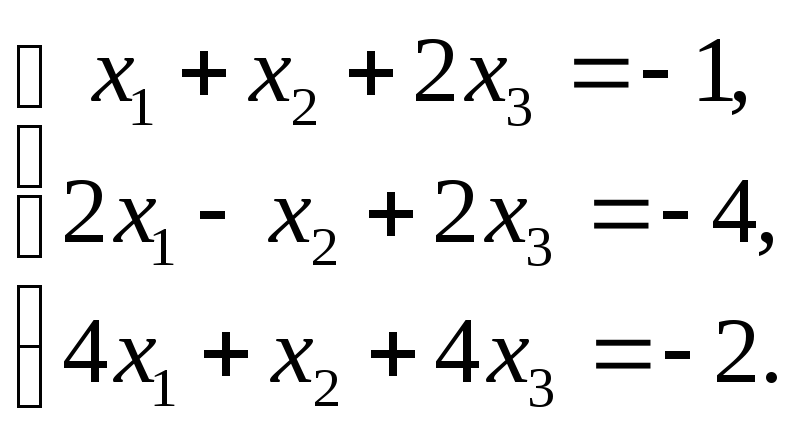
6.5.
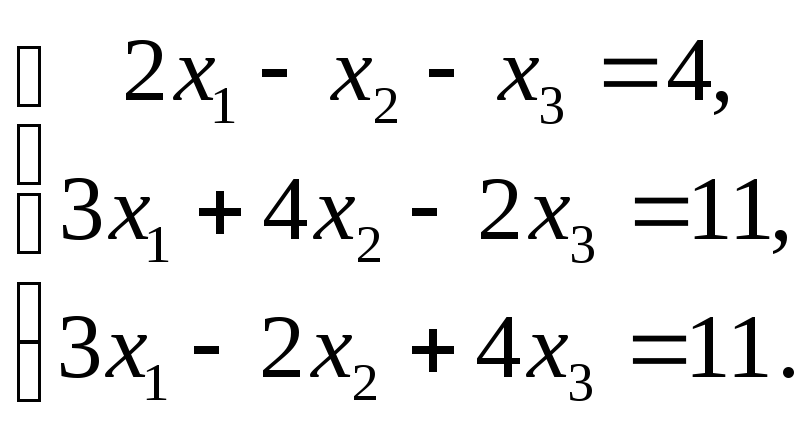 6.6.
6.6.
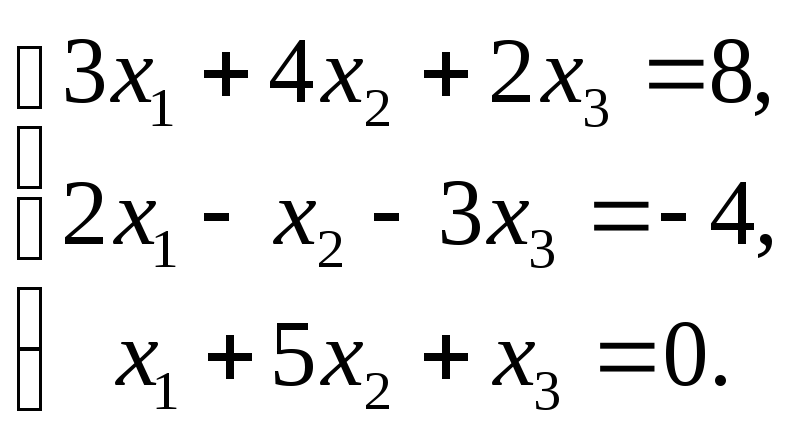
6.7.
 6.8.
6.8.
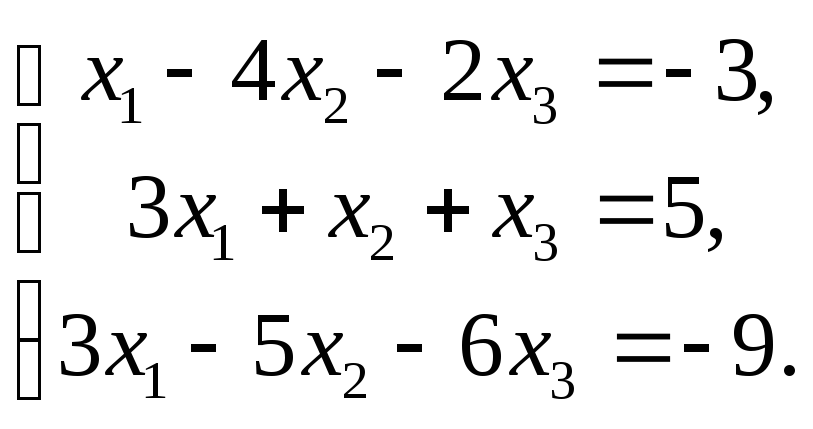
6.9.
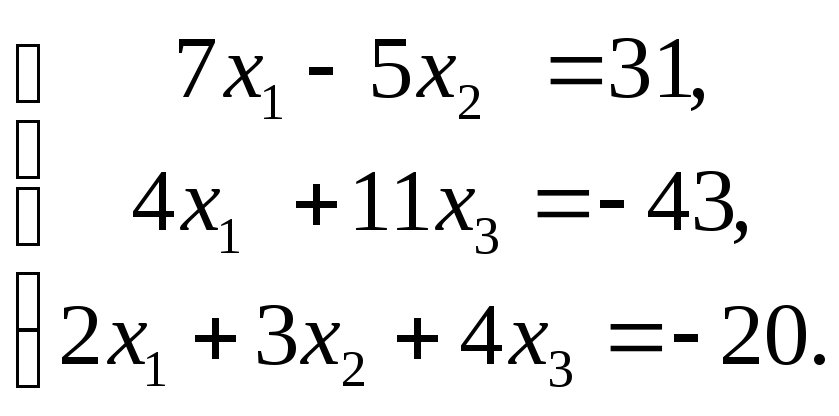 6.10.
6.10.

Решения типовых задач
Задача
1. Даны векторы
![]() ,
,
![]() ,
,
![]() и
и ![]() в некотором базисе трехмерного
пространства. Показать, что векторы
в некотором базисе трехмерного
пространства. Показать, что векторы ![]() образуют базис данного трехмерного
пространства и найти координаты вектора
образуют базис данного трехмерного
пространства и найти координаты вектора
![]() в этом базисе.
в этом базисе.
Решение.
Векторы ![]() образуют базис, если они линейно
независимы. Составим векторное равенство
образуют базис, если они линейно
независимы. Составим векторное равенство
![]() .
Записывая
.
Записывая ![]() в виде векторов – столбцов, получим
в виде векторов – столбцов, получим
![]() .
.
Задача свелась, таким образом, к решению системы
 .
.
Решим систему методом Гаусса.
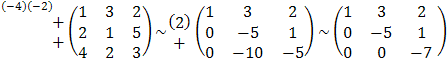 .
.
Итак, система приведена к виду
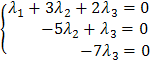 .
.
Полученная
система имеет единственное нулевое
решение:![]() , т.е. векторы
, т.е. векторы ![]() линейно независимы и, следовательно,
составляют базис. Вектор
линейно независимы и, следовательно,
составляют базис. Вектор ![]() можно представить в виде
можно представить в виде ![]() , т.е. координаты вектора
, т.е. координаты вектора ![]() в этом базисе
в этом базисе ![]() .
Для отыскания координат вектора
.
Для отыскания координат вектора ![]() решим систему линейных уравнений методом
Гаусса:
решим систему линейных уравнений методом
Гаусса:
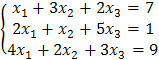 .
.
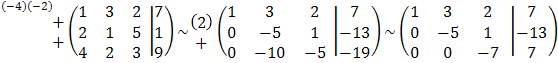 .
.
Итак, система приведена к виду
 .
.
Находим
![]() . т.е. вектор
. т.е. вектор ![]() .
.
Задача
2. Даны векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и ![]() .
Показать, что векторы
.
Показать, что векторы ![]() образуют базис четырехмерного
пространства, и найти координаты вектора
образуют базис четырехмерного
пространства, и найти координаты вектора
![]() в этом базисе.
в этом базисе.
Решение.
Векторы ![]() образуют базис, если они линейно
независимы. Составим векторное равенство
образуют базис, если они линейно
независимы. Составим векторное равенство
![]() .
Записывая
.
Записывая ![]() в виде векторов – столбцов, получим
в виде векторов – столбцов, получим
 .
.
Задача свелась, таким образом, к решению системы
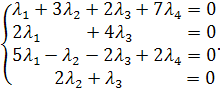
Решим систему методом Гаусса.

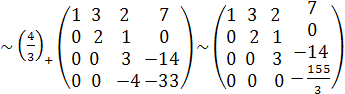 .
Итак, система приведена к виду
.
Итак, система приведена к виду  .
.
Полученная
система имеет единственное нулевое
решение: ![]() ,
т.е. векторы
,
т.е. векторы ![]() линейно независимы и, следовательно,
составляют базис. Вектор
линейно независимы и, следовательно,
составляют базис. Вектор ![]() можно представить в виде
можно представить в виде ![]() , т.е. координаты вектора
, т.е. координаты вектора ![]() в этом базисе
в этом базисе ![]() .
Для отыскания координат вектора
.
Для отыскания координат вектора ![]() решим систему линейных уравнений методом
Гаусса:
решим систему линейных уравнений методом
Гаусса:
 .
.

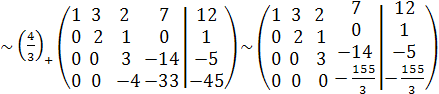 .
.
Итак, система приведена к виду
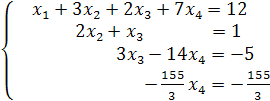 .
.
Находим
![]()
![]() ,
т.е. вектор
,
т.е. вектор ![]() .
.
Задача
3. Даны вершины
треугольника
![]() :
:![]() .
Найти: 1) длину стороны
.
Найти: 1) длину стороны![]() ;
2) внутренний угол
;
2) внутренний угол![]() в радианах с точностью до 0,001; 3) уравнение
высоты, проведенной через вершину
в радианах с точностью до 0,001; 3) уравнение
высоты, проведенной через вершину![]() ;
4) уравнение медианы, проведенной через
вершину
;
4) уравнение медианы, проведенной через
вершину![]() ;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины
;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины![]() ;
7) систему неравенств, определяющи
;
7) систему неравенств, определяющи х
треугольник
х
треугольник![]()
Решение.
1)
Длину стороны
![]() (длина
вектора
(длина
вектора![]() )
находим как расстояние между двумя
точками плоскости
)
находим как расстояние между двумя
точками плоскости![]() и
и![]() :
:![]() .
.
Поэтому
![]()
2)
Угол
![]() -
это угол между векторами
-
это угол между векторами![]() и
и![]() .
Координаты этих векторов:
.
Координаты этих векторов:![]() ,
,![]() .
Таким образом
.
Таким образом![]() .
.
Таким
образом, получаем
![]()
3)
Составим уравнение стороны
![]() :
:![]() ,
или
,
или![]() .
Угловой коэффициент стороны
.
Угловой коэффициент стороны![]() равен
равен![]() ;
следовательно, в силу условия
перпендикулярности, угловой коэффициент
высоты, проведенной из вершины
;
следовательно, в силу условия
перпендикулярности, угловой коэффициент
высоты, проведенной из вершины![]() ,
равен
,
равен![]() .
Уравнение этой высоты имеет вид
.
Уравнение этой высоты имеет вид![]() ,
получаем
,
получаем![]() ,
или
,
или![]() .
.
4)
Пусть точка М середина стороны
![]() .
Найдем ее координаты:
.
Найдем ее координаты:
![]()
![]() т.
т.![]() .
.
Уравнение
медианы
![]() находим с помощью уравнения прямой,
проходящей через две данные точки:
находим с помощью уравнения прямой,
проходящей через две данные точки: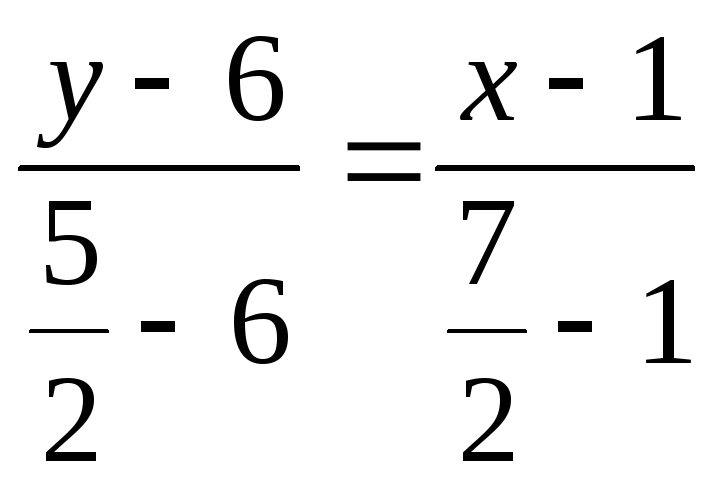 ,
получим
,
получим![]() .
.
5)
Составим уравнение еще одной высоты
треугольника
![]() .
Например, выберем высоту, проведенную
из вершины
.
Например, выберем высоту, проведенную
из вершины![]() .
Аналогично пункту 3) составим уравнение
стороны
.
Аналогично пункту 3) составим уравнение
стороны![]() :
:
![]()
![]()
![]() .
.
Угловой
коэффициент стороны
![]() равен
равен![]() ;
следовательно, в силу условия
перпендикулярности, угловой коэффициент
высоты, проведенной из вершины
;
следовательно, в силу условия
перпендикулярности, угловой коэффициент
высоты, проведенной из вершины![]() ,
равен
,
равен![]() .
Уравнение этой высоты имеет вид
.
Уравнение этой высоты имеет вид![]() ,
получаем
,
получаем![]() ,
или
,
или![]() .
Поскольку мы ищем точку пересечения
высот треугольника, то координаты этой
точки должны удовлетворять системе
уравнений
.
Поскольку мы ищем точку пересечения
высот треугольника, то координаты этой
точки должны удовлетворять системе
уравнений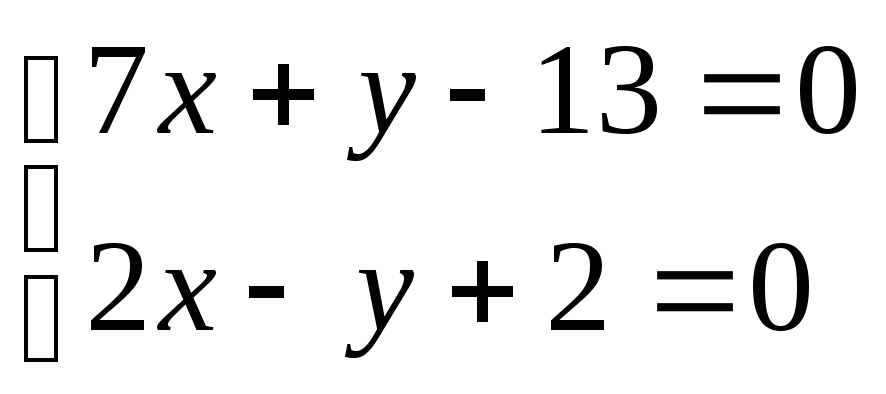 ;
;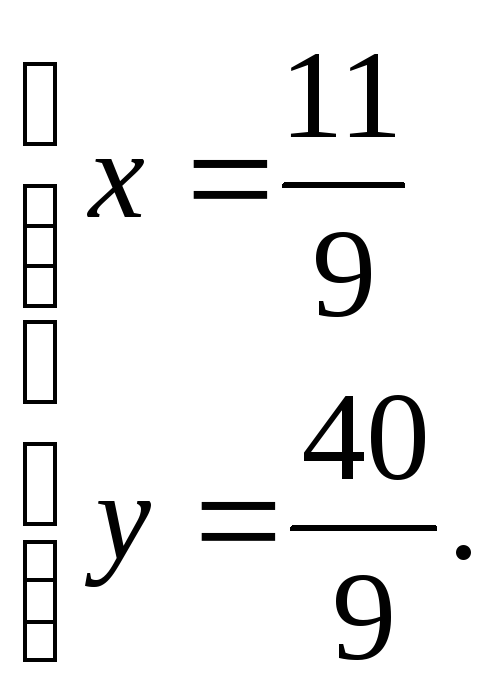 Таким образом, точка пересечения
высот треугольника
Таким образом, точка пересечения
высот треугольника![]() имеет координаты
имеет координаты![]()
6)
Найдем длину высоты, опущенной из вершины
![]() по формуле расстояния от точки
по формуле расстояния от точки![]() до прямой
до прямой![]() :
:![]() :
:![]() .
Таким образом
.
Таким образом
![]()
7)
Стороны треугольника
![]() заданы уравнениями прямых:
заданы уравнениями прямых:
![]() :
:
![]() ;
(см. пункт 3).
;
(см. пункт 3).
![]() :
:
![]() ;
(см. пункт 5).
;
(см. пункт 5).
![]() :
:
![]() ;
;![]() ;
;![]() .
.
Каждая
из этих прямых делит координатную
плоскость на две полуплоскости. Область
треугольника
![]() лежит выше прямой
лежит выше прямой![]() ,
т.е. в полуплоскости, которая задается
неравенством:
,
т.е. в полуплоскости, которая задается
неравенством:![]() .
Прямая
.
Прямая![]() делит координатную плоскость на две
полуплоскости, нам необходима та, которая
удовлетворяет неравенству:
делит координатную плоскость на две
полуплоскости, нам необходима та, которая
удовлетворяет неравенству:![]() .
Из двух полуплоскостей, которые разделяет
прямая
.
Из двух полуплоскостей, которые разделяет
прямая![]() ,
выбираем ту, которая задается неравенством:
,
выбираем ту, которая задается неравенством:![]() .
.
Таким
образом, область треугольника
![]() ,
определяется системой неравенств:
,
определяется системой неравенств: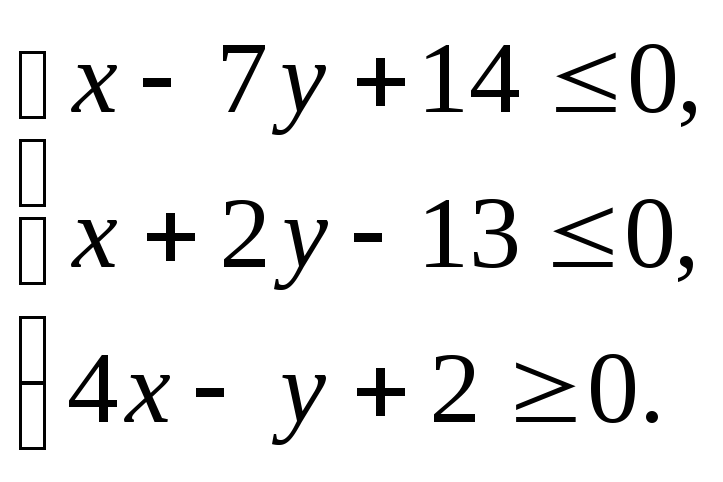
Задача
4. Даны
координаты вершин пирамиды ![]() :
:
![]()
![]() .
Найти:
.
Найти:
длину ребра
 ;
;
угол между ребрами
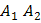 и
и 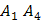 ;
;угол между ребром
 и гранью
и гранью 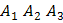 ;
;
площадь грани
 ;
;объем пирамиды; 6) уравнение прямой
 ;
;
7)
уравнение плоскости ![]() ;
;
8 )
уравнение высоты, опущенной из вершины
)
уравнение высоты, опущенной из вершины![]() на грань
на грань ![]() .
Сделать чертеж.
.
Сделать чертеж.
Р
![]()



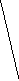
![]()
![]()
![]()

𝛽

![]()
![]()





,𝐴-2.
Длина ребра
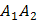 есть длина вектора
есть длина вектора 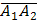 , координаты которого
, координаты которого 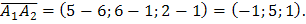 Т.к. длина вектора
Т.к. длина вектора  находится по формуле
находится по формуле 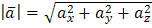 ,
то
,
то 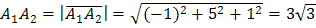 .
.Угол
 между ребрами
между ребрами  и
и 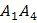 есть угол между векторами
есть угол между векторами
![]() =(-1,5,1)
и
=(-1,5,1)
и ![]() =(4-6;4-1;10-1)=(-2;3;9),
поэтому
=(4-6;4-1;10-1)=(-2;3;9),
поэтому ![]()
Отсюда
![]()
Обозначим угол между ребром
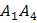 и гранью
и гранью 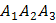 через
через  ,
тогда
,
тогда 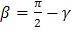 ,
где
,
где 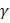 - угол между вектором
- угол между вектором 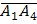 =(-2;3;9)
и нормальным вектором
=(-2;3;9)
и нормальным вектором  плоскости
плоскости  ,
которым является, например, векторное
произведение векторов
,
которым является, например, векторное
произведение векторов 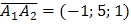 и
и 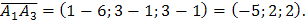
Т.к.
векторное произведение векторов
![]() =(
=(![]() )
и
)
и ![]() находится по формуле
находится по формуле  ,
то
,
то 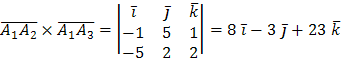 .
Итак,
.
Итак, ![]() .
Найдем теперь угол
.
Найдем теперь угол ![]()
![]() значит
значит
![]() или
или ![]()
4)
Т.к. длина векторного произведения двух
векторов равна площади параллелограмма,
построенного на этих векторах, как на
сторонах, то площадь S
грани ![]() (площадь треугольника) найдем как
половину площади параллелограмма,
построенного на векторах
(площадь треугольника) найдем как
половину площади параллелограмма,
построенного на векторах ![]() и
и ![]() как на сторонах, т.е. как половину длины
векторного произведения этих векторов.
как на сторонах, т.е. как половину длины
векторного произведения этих векторов.
Т.к.
![]() (см. пункт 3), то
(см. пункт 3), то
![]()
5)
Т.к. объем V
треугольной пирамиды, построенной на
векторах ![]() ,
находится по формуле
,
находится по формуле ![]() ,
где
,
где ![]() -
смешанное произведение векторов
-
смешанное произведение векторов ![]() ,
то
,
то
![]()
![]() .
Найдем смешанное произведение векторов
.
Найдем смешанное произведение векторов
![]() и
и ![]() по формуле
по формуле
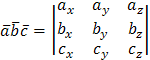 :
:
 (определитель вычислен по схеме
треугольников). Итак,
(определитель вычислен по схеме
треугольников). Итак, ![]() .
.
6)
Т.к. уравнение прямой, проходящей через
точку ![]() параллельно вектору
параллельно вектору ![]() имеет вид
имеет вид ![]() ,
то уравнение прямой
,
то уравнение прямой ![]() найдем как уравнение прямой, проходящей
через точку
найдем как уравнение прямой, проходящей
через точку ![]() в направлении вектора
в направлении вектора ![]() :
:
![]() .
.
7)
Т.к. уравнение плоскости, проходящей
через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() имеет вид
имеет вид ![]() (
(![]() нормальный вектор плоскости), то уравнение
плоскости
нормальный вектор плоскости), то уравнение
плоскости ![]() найдем как уравнение плоскости, проходящей
через точку
найдем как уравнение плоскости, проходящей
через точку ![]() с нормальным вектором
с нормальным вектором ![]() (см. пункт 3):
(см. пункт 3):
![]() или
или ![]()
8)
Уравнение высоты, опущенной из вершины
![]() на грань
на грань ![]() ,
найдем как уравнение прямой, проходящей
через точку
,
найдем как уравнение прямой, проходящей
через точку ![]() в направлении вектора
в направлении вектора ![]() -нормального
вектора плоскости
-нормального
вектора плоскости ![]() (см. пункт 3):
(см. пункт 3): ![]() .
.
Задача
5. Найти
матрицу, обратную матрице 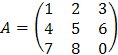 .
Проверить результат, вычислив произведение
данной и обратной матриц.
.
Проверить результат, вычислив произведение
данной и обратной матриц.
Решение.
Определитель матрицы ![]()
 ,
значит обратная матрица
,
значит обратная матрица ![]() существует. Найдем матрицу
существует. Найдем матрицу ![]() ,
транспонированную к
,
транспонированную к ![]() :
:
 .
Найдем алгебраические дополнения всех
элементов матрицы
.
Найдем алгебраические дополнения всех
элементов матрицы ![]() и составим из них присоединенную матрицу
и составим из них присоединенную матрицу
![]() .
.
![]()
![]()
![]()
 .
.
Найдем
обратную матрицу ![]() :
:
 .
.
Проверка:
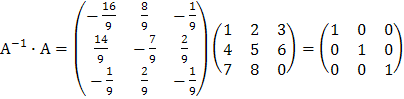 .
.
 .
.
Задача 6. Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
Решение.
1) Докажем совместность системы. Для
этого вычислим ранг матрицы А
исходной
системы и ранг расширенной матрицы
системы
![]()
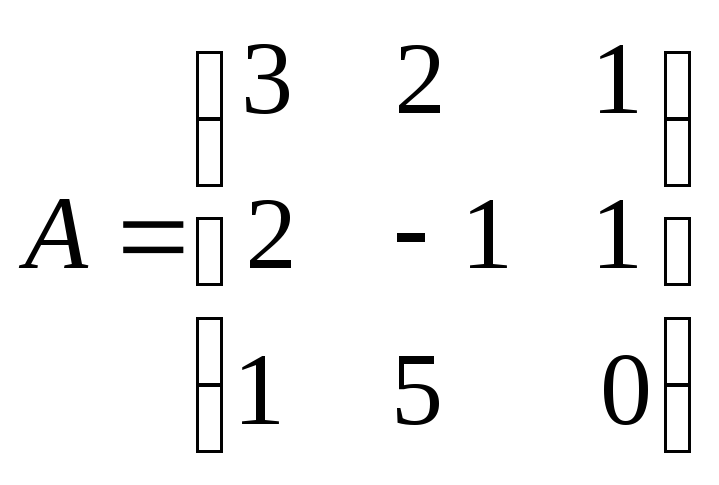
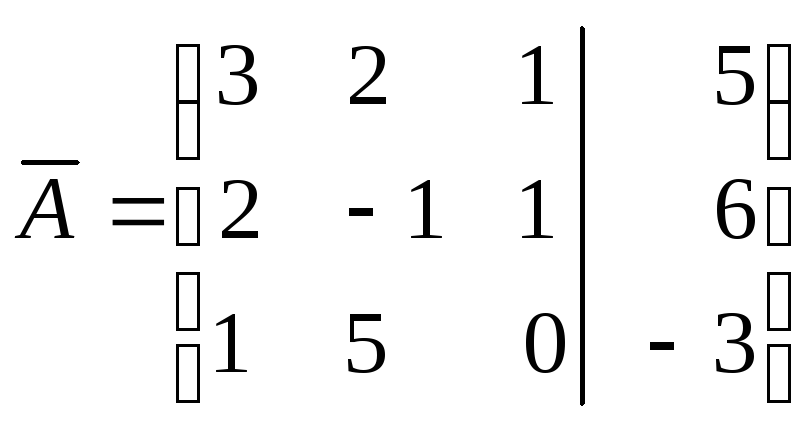
![]()
Д
2 3![]() :
:










 ~
~
 ~
~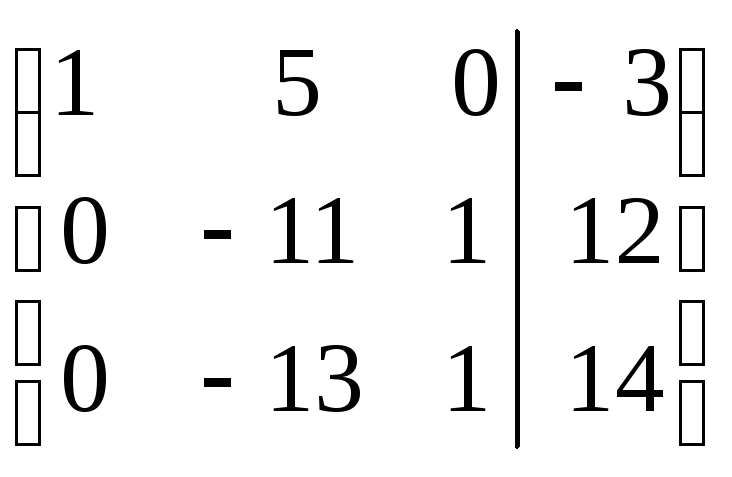 ~
~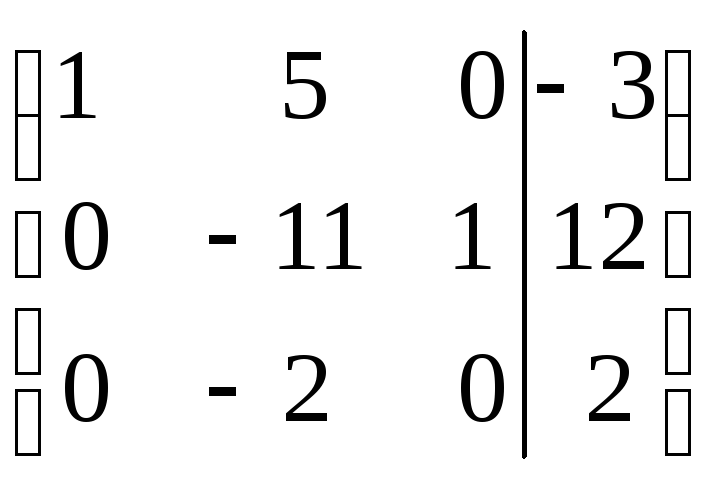
![]() т.е.
по теореме Кронекера-Капелли система
совместна.
т.е.
по теореме Кронекера-Капелли система
совместна.
2)
Решим систему методом Гаусса. Для этого
матрицу
![]() приведем к диагональному виду:
приведем к диагональному виду:

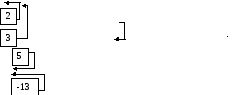
![]()
![]() тиии
тиии![]()
![]()
3) Решим систему матричным способом. Для этого введем следующие матрицы и исходную систему запишем в матричном виде.

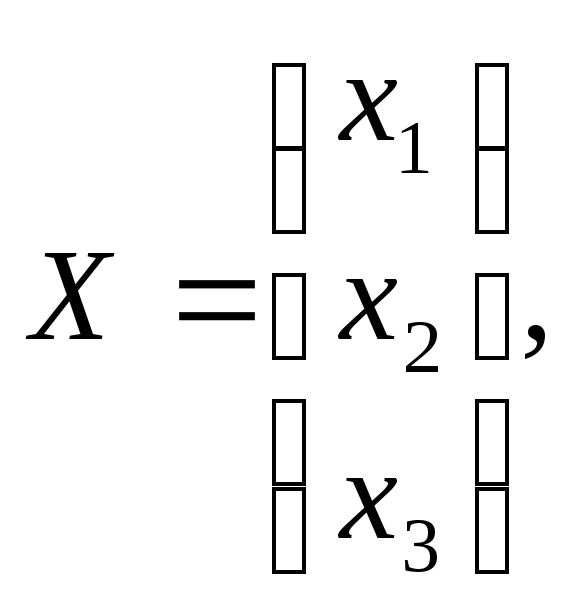
![]() .
.
![]()
Вычислим
обратную матрицу
![]() .
Определитель матрицыА
.
Определитель матрицыА
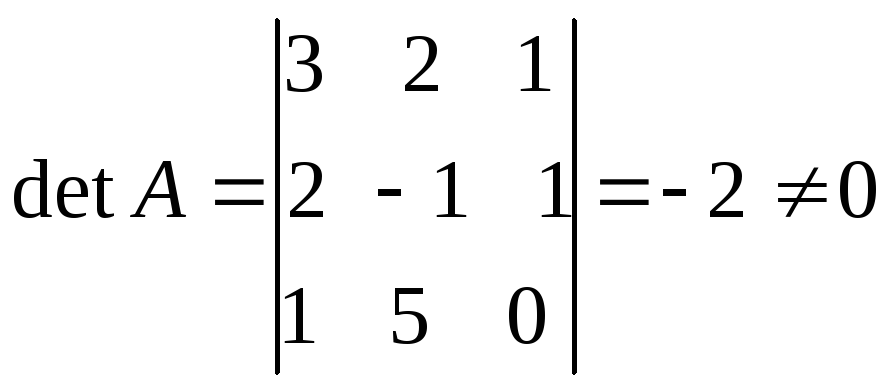 ,
значит обратная матрица существует.
Затем, вычислив к каждому элементу
матрицыА
алгебраические
дополнения, составим из них матрицу
,
значит обратная матрица существует.
Затем, вычислив к каждому элементу
матрицыА
алгебраические
дополнения, составим из них матрицу
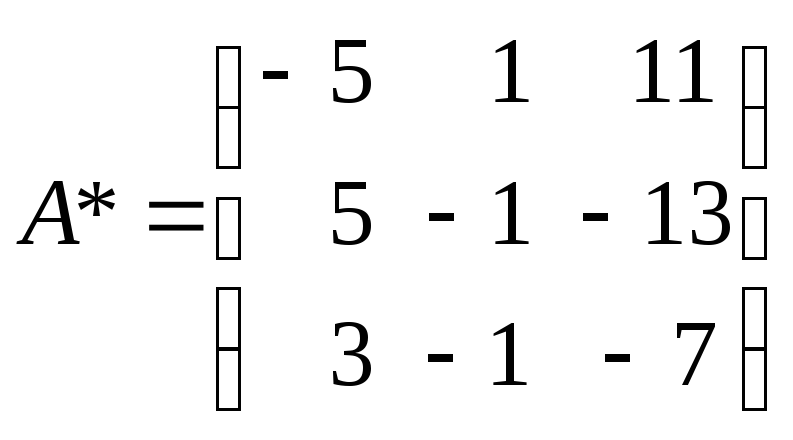 ,
транспонируем ее
,
транспонируем ее и находим обратную матрицу
и находим обратную матрицу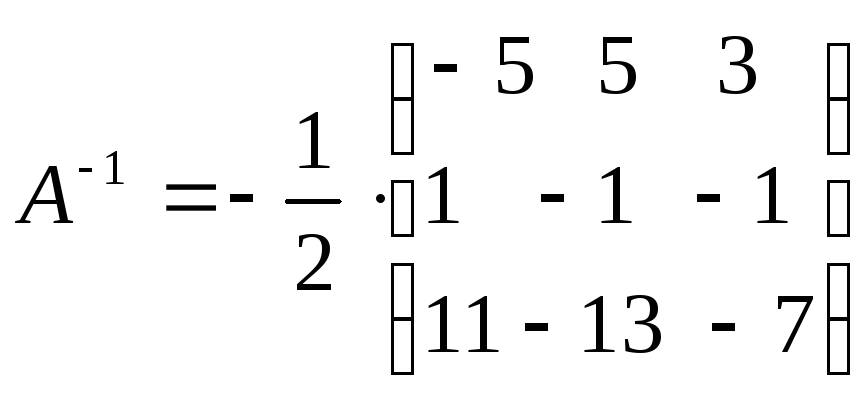
![]() .
.
![]()
=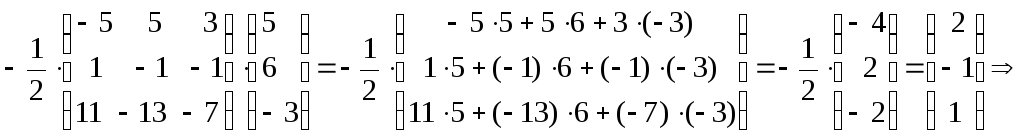
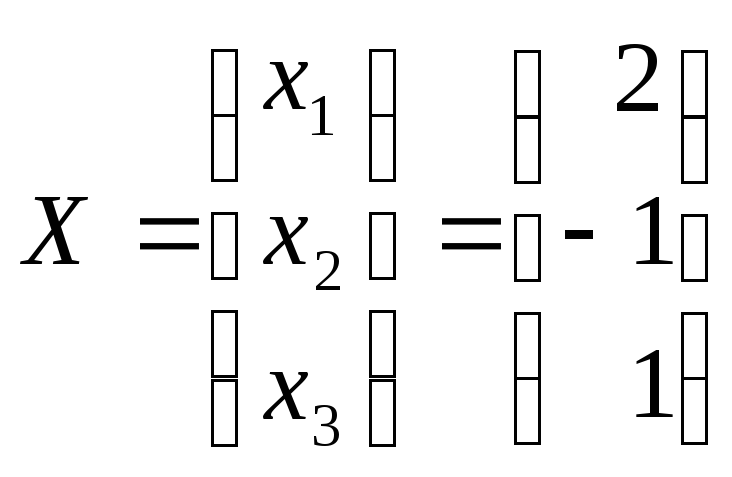 .
.
Ответ:
![]()
