2. Постановка задачи многомерной оптимизации. Основные понятия: линия уровня, градиент, антиградиент.

Задача, требующая нахождения оптимального значения функции m переменных f(Х)=f(x1, x2, …, xm), называется задачей многомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функции f на -f.

Множество точек, для которых целевая функция принимает постоянное значение f(x1, x2, …, xm) = c, называется поверхностью уровня. Для функции двух переменных (m = 2) это множество называется линией уровня.

Билет 13

Вопрос !) Постановка задачи численного интегрирования

Метод двойного просчета- чем маньше шаг h тем меньше R I^h, h/2,I^h/2

Уменьшение шага интегрирования (h) приводит к уменьшению погрешности.

Формула рунге

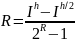
Выбор шагом метода наискорейшего спуска

14

1) Формула Симпсона. Геометрическая иллюстрация, вывод формулы, оценка погрешности

Для получения формулы Симпсона применяется квадратичный интерполирующий полином,

Оценка Погрешность метода в явном виде

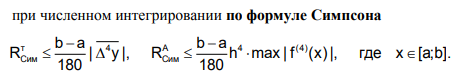
И оценка Погрешности в неявном k=4

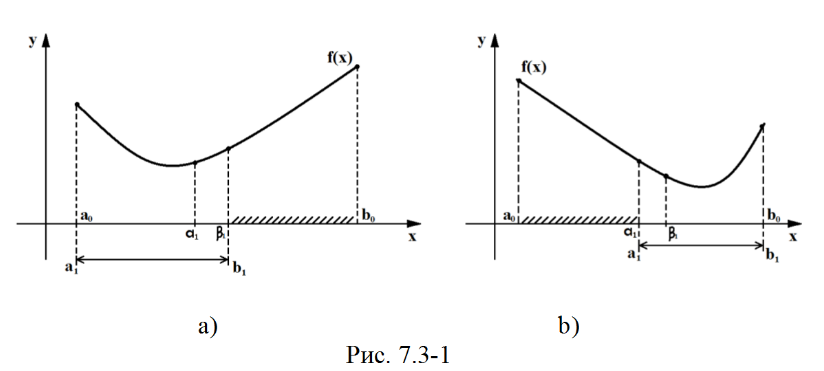
2)Постановка задачи одномерной оптимизации. Локальный и глобальный минимум

Задача оптимизации – одна из важнейших составляющих многих инженерных задач. Найти оптимальное решение – означает найти наилучший, в смысле заданного критерия, вариант из всех возможных. При решении задачи оптимизации рассматривается некоторая функция, называемая целевой (или критериальной), и аргументы (параметры целевой функции), называемые параметрами оптимизации.

Локальный минимум- это минимальное значение функции на заданном множестве

• глобальный минимум является наименьшим из локальных минимумов.

Билет 16

Вопрос 1) интерполяционная формула лагранжа

а) Достоинство – метод наиболее прост в понимании и организации вычислительного процесса. Основной недостаток метода – при увеличении числа узлов и соответственно степени интерполяционный многочлен Лагранжа требуется строить заново.

б) Достоинство – метод относится к числу итерационных методов и имеет наибольшую точность интерполяции. Основной недостаток метода – медленная скорость сходимости, что приводит к значительным затратам машинного времени.

в) Достоинство – использование многочленов невысокого порядка и вследствие этого малое накопление погрешностей в процессе вычислений. Основной недостаток метода – из числа методов интерполяции наиболее сложен в организации вычислительного процесса.

Вопрос 2)Метод дихотомии

17 Билет

Постановка задачи численного интегрирования.

Задача численного интегрирования заключается в нахождении значения определенного интеграла через ряд значений подынтегральной функции заданной в точках Причем, x0 = a, xn= b. Чаще всего интервал разбивают на подинтервалы длиной

Метод прямоугольников

Разбиваем промежуток интегрирования на 5, 10, 20 или бОльшее количество равных (хотя это не обязательно) отрезков, чем больше – тем точнее будет приближение

Вычисляем площадь полученной ступенчатой фигуры, которая и будет приближённой оценкой площади.

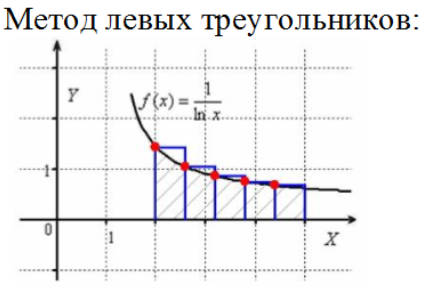
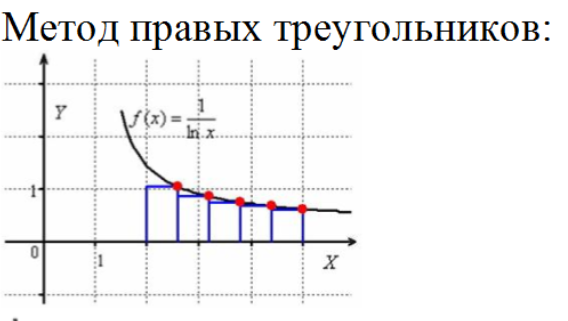
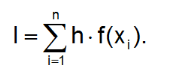
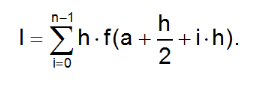
Оценка погрешности проводится с использованием метода двойного просчета, где в формуле Рунге k=2.

Метод золотого сечения

В основу метода положено разбиение отрезка неопределенности [a;b] в соотношении золотого сечения, такого, что отношение длины его большей части ко всей длине отрезка равно отношению длины его меньшей части к длине его большей части:

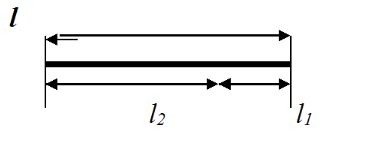
L2/L=L1/L2, где L=L1+L2, и L2>L1

L2=0.618, L1=L-L2=0.382

K1=L1/L=0.382 K2=L2/L=0.618

где k1, k2 - коэффициенты золотого сечения

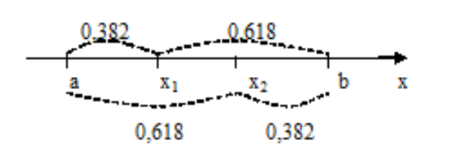
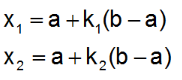
Находим x1 и x2, проверяем в какой из этих точек функция больше, затем отсекаем всю часть функции за данной точкой, данная точка становится началом отрезке. Проделываем эту операцию дальше

Геометрическая интерпретация метода золотого сечения

18

1)метод Рунге-Кутта 2-го порядка.

1 этап вычислить y|i+1=yi+h*f(xi,yi)

2 этап yi+1=yi+h*

Сначала находят грубое приближение по методу Эйлера (прогноз), а затем уточненное значение yi+1(коррекция).

происходит добивание точности в каждой точки

Погрешность метода Рунге-Кутты второго порядка связана с величиной шага интегрирования отношением e2 = C2h 3 , где C2 – произвольная постоянная.

Для оценки Погрешности решения Оду производиться при помощи нахождение решения дифференциального уравнения с шагом h/2

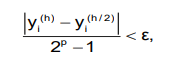p – порядок метода Рунге-Кутты в нашем случае 2

2)Градиентные методы наискорейшего спуска. Формулы. Сравнение

Суть метода состоит в следующем. Из выбранной точки (x₀,y₀) спуск осуществляют в направлении антиградиента до тех пор, пока не будет достигнуто минимальное значение целевой функции Q(x, y) вдоль луча (рис. 8.4-1). В найденной точке луч касается линии уровня. Затем из этой точки спуск проводится в направлении антиградиента (перпендикулярном линии уровня) до тех пор, пока соответствующий луч не коснется в новой точке, проходящей через нее линии уровня, и т.д.

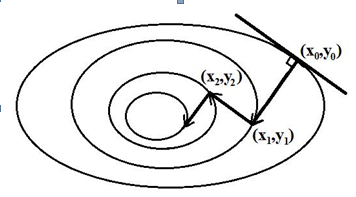
Н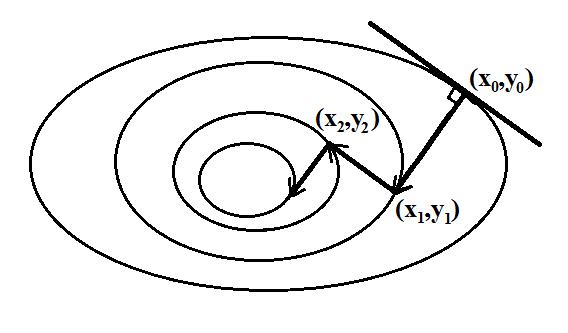 СА

(λ)  Q(x _k  λ_k  p_k ,y _k  λ_k s_k ).

Величина шага на каждой итерации определяется из условия минимума функции (λ):

(λ*) = min(  ()) _k=*(x_k, y_k), >0.

Таким образом, на каждой итерации выбор шага _k предполагает решение задачи одномерной оптимизации. По способу решения этой задачи различают:

НСЧ

НСЧ величину _k находят на отрезке [0;1] c заданной точностью, используя один из методов одномерной оптимизации (золотое сечение и дихотомия).

Уменьшаем отрезок ,до тех пора не будет выполнено условие погрешности, и шаг равен сумм a(конец отрезка слева) + b(конец отрезка справа) разделить пополам

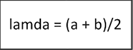
Отличие численного метода НС от аналитического состоит в том, что поиск значения  на каждой итерации происходит одним из известных численных методов одномерной оптимизации (например, методом дихотомии или методом золотого сечения). При этом в качестве интервала неопределенности служит диапазон допустимых значений € [0;1].

23