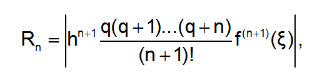1

1)Метод итераций для решения нелинейных уравнений. Способы улучшения сходимости

Представляет замену исходного уравнения f(x)=0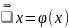

F(x)=x^2-2*x;

x^2-2*x=0

x= -

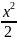
x=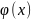

Если x корень НУ принадлежит отрезку [a;b] и построена последовательность приближений по правилу x_n=(x_n-1). Тогда, если все члены последовательности x_n=(x_{n -1}) [a;b] и существует такое q –максимум | (0<q<1),то процесс итераций сходиться к корню при любом начальном приближение  [a;b]

Если q<1 xn+1=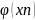

Если нет q>=1 то требуется провести улучшение сходимости

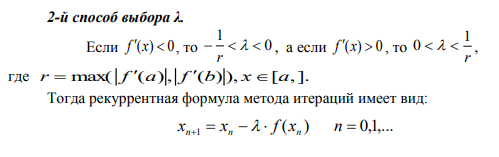
2) Геометрическая иллюстрация градиентного метода с дроблением шага(ГДШ)

Билет 5

Вопрос 1) методы прямоугольников для вычисления определенного интегралла

Вопрос 2) Унимодальность функции

Функция называется унимодальной, если она имеет единственный локальный минимум (максимум) на всей допустимой области. Для унимодальной функции локальный минимум (максимум) является также и глобальным.

какое условие нужно чтоб существовал минимум в одномерной функции

ответ Вторая производная положительна всегда

6

1. Постановка задачи численного решения нелинейного уравнения.

2. Постановка задачи одномерной оптимизации. Метод прямого перебора.

Одномерная оптимизация -  задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области. При решении задачи оптимизации рассматривается некоторая функция, называемая целевой (или критериальной), и аргументы (параметры целевой функции), называемые параметрами оптимизации.

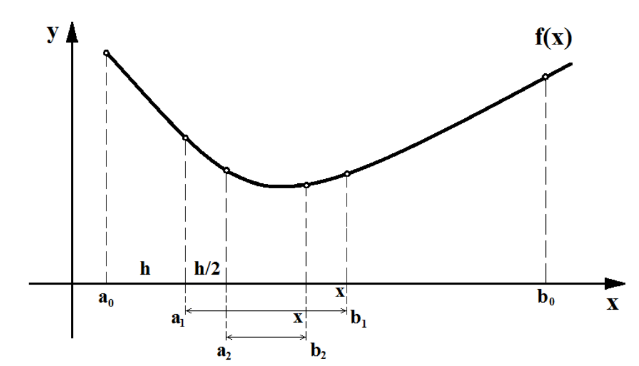
Суть метода прямого перебора заключается в следующем. От начальной точки интервала неопределенности [a,b] двигаются с начальным шагом (h) до тех пор, пока функция в точках разбиения уменьшается (т.е. функция убывает). Если функция в очередной точке стала возрастать, то происходит сужение интервала неопределенности путем возврата от рассматриваемой (которая станет правой границей нового интервала) точки x на два шага назад. При этом левой границей нового отрезка неопределенности станет точка a=x-2h, а правой b=x. Новый отрезок вновь исследуют таким же образом, но уже с уменьшенным в два раза шагом: h=h/2. Процесс повторяется до момента достижения заданной точности минимума |b_n-a_n| <.

7 Билет

Метод хорд

итерационный численный метод приближённого нахождения корня уравнения.

Суть метода хорд состоит в разбиении отрезка [a; b] (при условии f(a)f(b) < 0) на два отрезка с помощью хорды и выборе нового отрезка от точки пересечения хорды с осью абсцисс до неподвижной точки, на котором функция меняет знак и содержит решение, причём подвижная точка приближается к ε-окрестности решения.

За неподвижную точку в методе хорд выбирают тот конец отрезка [a;b], для которого выполняется условие

Таким образом, если за неподвижную точку приняли точку а, то в качестве начального приближения выступает х0 = b, и наоборот

Геометрическая интерпретация метода хорд

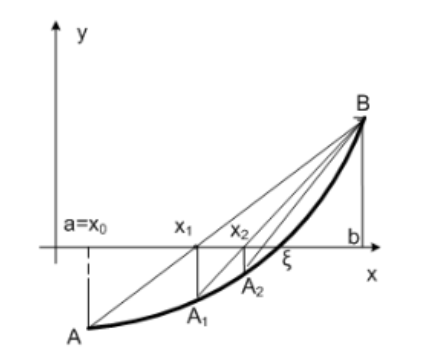
Проведем отрезок прямой через точки A и B. Очередное приближение x1 является абсциссой точки пересечения хорды с осью 0х. Построим уравнение прямой для этого случая:

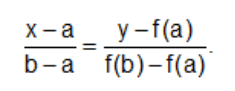
Положим y=0 и найдем значение х=х1 (очередное приближение):

Это и есть наша формула.

Погрешность

Оценка погрешности метода хорд определяется выражением

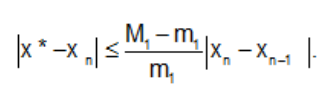
где m1 и M1 – соответственно наименьшее и наибольшее значения f'(x)

Условие окончания процесса итераций по методу хорд

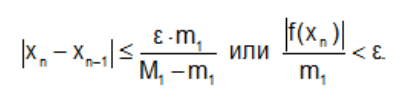
В случае, если M1<2m1, то для оценки погрешности метода может быть использована формула

Метод градиентного спуска с дроблением шага

На каждой итерации шаг спуска (лямбда к-тая) выбирается таким образом, чтобы выполнялось условие:

Выбор шага в методе ГДШ заключается в следующем.

Задается начальное значение шага lk = l0 (как правило, l0=0,5). Проверяется условие сходимости, приведенное выше. Если условие сходимости выполняется, то шаг спуска для данной итерации выбран, а если оно не выполняется, то принимают новый шаг lk = lk/2, и снова проверяют условие сходимости (и т.д.). (1 – это лямбда)

Алгоритм метода ГДШ можно описать следующей последовательностью действий:

1. При k = 0 задаемся начальной точкой спуска (xk, yk), требуемой точностью e и начальным шагом l0(пусть l0 =0,5).

2. Вычисляем значения

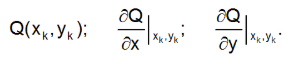
3. Вычисляем новые значения переменных

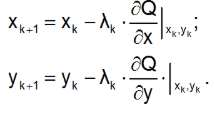
4. Проверяем условие сходимости:

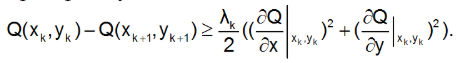
Если условие выполняется, то полагаем величину шага равной lk, в противном случае lk = lk/2 и переходим к п.3.

5. Проверка окончания процесса итераций (необходимого условия существования минимума):

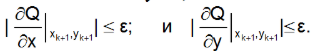
Если условие выполнено, то минимум найден, а если нет - вычисление координат следующей точки (k=k+1) и передача управления п.2.

Траектория спуска с использованием метода ГДШ приведена на Рис. 8.3-1.

12

1. 2-я интерполяционная формула Ньютона. Оценка погрешности.

Рассмотрим случаи, когда интерполируемая функция y=f(x) задается в равноотстоящих узлах так, что = x0 +ih, где h – шаг интерполяции, а i = 0, 1, …, n. В этом случае для нахождения интерполяционного многочлена могут применяться формулы Ньютона, которые используют конечные разности.

Оценка погрешности производится по формуле: