МАТАН ЭКЗАМЕН / 40 / условие выпуклости графиков функции

Для доказательства достаточно вспомнить, что  -- выпуклая функция и что .     

        Замечание 7.12   Теорема 7.11 проясняет тот факт, что условие  достаточно для наличия локального минимума в стационарной точке  функции . Действительно, из условия  следует, что функция  выпукла, то есть её график  "провисает вниз" в окрестности точки , в которой график имеет горизонтальную касательную. 

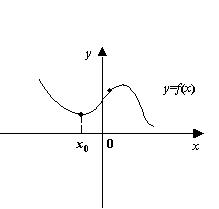
Рис.7.37.Выпуклость функции в окрестности точки минимума

Аналогично, график гладкой функции имеет выпуклость вверх в окрестности точки локального максимума. Поэтому неравенство  даёт достаточное условие локального максимума. 

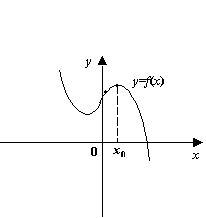
Рис.7.38.Вогнутость функции в окрестности точки максимума

    

Изучим теперь связь выпуклости и вогнутости функции  с взаимным расположением графика функции и касательных, проведённых к этому графику.

        Теорема 7.13   Пусть функция  имеет на интервале  производную . Функция  выпукла на  тогда и только тогда, когда график  лежит (при ) не ниже любой касательной , проведённой при любом , то есть выполняется неравенство

при всех .

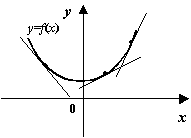
Рис.7.39.График выпуклой функции идёт не ниже любой своей касательной

        Доказательство.     Применяя формулу конечных приращений, получаем:

где  лежит между  и . Но по теореме 7.10 производная выпуклой функции не убывает, так что  при  и  при . В любом случае получаем, что произведение  неотрицательно, откуда . Отсюда следует неравенство из утверждения теоремы.      

        Замечание 7.13   Очевидно, что для вогнутых функций верно аналогичное утверждение:

дифференцируемая функция вогнута на интервале  тогда и только тогда, когда её график идёт не выше любой касательной:

при всех .     

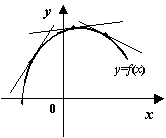
Рис.7.40.График вогнутой функции идёт не выше любой своей касательной

        Определение 7.6   Точкой перегиба функции  называется такая точка , которая разделяет два интервала  и , на одном из которых функция является выпуклой, а на другом -- вогнутой.     

Рис.7.41.Точка перегиба разделяет интервалы с разным направлением выпуклости

В случае, если вторая производная  непрерывна, в точке перегиба  непременно должно выполняться равенство , поскольку, согласно теореме 7.11,  должна менять знак при переходе через точку . Верно даже несколько более сильное утверждение:

        Теорема 7.14   Пусть  -- точка перегиба функции , причём существует . Тогда .

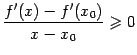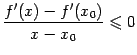        Доказательство.     Из существования  следует, что  существует при  из некоторого интервала , окружающего точку . По предположению, при достаточно малом , на интервалах  и  направление выпуклости функции разное; пусть для определённости  выпукла на  и вогнута на . Тогда функция  не убывает на  и не возрастает на , согласно теореме 7.10 и замечанию 7.9. Значит,  при  и  при . Переходя в этих двух неравенствах к пределу при базе  и  соответственно и замечая, что оба предела равны , получаем, что одновременно и . Значит, , что и требовалось доказать.      

Заметим однако, что не любая точка , такая что , обязана быть точкой перегиба: при переходе через такую точку функция  может и не сменить знак, тогда перегиба в точке  нет.

        Пример 7.32   Рассмотрим функцию ; её вторая производная  равна  и равняется 0 при . Однако поскольку  при всех , функция выпукла на всей оси , согласно теореме 7.11. Точка 0 не разделяет здесь интервалы разного направления выпуклости.     

Рис.7.42.Точка 0 не разделяет интервалы разного направления выпуклости функции 

        Пример 7.33   Рассмотрим функцию . Тогда  и  при  и  при . Точка  (в которой ) разделяет интервал вогнутости  и интервал выпуклости . Значит,  -- точка перегиба функции .     

Рис.7.43.Точка 0 -- точка перегиба функции 

        Пример 7.34   Рассмотрим функцию  Тогда  и  (при  вторая производная не существует). Тогда  при  и  при . Точка  (в которой  не существует) разделяет интервал вогнутости  и интервал выпуклости . Значит,  -- точка перегиба.     

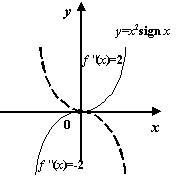
Рис.7.44.Точка 0 -- точка перегиба функции 

        Пример 7.35   Рассмотрим функцию . Тогда  (проверьте, что это так!). При  вторая производная (как и первая) не существует. Однако снова при  и  при . Значит,  -- точка перегиба.     

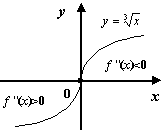
Рис.7.45.Точка 0 -- точка перегиба функции 

        Упражнение 7.2   Проверьте, пользуясь определением точки перегиба, что если  -- линейная функция (), то любая точка  есть её точка перегиба.

Проверьте, что любая точка  (в том числе ) есть точка перегиба функции .     

Итак, точки перегиба содержатся в списке тех точек , в которых либо , либо  не существует. Однако такая точка  может и не оказаться точкой перегиба; для выяснения нужно исследовать поведение функции слева и справа от "подозрительной" точки .