48. Стандартные ошибки оценок

Качество подбора функции регрессии можно оценить с помощью стандартных ошибок или дисперсий остатков и оценок параметров регрессии.

Стандартная ошибка или дисперсия остатков. Стандартная ошибка остатков называется также стандартной ошибкой оценки регрессии в связи с интерпретацией возмущающей переменной и как результата ошибки спецификации функции регрессии. Возмущающая переменная и является случайной с определенным распределением вероятностей. Математическое ожидание этой переменной равно нулю, а дисперсия — . Таким образом,— это дисперсия возмущения в генеральной совокупности. Нам неизвестны значения возмущающей переменной. Можно судить о ней только по остаткам. Вычисленная по этим остаткам дисперсияявляется оценкой дисперсии возмущающей переменной. Несмещенной оценкой дисперсии возмущающего воздействиябудет, следующее выражение:

(35)

В знаменателе формулы (35) стоит число степеней свободы , гдеn— объем выборки, am— число объясняющих переменных. Такое выражение числа степеней свободы связано с тем, что остатки должны удовлетворятьm + 1условиям. Кратко поясним это утверждение. Параметры множественной регрессии

(36)

вычисляют путем решения системы нормальных уравнений, в матричной форме записи имеющих вид

(37)

Подставим (36) в (37):

Раскрыв скобки и сделав соответствующие выкладки, получим

(38)

Матричное уравнение (38) содержит m + 1условий (уравнений), которые накладываются на остатки, и это приводит к уменьшению числа степеней свободы. Приk = 0в силу того, чтох₁ = 1для всехi,

(39)

что является следствием того, что математическое ожидание возмущающей переменной равно нулю. Из (38) при k = 1, … , m, т также получим

(40)

что вытекает из следующего: переменные x_k(k = 1, … , m) не коррелируют со значениями возмущения, т. е.x_k(k = 1, … , m) являются действительно объясняющими, а не подлежащими объяснению переменными. Следовательно, в регрессионном анализе могут обсуждаться только односторонне направленные зависимости. Поскольку термин «степень свободы» используется для обозначения независимой информации, в данном случае число связей, налагаемых наnнезависимых случайных наблюдений, можно интерпретировать какm + 1параметров (b₀, b₁ ..., b_m), которыми определяется функция регрессии.

В связи с тем что вычисление числителя в формуле (35) довольно затруднительно, мы хотим, опустив вывод, привести более простой способ его определения:

(41)

или в матричной форме записи:

Выражения сумм в правой части (41) содержатся в рабочей таблице для построения регрессии, а оценки параметров уже получены. Если снова обратиться к понятию коэффициента детерминации, введенному в разделах 1 и 2, то станет ясным физический смысл дисперсии (или стандартного отклонения) остатков — это та доля общей дисперсии , которая не может быть объяснена зависимостью переменной у от переменныхx_k(k = 1, … , m).

Стандартные ошибки или дисперсии оценок параметров регрессии. При описании этих показателей будем исходить из заданных значений объясняющих переменных.

Оценки параметров регрессии являются случайными величинами, имеющими определенное распределение вероятностей. Возможные значения оценок рассеиваются вокруг истинного значения параметра β. Определим меру рассеяния оценки параметра. Обозначим через матрицу дисперсий и ковариаций оценок параметров регрессии:

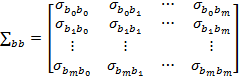(42)

Симметрическая матрица (42) на главной диагонали содержит дисперсии оценок параметров регрессии β_k,k = 0,1,…,m

(43)

а вне главной диагонали — их ковариации

(44)

для k≠lиk = 0,1,…,m, l = 0,1,…,m.

Краткая форма записи матрицы (42):

(45)

Подставив в (45) формулу (46)

(46)

получим

или

(47)

Далее, в силу того, что

(48)

имеем

(49)

Так как неизвестно, используем его оценку. В результате получаем оценку матрицы (49),

(50)

элементами главной диагонали которой являются искомые оценки дисперсий. Матрицу легко определить, поскольку матрицаизвестна (см. приложение Б), aвычисляется по (35).

Если мы обозначим через элемент главной диагонали матрицы, то оценка дисперсии параметра регрессии b_kбудет определяться выражением

(51)

т. е. она равна произведению дисперсии остатков на k-й элемент главной диагонали обратной матрицы,. Таким образом, стандартная ошибка оценки параметра регрессии b_kопределяется как

(52)

Найдем дисперсию и стандартную ошибку оценок параметров b₀и b₁простой линейной регрессии. В случае простой линейной регрессии имеем

.

а также

.

Согласно формуле (50) получим

.

Умножая на первый элемент главной диагонали матрицы, получим оценку дисперсии постоянной уравнения регрессии b₀:

(53)

а также ее стандартную ошибку:

(54)

Умножив на второй элемент главной диагонали матрицы, получим оценку дисперсии коэффициента регрессии b₁

(55)

а также стандартную ошибку этого коэффициента:

(56)

Рассмотрим более обстоятельно стандартную ошибку коэффициента b₁, простой линейной регрессии. Для этого сумму квадратов отклонений в (56) заменим на выражение, полученное путем преобразования формулы ():

Формула (56) приобретет вид

(57)

Итак, стандартная ошибка коэффициента регрессии зависит:

от рассеяния остатков. Чем больше доля вариации значений переменной у, необъясненной ее зависимостью отх, найденной методом наименьших квадратов, тем больше стандартная ошибка коэффициента регрессии. Следовательно, чем сильнее наблюдаемые значения переменнойуотклоняются от расчетных значений регрессии, тем менее точной является полученная оценка параметра регрессии;

от рассеяния значений объясняющей переменной х. Чем сильнее это рассеяние, тем меньше стандартная ошибка коэффициента регрессии. Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшом скоплении точек, близко расположенных друг к другу;

от объема выборки. Чем больше объем выборки, тем меньше стандартная ошибка коэффициента регрессии. Здесь существует непосредственная связь с таким свойством оценки параметра регрессии, как асимптотическая несмещенность.

Стандартная ошибка оценки параметра регрессии используется для оценки качества подбора функции регрессии. Для этого вычисляется относительный показатель рассеяния, обычно выражаемый в процентах:

(58)

Чем больше относительная стандартная ошибка оценки параметра, тем более оцененные величины отличаются от наблюдаемых значений зависимой переменной и тем менее надежны оценки прогноза, основанные на данной функции регрессии.

1