Простейшие двумерные преобразования
Точки на xy-плоскости можноперенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точкиР(х, у), которая перемещается в новую точкуР'(х, у), сдвигаясь наDx единиц параллельно осиx и на Dy единиц параллельно осиу, можно написать уравнения:
На рис. 2.1 показана точка с координатами (1, 2), которая смещается на расстояние (5, 7), преобразуясь в точку (6, 9). Определяя векторы-строки
можно переписать это уравнение в векторной форме или более кратко
Объект можно перенести, применяя вышевыведенное уравнения к каждой его точке. Однако, поскольку каждый отрезок, описывающий объект, состоит из бесконечного числа точек, такой процесс длился бы бесконечно долго. К счастью, все точки, принадлежащие отрезку, можно перенести путем перемещения одних лишь крайних точек отрезка и последующего вычерчивания нового отрезка между получившимися в результате точками. Это справедливо также для масштабирования (растяжения) и поворота. На рис. 2.1 показан результат действия на контур домика операции переноса на расстояние (3, -4).
Рис. 2.1 Простейший перенос
Точки можно промасштабировать (растянуть) вSx раз вдоль осиx: и вSyраз вдоль осиу, получив в результате новые точки, с помощью умножения
Определяя Sкак
, можно записать в матричной форме
или
На рис. 2.2 отдельная точка (6, 6) масштабируется с коэффициентами 1/2 по оси X и 1/3 по осиу. На этом же рисунке показан контур домика, промасштабированный с коэффициентами 1/2 по осиx и 1/4 по осиу. Отметим, что масштабирование производится относительно начала координат; в результате преобразования домик стал меньше и ближе к началу координат. Если бы масштабные множители были больше 1, то домик увеличился бы и отдалился от начала координат. Способы проведения масштабирования относительно других точек, отличных от начала координат, рассматриваются в одном из последующих разделов главы. Пропорции домика также изменились· было примененонеоднородное масштабирование, при которомSх≠ Sу. Однородное масштабирование, для которогоSx=Sy, не влияет на пропорции.
Точки могут быть повернуты на уголθ относительно начала координат, как показано на рис. 2.2 для точкиΡ (6, 1) и углаθ = 30°. Математически поворот определяется следующим образом:
В матричной форме мы имеем
или
где через R обозначена матрица поворота. На рис. 2.2 показан квадрат, повернутый на 45°. Как и в случае масштабирования, поворот производится относительно начала координат.
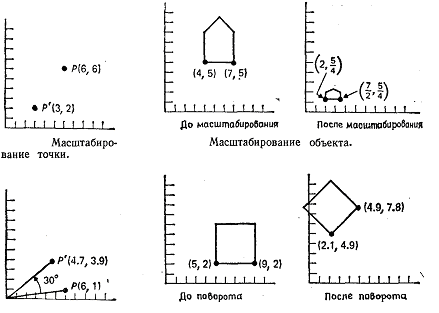
Рис. 2.2 Простейшие поворот и масштабирование
Однородные координаты и матричное представление двумерных преобразований
Преобразования переноса, масштабирования и поворота в матричной форме записываются в виде
К сожалению, перенос реализуется отдельно (с помощью сложения) от масштабирования и поворота (с помощью умножения). Хотелось бы представить их таким способом, чтобы все эти три элементарных преобразования можно было легко объединять вместе. Ниже в этом разделе показано, как это можно сделать.
Если мы выразим точки в однородных координатах, то все три преобразования можно реализовать с помощью умножений. Однородные координаты были введены в геометрии и впоследствии использованы в графике. С однородными координатами и преобразованиями над ними работают многие пакеты графических подпрограмм и некоторые дисплейные процессоры. В одних случаях эти координаты используются прикладной программой непосредственно при задании параметров для графического пакета, в других — применяются лишь внутри самого пакета и недоступны для программиста.
В однородных координатах точка Р (х, у) записывается какP(W∙ x, W ∙ y, W) для любого масштабного множителяW≠0. При этом если для точки задано ее представление в однородных координатахР(Х, Y, W), то можно найти ее двумерные декартовы координаты какx=X/W иy=Y/W. В этой главеW всегда будет равно 1, поэтому операция деления не требуется. Однородные координаты можно представить как вложение промасштабированной с коэффициентомW двумерной плоскости в плоскостьz=W (здесьz = 1) в трехмерном пространстве.
Точки теперь описываются трехэлементными вектор-строками, поэтому матрицы преобразований, на которые умножается вектор точки, чтобы получить другой вектор точки, должны иметь размер 3x3. Уравнения переноса записываются в виде матрицы преобразования однородных координат следующим образом:
где
Что будет, если точку Ρ
перенести в точкуР' на
расстояние(Dx1,
Dy1), а
затем вР" на расстояние(Dx2
Dy2).
Интуитивно ожидаемый результат в
этом случае представляет собой суммарный
перенос на расстояние(Dx1+Dx2,
Dy1+Dy2).
Чтобы доказать это, запишем данные в
виде
Теперь получим:
Матричное произведение Τ(Dx1, Dy1) ∙ T(Dx2, Dy2) есть
Действительно, результирующий перенос есть (Dx1+Dx2, Dy1+ Dy2). Матричное произведение в разных случаях называютобъединением, соединением, конкатенацией икомпозицией матрицT(Dx1, Dy2) иT(Dx2, Dy2). В этой главе мы будем использовать терминкомпозиция.
Уравнения масштабирования в матричной
форме записываются в виде
Определяя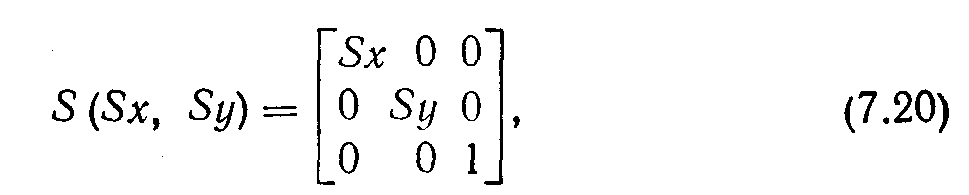
имеем
Так же как последовательные переносы являются аддитивными, можно ожидать, что последовательные масштабирования будут мультипликативными. Если заданы
то получим:
Матричное произведение S(Sx1, Sy1)∙S(Sx2, Sy2) есть
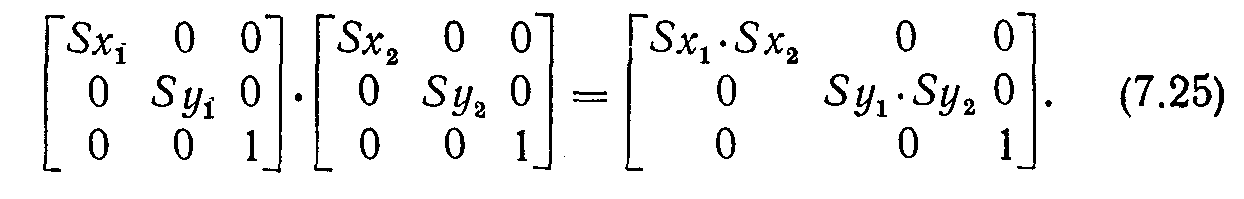
Таким образом, масштабирования в самом деле мультипликативны. И, наконец, уравнения поворота можно представить в виде:
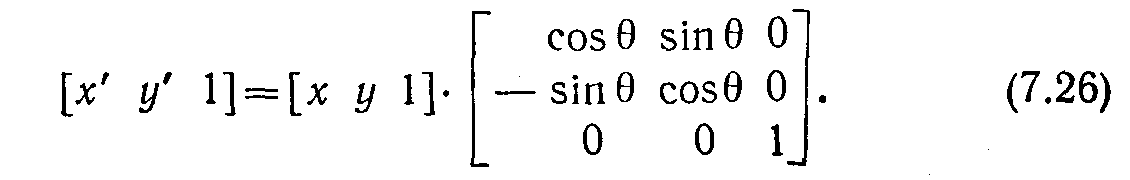
Полагая
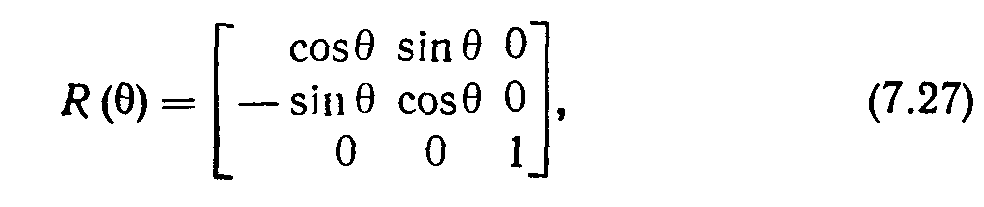
Имеем
