Лаба 2 3 4

Лабораторная работа № 2

Минимизация функции нескольких переменных

Ход работы:

Запускаем программму, вводим фамилию имя и вариант (рисунок 1).

Рисунок 1 – Окно запуска программы

Открывается окно выбор параметров расчета (рисунок 2). Согласно варианту заполняем:

начальное ребро симплекса = 1;

координаты начальной точки поиска – дальняя точка, абсцисса -11, ордината 11(по варианту);

метод построения симплекса – правильный;

точность расчета 0,0001.

Рисунок 2 – Выбор параметров расчета для дальней точки, по правильному симплексу

Кликаем на кнопку вычислить, и переходим в следующее окно программы (рисунок 3).

Рисунок 3 – Вычисление минимума функции для дальней точки по правильному симплексу

На рисунке 3 видим результат нахождения точки минимума для всех точностей от 1 до 0,0001. Далее выводим результаты вычислений (рисунок 4).

Рисунок 4 – Результаты расчета минимума функции по правильному симплексу для дальней точки

Заполним таблицу 1, по результатам расчета.

Таблица 1 – Значение функции после каждой итерации при достигаемой точности для дальней точки по правильному симплексу

№ итерации	Ребро симплекса	Достигаемая точность	x^0	x^1	x^2	f(x^0)	f(x^1)	f(x^2)
29	0.25	1	-2.88 1.967	-3.12 1.902	-3.06 2.143	0.7062	1.4619	1.6762
34	0.031	0.1	-2.99 1.995	-3.01 2.017	-3.02 1.986	0.0063	0.0284	0.0321
35	0.15	0.01	-3.007 2.006	-2.99 1.995	-3.007 1.991	0.0027	0.0063	0.0071
37	0.003	0.001	-2.99 1.99	-3.002 2.002	-3.002 1.99	0.00002	0.00006	0.00006
39	0.00156	0.0001	-3.005 2.0054	-2.99057 1.99	-3.00162 1..99036	0.00001	0.00002	0.00002

Далее проделываем такие же действия для ближней точки согласно варианту:

начальное ребро симплекса = 1;

координаты начальной точки поиска – ближняя точка, абсцисса -4, ордината

3(по варианту);

метод построения симплекса – правильный;

точность расчета 0,0001 (рисунок 5).

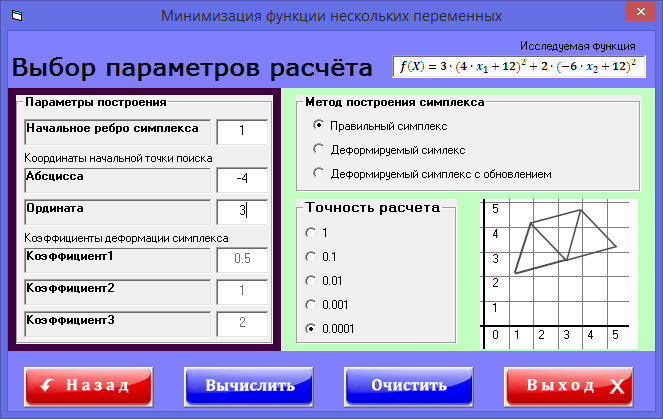
Рисунок 5 – Выбор параметров расчета для ближней точки, по правильному симплексу

Делаем расчет для выбранных параметров и получаем следующее (рисунок 6).

Рисунок 6 – Вычисление минимума функции по правильному симплексу для ближней точки

Выводим результат вычисления (рисунок 7).

Рисунок 7 – Результаты расчета минимума функции по правильному симплексу для ближней точки

Заполним таблицу 2 по результатам расчета для дальней и ближней точки.

Таблица 2 - Минимальное значение функции после каждой итерации при достигаемой точности для ближней и дальней точки по правильному симплексу.

Для дальней начальной точки				Для ближней начальной точки
Параметр точности	Число итераций	Координаты точки минимума	Значение функции в точке минимума	Параметр точности	Число итераций	Координаты точки минимума	Значение функции в точке минимума
1	29	-2.88 1.967	0.7062	1	8	-3.02773 2.02773	0.09226
0.1	34	-2.99 1.995	0.0063	0.1	12	-3.00563 2.00563	0.00381
0.01	35	-3.007 2.006	0.0027	0.01	14	-2.99458 1.99458	0.00352
0.001	37	-2.99 1.99	0.00002	0.001	18	-3.00011 2.00011	0
0.0001	39	-3.005 2.0054	0.00001	0.0001	20	-3.00011 2.00011	0

По исследованным данным найдем абсолютные и относительные погрешности для ближней и дальней точки по следующим формулам.

Абсолютная погрешность х=х_ист-х­_изм

Относительная погрешность

Где х_ист – теоритическая точка минимума;

х_изм – координата точки полученная в результате расчета;

n – число измерений или число итераций.

Заполним таблицу 3.

Таблица 3 – Абсолютная и относительная погрешности для правильного симплекса

Относительная погрешность					Абсолютная погрешность
Для дальней точки	Для ближней точки	Функция		Для дальней точки		Для ближней точки	Функция
		д.т.	б.т.				д.т.	б.т.
0,22 0,23	0,27 0,35	0,025	0,023	1,4 1,5		1,024 1,731	1,109	1,02
0,03 0,105	0,19 0,11	0,02	0,019	0,19 0,31		0,506 0,200	0,036	0,0075
0,06 0,018	0,075 0,083	0,01	0,002	0,108 0,012		0,088 0,088	0,0027	0,0039
0,05 0,01	0 0	0,002	0,001	0,0040 0,015		0 0	0	0
0 0	0 0	0	0	0 0		0 0	0	0

Вывод: Рассчитав минимум функции по правильному симплексу для ближней и дальней точки видим, что относительная и абсолютная погрешности невелики, а при достаточном числе итераций, для дальней точки 27-29, для ближней точки 13-14, погрешности и вовсе равны нулю.

Лабораторная работа № 3

Минимизация функции нескольких переменных

Ход работы:

Запускаем программу минимизация функции нескольких переменных и вводим начальные значения для дальней точки, но уже по деформируемому симплексу, согласно варианту и по способу построения – равносторонний треугольник (рисунок 1).

Рисунок 1 – Выбор параметров расчета для дальней точки по деформируемому симплексу

начальное ребро симплекса = 1;

координаты начальной точки поиска – дальняя точка, абсцисса -11, ордината 11(по варианту);

метод построения симплекса – деформируемый;

точность расчета 0,0001.

Нажимаем вычислить и переходим в следующее окно (рисунок 2).

Рисунок 2 - Вычисление минимума функции по деформируемому симплексу для дальней точки, способом равностороннего треугольника

Выводим результаты вычисления (рисунок 3).

Рисунок 3 – Результаты расчета минимума функции по деформируемому симплексу для дальней точки

Заполним таблицу 1 по результатам расчета для дальней точки.

Таблица 1 – Значение функции после каждой итерации при достигаемой точности для дальней точки по деформируемому симплексу, по способу равностороннего треугольника.

№ итерации	Достигаемая точность	x^0	x^1	x^2	f(x^0)	f(x^1)	f(x^2)
14	1	-2.9557 1.9277	-2.861 2.05335	-3.0142 2.1359	0.47057	1.1325	1.3403
18	0.1	-2.9749 2.0161	-3.0072 1.99665	-2,9969 1.9713	0,04817	0,0832	0,1027
22	0.01	-3,0016 2.0013	-2.9961 1.9954	-2.9873 2.0053	0,00024	0,00023	0,0097
25	0.001	-3,0159 2.0013	-2,9402 1,9912	-2,9505 2,0073	0,00024	0,00059	0,0006
28	0.0001	-3.0011 2.00131	-2,9971 1,9883	-3,012 1,9788	0,000542	0,000006	0,0001

Проделаем такие же расчеты для ближней точки (рисунки 4,5,6 и таблица 2).

Рисунок 4 – Выбор параметров расчета для ближней точки по деформируемому симплексу

начальное ребро симплекса = 1;

координаты начальной точки поиска – ближняя точка, абсцисса -4, ордината 3(по варианту);

метод построения симплекса – деформируемый;

точность расчета 0,0001.

Рисунок 5 – Вычисление минимума функции по деформируемому симплексу для ближней точки по способу равностороннего треугольника

Рисунок 6 – Результаты расчета минимума функции по деформируемому симплексу для ближней точки

Таблица 2 – Значение функции после каждой итерации при достигаемой точности для ближней точки по деформируемому симплексу способом равностороннего треугольника.

№ итерации	Достигаемая точность	x^0	x^1	x^2	f(x^0)	f(x^1)	f(x^2)
8	1	-3,0493 1.9563	-2.9741 2.0831	-3.0016 2.0881	0.2034	0.2525	0.5652
11	0.1	-3,0187 1.9921	-2,9611 2.0018	-3,0037 2,0912	0,02126	0,02313	0,09439
12	0.01	-2,9187 1,9665	-1,8609 0,8333	-2,1629 1,1629	0,0084994	0,01178	0,0133
18	0.001	-1,9974 0,9837	-2,0013 1,0314	-2,0338 1,9943	0,00006	0,00025	0,0003
20	0.0001	-2,0042 1,0118	-1,9974 0,9837	-2,0166 1,000	0,0000394	0,00007	0,0001

Теперь проделаем расчет по деформируемому симплексу способом построения по базисным векторам для дальней точки (рисунки 7 и 8).

Рисунок 7 – Выбор параметров расчета по деформируемому симплексу для дальней точки способом базисных векторов

начальное ребро симплекса = 1;

координаты начальной точки поиска – дальняя точка, абсцисса -11, ордината 11(по варианту);

метод построения симплекса – деформируемый;

точность расчета 0,0001

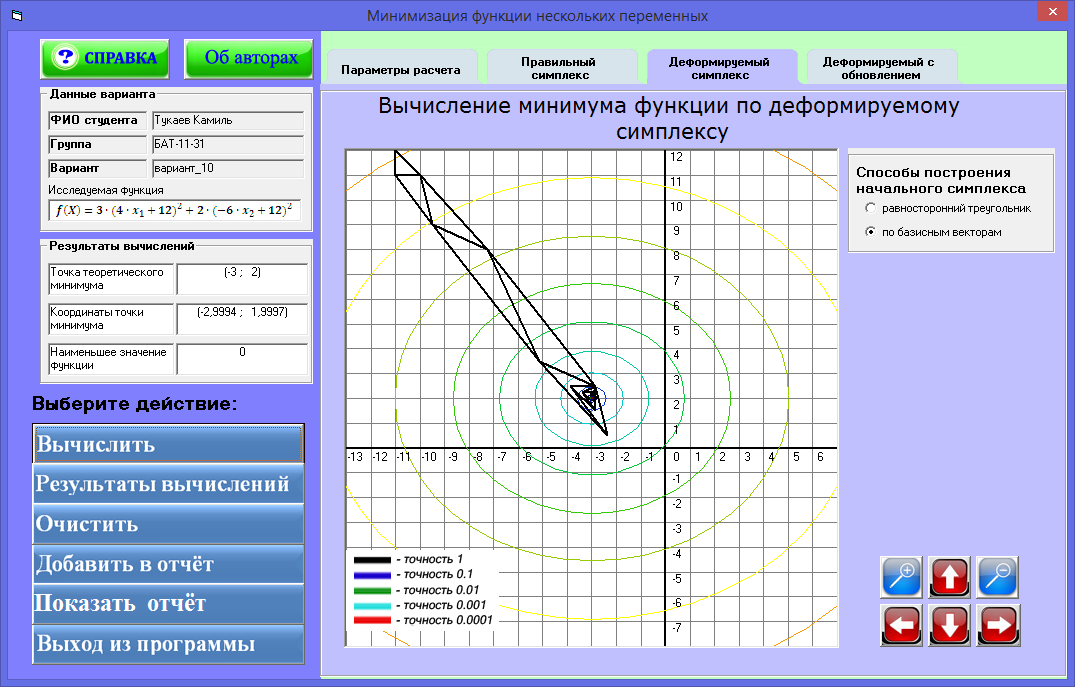
Рисунок 8 – Вычисление минимума функции по деформируемому симплексу для дальней точки по базисным векторам

Выведем результаты вычислений (рисунок 9).

Рисунок 9 – Результаты расчета минимума функции по деформируемому симплексу, для дальней точки по способу базисных векторов

Заполним таблицу 3

Таблица 3 – Значение функции после каждой итерации при достигаемой точности для дальней точки по деформируемому симплексу способом базисных векторов

№ итерации	Достигаемая точность	x^0	x^1	x^2	f(x^0)	f(x^1)	f(x^2)
14	1	-3,0625 1,91875	-2,9586 2,8008	-2,8156 2,0469	0,28601	0,4723	1,4139
17	0.1	-2,7649 1,9681	-2,0446 1,06606	-3,2884 2,1992	0,0149788	0,0293	0,0307
21	0.01	-2,0966 1,0317	-1,9876 0,8553	-1,7649 0,0681	0,002583	0,00528	0,015
24	0.001	-4,0226 3,0016	-1,9559 0,9876	-1,9938 0,937	0,0001285	0,00053	0,001
27	0.0001	-5,9803 4.0012	-2,0226 1,0016	-1,9869 1,0233	0,00009	0,00013	0,0002

Проведем аналогичные расчеты для ближней точки (рисунки 10,11,12 и таблица 4)

Рисунок 10 – Выбор параметров расчета по деформируемому симплексу для ближней точки способом базисных векторов

Рисунок 11 – Вычисление минимума функции по деформируемому симплексу для ближней точки по базисным векторам

Рисунок 12 – Результаты расчета минимума функции по деформируемому симплексу, для ближней точки по способу базисных векторов

Таблица 4 – Значение функции после каждой итерации при достигаемой точности для ближней точки по деформируемому симплексу способом базисных векторов

№ итерации	Достигаемая точность	x^0	x^1	x^2	f(x^0)	f(x^1)	f(x^2)
9	1	-3.0321 2.0332	-4.3462 3.1321	-4.3213 3.1321	1,251	1,25	2
12	0.1	-1,625 0,875	-2,0312 1,5938	-2,5 1,5	0,03906	0,0415	0,125
15	0.01	-1,8442 0,9155	-2,1641 1,1172	-1,9629 0,7949	0,00784	0,01016	0,0109
19	0.001	-4,9833 3,0108	-3,9694 2,975	-2,039 1,0139	0,00009	0,00039	0,0004
12	0.0001	-2,0077 1,0034	-1,9825 0,9911	-1,9833 0,0108	0,0000176	0,0001	0,0001

Таблица 5 - Минимальное значение функции после каждой итерации при достигаемой точности для ближней и дальней точки по деформируемому симплексу, способами начального построения: равносторонний треугольник и по базисным векторам.

Для дальней начальной точки								Для ближней начальной точки
Параметр точности	Число итераций		Координаты точки минимума		Значение функции в точке минимума		Параметр точности		Число итераций		Координаты точки минимума		Значение функции в точке минимума
Способ построения начального симплекса – равносторонний треугольник
1	5	-2.7746 -4.3656		0.17341		1				1		-3,0341 -5,7412		1,02525
0.1	8	-1,7525 -4,0672		0,0164		0.1				3		-1,1629 -2,1629		0,01326
0.01	11	-2,0691 3,8816		0,00269		0.01				5		-1,8187 -3,9665		0,0084994
0.001	13	-2,0159 -3,9662		0,000134		0.001				7		-1,9974 -3,9837		0,0000681
0.0001	17	-1,9919 -3,9965		0,00001		0.0001				13		-2,0042 -4,0118		0,0000394
Способ построения начального симплекса – по базисным векторам
1	9	-2,0625 -3,1875		0,16601		1				1		-3 -6		1,25
0.1	13	-1,7649 -4,0681		0,0149788		0.1				5		-1,625 -3,875		0,03906
0.01	15	-2,0966 -4,0317		0,002583		0.01				8		-1,8442 -3,9155		0,00784
0.001	19	-2,0226 -4,0016		0,0001285		0.001				13		-1,9833 -4,0108		0,0000992
0.0001	21	-1,9803 -4		0,00009		0.0001				15		-2,0077 -4,0034		0,0000176

По исследованным данным найдем абсолютные и относительные погрешности для ближней и дальней точки по следующим формулам.

Абсолютная погрешность х=х_ист-х­_изм

Относительная погрешность

Где х_ист – теоритическая точка минимума;

х_изм – координата точки полученная в результате расчета;

n – число измерений или число итераций.

Заполним таблицу 6 и 7.

Таблица 6 – Абсолютная и относительная погрешности для деформируемого симплекса по методу равностороннего треугольника.

Относительная погрешность					Абсолютная погрешность
Для дальней точки	Для ближней точки	Функция		Для дальней точки		Для ближней точки	Функция
		д.т.	б.т.				д.т.	б.т.
0,52 0,145	0,28 0,36	0,25	0,23	1,456 1,578		1,0268 1,458	1,203	1,350
0,11 0,059	0,25 0,37	0,026	0,014	0,194 0,236		0,506 0,196	0,056	0,0089
0,063 0,048	0,12 0,05	0,002	0,002	0,166 0,089		0,056 0,056	0,0036	0,0045
0,031 0,032	0,027 0,027	0,002	0,001	0,0056 0,0123		0 0	0	0
0,024 0,024	0 0	0	0	0 0		0 0	0	0