
- •Введение
- •Порядок выполнения работы задание
- •Задача 1 построение кривой д-разбиения
- •Задача 2 Определение области устойчивости
- •Задача 3 построение переходных процессов в аср
- •Задача 4 анализ качества регулирования при использовании различных законов регулирования
- •Приложение 1
- •Приложение 2 Методика обратного преобразования Лапласа для дробно-рациональных выражений
- •Приложение 3 Методика применения критерия Михайлова для исследования устойчивости аср
- •Приложение 4 Методика применения критерия найквиста для исследования устойчивости аср
- •Литература и электронные варианты учебных и справочных материалов
Приложение 2 Методика обратного преобразования Лапласа для дробно-рациональных выражений
Обратное преобразование Лапласа позволяет определять оригиналы (временные функции)по их изображениям. Для дробно-рациональных выражений передаточных функций получение оригинала производится в следующем порядке.
1.Записывается изображение выходной величины звена или системы
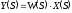

где
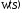 - передаточная функция звена ,
- передаточная функция звена ,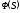 - передаточная функция замкнутой АСР
по какому-либо каналу воздействий
системы.
- передаточная функция замкнутой АСР
по какому-либо каналу воздействий
системы.
 - изображение входного воздействия.
- изображение входного воздействия.
В частности для единичного ступеньчатого воздействия

изображение определяется как
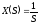 .
.
Для
воздействия

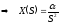 ,
где
,
где
2.
Разбиение изображения
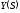 на элементарные слагаемыетабличного
вида.
на элементарные слагаемыетабличного
вида.
3.Определение оригиналов отдельных слагаемых по таблицам соответствия оригиналов и их изображений.
Итак, будем считать, что
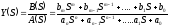
При
этом могут иметь место два случая
расположения корней характеристического
уравнения
 ,
при которых вид разложения различен:
,
при которых вид разложения различен:
а) корни простые;
б) корни кратные.
Сначала
рассмотрим разложение
 для простых корней.
для простых корней.
Разложение имеет вид

где
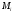 -
постоянные коэффициенты – константы
разложения сложной дроби на сумму
простых;
-
постоянные коэффициенты – константы
разложения сложной дроби на сумму
простых;
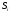 -
корни уравнения
-
корни уравнения
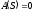 ,
,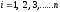 .
.
Оригинал этого изображения имеет вид

Среди простых корней, в свою очередь, могут быть нулевой, различные действительные и комплексно-сопряженные корни.
1.Один
нулевой корень
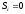 .
.
Тогда характеристический полином можно представить в виде
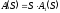
Коэффициент
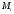 для этого корня определится как
для этого корня определится как
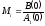
Оригинал слагаемого, соответствующего нулевому корню, будет иметь вид
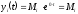
2.Корень
действительный

В этом случае

и представляет собой действительное число. Оригинал слагаемого, соответствующего действительному корню, будет иметь вид
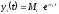
3.Корни
комплексно-сопряженные,
существуют парно 

или  .
.
В
этом случае коэффициенты
 ,
,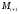 и слагаемые оригинала
и слагаемые оригинала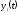 ,
, могут
вычисляться по формулам действительных
корней.
могут
вычисляться по формулам действительных
корней.
Однако,
учитывая, что
 ,
, в этом случае будут комплексно сопряженными
числами
в этом случае будут комплексно сопряженными
числами
 ,
,
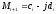
оригиналы
 ,
,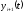 будут определяться
будут определяться
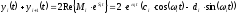 .
.
Для
случая, когда имеется корень
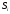 кратности
кратности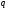 , можно записать
, можно записать
 ,
,
тогда можно записать

где

 ,
,
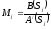 для
для
 .
.
Оригиналы каждого из первых слагаемых разложения для кратных корней вычисляются по формуле
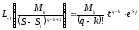 ,
где
,
где
 ,
,
оригиналы остальных членов по рассмотренным выше соотношениям

В
общем случае изображение
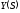 может иметь различные сочетания корней.
В этом случае для каждого типа корней
отдельно находятся слагаемые разложения,
оригиналы которых в сумме и дают оригинал
изображения
может иметь различные сочетания корней.
В этом случае для каждого типа корней
отдельно находятся слагаемые разложения,
оригиналы которых в сумме и дают оригинал
изображения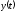 .
.
Пример.
Дано 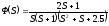 ,
,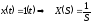 .
.
Определить
выходной сигнал АСР
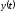 по заданию.
по заданию.
Решение.
Изображение регулируемой величины
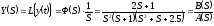
Корни
уравнения
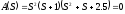
 кратности
кратности
 ;
;
 -
корень простой действительный,
-
корень простой действительный,
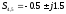 -
корни комплексно-сопряженные.
-
корни комплексно-сопряженные.
Разложение
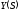 имеет вид
имеет вид
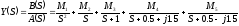
Расчет коэффициентов разложения по рассмотренным выше формулам
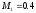 ,
,
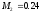 ,
,
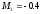 ,
,
 ,
,
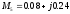 .
.
Оригиналы слагаемых
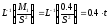
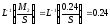


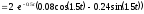
Оригинал
 равняется сумме оригиналов слагаемых
равняется сумме оригиналов слагаемых
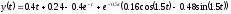
Приложение 3 Методика применения критерия Михайлова для исследования устойчивости аср
Критерий
Михайлова позволяет оценивать устойчивость
замкнутой АСР по известной частотной
характеристике замкнутой системы
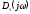 ,
которую принято называть годографом
Михайлова. Выражение годографа Михайлова
можно получить из характеристического
полинома замкнутой системы
,
которую принято называть годографом
Михайлова. Выражение годографа Михайлова
можно получить из характеристического
полинома замкнутой системы
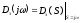
По
критерию Михайлова замкнутая АСР
устойчива, если годограф Михайлова,
начинаясь на положительной действительной
полуоси, проходит в положительном
направлении (по часовой стрелке)
последовательно с ростом частоты, ни
где не самопересекаясь и не обращаясь
в ноль, столько квадрантов 
 ,
какова степень характеристического
полинома
,
какова степень характеристического
полинома
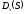 .
Рассматривается только положительный
диапазон частот
.
Рассматривается только положительный
диапазон частот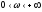 ,
так как на отрицательном диапазоне
годограф будет симметричен относительно
вещественной оси.
,
так как на отрицательном диапазоне
годограф будет симметричен относительно
вещественной оси.
Если
не выполнится хотя бы одно из этих
условий, замкнутая АСР будет не устойчива.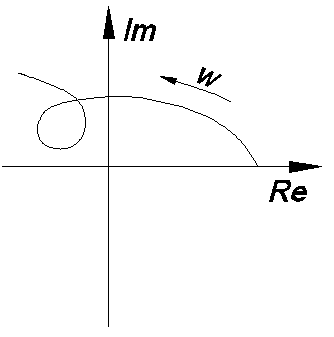
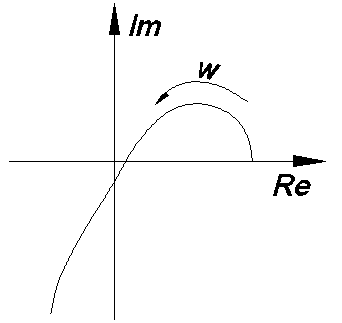

Если
годограф Михайлова пройдет через точку
начала координат, или начнется в ней,
система будет находится на границе
устойчивости.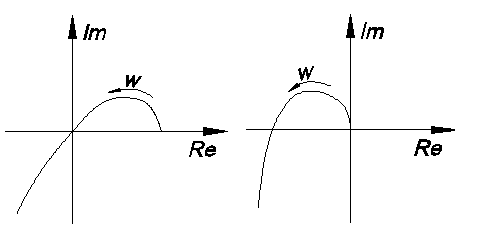
Таким
образом, чтобы оценить устойчивость
замкнутой АСР по этому критерию,
необходимо построить годограф
 на комплексной плоскости и оценить его
поведение на плоскости. Практически
это не всегда бывает удобно. Поэтому
чаще для решения задач на определение
устойчивости пользуются следствием
критерия Михайлова – свойством
перемежаемости корней многочлена
на комплексной плоскости и оценить его
поведение на плоскости. Практически
это не всегда бывает удобно. Поэтому
чаще для решения задач на определение
устойчивости пользуются следствием
критерия Михайлова – свойством
перемежаемости корней многочлена или методом чередования корней (под
корнями здесь понимаются не корни самой
системы, а корни выражений
или методом чередования корней (под
корнями здесь понимаются не корни самой
системы, а корни выражений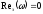 и
и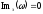 ).
).
Действительно,
если АСР устойчива, то ее годограф
Михайлова должен начаться на положительной
вещественной полуоси
 и последовательно пересекать полуоси
и последовательно пересекать полуоси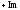 ,
,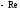 ,
, ,
,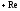 ,
, ,
,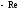 и т.д.. Причем частоты на которых происходят
эти пересечения должны последовательно
возрастать, а количество пересекаемых
полуосей соответствовать числу
и т.д.. Причем частоты на которых происходят
эти пересечения должны последовательно
возрастать, а количество пересекаемых
полуосей соответствовать числу .
Иначе это можно представить в виде
таблиц:
.
Иначе это можно представить в виде
таблиц:
для
АСР второго порядка
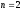 ,
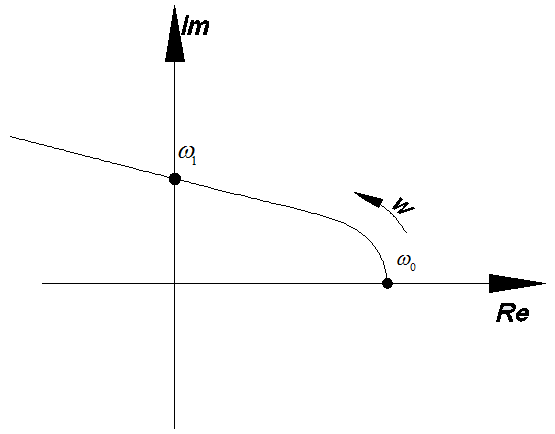
годограф Михайлова должен выглядеть
как на Рис.4, а пересечения годографа с
полуосями можно представить в виде
таблицы
,
годограф Михайлова должен выглядеть
как на Рис.4, а пересечения годографа с
полуосями можно представить в виде
таблицы

|
|
|
|
|
|
|
+ |
0 | |
|
|
0 |
+ |
РИС.4 Годограф Михайлова для АСР 2-го порядка
для
АСР третьего порядка 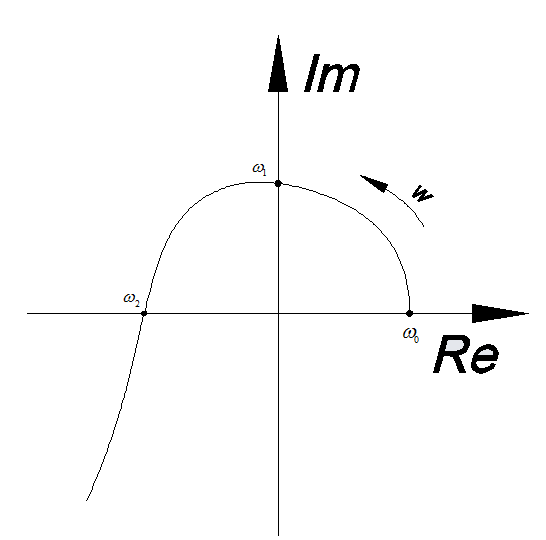
 ,
годограф Михайлова должен выглядеть
как на Рис.5, а пересечения годографа с
полуосями можно представить в виде
таблицы
,
годограф Михайлова должен выглядеть
как на Рис.5, а пересечения годографа с
полуосями можно представить в виде
таблицы
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
0 |
+ |
0 |
РИС.5 Годограф Михайлова для АСР 3-го порядка

для
АСР пятого порядка 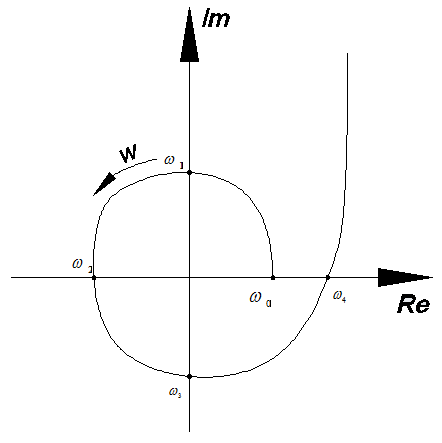
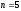 ,
годограф Михайлова должен выглядеть
как на Рис.6, а пересечения годографа с
полуосями можно представить в виде
таблицы
,
годограф Михайлова должен выглядеть
как на Рис.6, а пересечения годографа с
полуосями можно представить в виде
таблицы

|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
0 |
+ |
0 |
- |
0 |
РИС.6 Годограф Михайлова для АСР 5-го порядка
Таким
образом, можно наблюдать зигзагообразное
чередование нулей по строкам
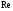 ,
,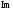 таблицы, а так же последовательную смену
положительных и отрицательных значений
координат.
таблицы, а так же последовательную смену
положительных и отрицательных значений
координат.
Именно это свойство и называется «чередованием корней».
Решение задач на определение устойчивости с помощью этого свойства сводится к проверке выполнения свойства перемежаемости нулей. Таким образом отпадает необходимость в построении всего годографа, достаточно только знать пересечения его с полуосями и последовательность этих пересечений.
Пример 1.
Определить устойчивость замкнутой АСР, если известны передаточные функции объекта и регулятора.
 ,
,

Решение.
Для
определения устойчивости методом
чередования корней необходимо определить
характеристический полином замкнутой
системы
 .
Для этого сначала нужно определить
передаточную функцию разомкнутой АСР
.
Для этого сначала нужно определить
передаточную функцию разомкнутой АСР

Находим характеристический полином замкнутой системы
 .
.
Выражение для годографа Михайлова
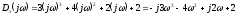
Для определения точек пересечения годографа с осями, выделяем действительную и мнимую части выражения
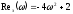

Теперь найдем последовательно точки пересечения с полуосями:
-годограф
пересекает действительную полуось
 ,
когда координата
,
когда координата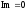 ,
поэтому из уравнения
,
поэтому из уравнения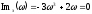 можно найти значения частот, при которых
годограф пересекает полуоси
можно найти значения частот, при которых
годограф пересекает полуоси ,
а затем и точки пересечения:
,
а затем и точки пересечения:
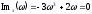
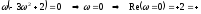
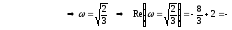
На самом деле достаточно знать только знак координаты пересечения, что само по себе определяет факт пересечения полуоси.
-годограф
пересекает мнимую полуось
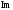 ,
когда координата
,
когда координата ,
поэтому из уравнения
,
поэтому из уравнения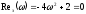 найдем значения частот, при которых
годограф пересекает полуоси
найдем значения частот, при которых
годограф пересекает полуоси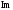 ,
и точки пересечения с ними:
,
и точки пересечения с ними:
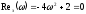
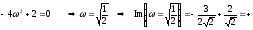 .
.
Теперь расположим найденные частоты в порядке возрастания
 .
.
Теперь заполним таблицу точками пересечения, соблюдая порядок возрастания частоты, и проверим выполнение условия чередования нулей. Кроме этого можно схематично изобразить прохождение годографа Михайлова на комплексной плоскости.
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
0 |
+ |
0 |
|
|
|
|
|
На
основании анализа заполнения таблицы
делается вывод об устойчивости замкнутой
АСР. 
Пример 2.
Определить устойчивость замкнутой АСР, если известны передаточные функции объекта и регулятора.
 ,
,
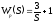
Решение.
Для
определения устойчивости методом
чередования корней необходимо определить
характеристический полином замкнутой
системы
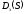 .
Для этого сначала нужно определить
передаточную функцию разомкнутой АСР
.
Для этого сначала нужно определить
передаточную функцию разомкнутой АСР
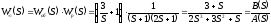
Находим характеристический полином замкнутой системы
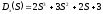 .
.
Выражение для годографа Михайлова
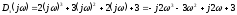
Для определения точек пересечения годографа с осями, выделяем действительную и мнимую части выражения


Теперь найдем последовательно точки пересечения с полуосями:
-годограф
пересекает действительную полуось
 ,
когда координата
,
когда координата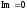 ,
поэтому из уравнения
,
поэтому из уравнения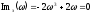 можно найти значения частот, при которых
годограф пересекает полуоси
можно найти значения частот, при которых
годограф пересекает полуоси ,
а затем и точки пересечения:
,
а затем и точки пересечения:

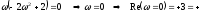

-годограф
пересекает мнимую полуось
 ,
когда координата
,
когда координата ,
поэтому из уравнения
,
поэтому из уравнения найдем значения частот, при которых
годограф пересекает полуоси
найдем значения частот, при которых
годограф пересекает полуоси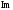 ,
и точки пересечения с ними:
,
и точки пересечения с ними:
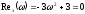
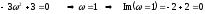 .
.
Располагая
найденные частоты в порядке возрастания,
мы видим, что годограф имеет не три
частоты пересечения, а две -
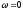 и
и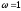 .
.
Заполним таблицу точками пересечения, соблюдая порядок возрастания частоты, и проверим выполнение условия чередования нулей.
|
|
|
|
|
|
|
+ |
0 |
|
|
|
0 |
0 |
|
Из
заполнения таблицы следует что годограф,
начинаясь на положительной вещественной
полуоси при 
 ,
проходит через точку начала координат,
что свидетельствует о нахождении
замкнутой АСР на границе устойчивости.
,
проходит через точку начала координат,
что свидетельствует о нахождении
замкнутой АСР на границе устойчивости.
