456

2.3. Метод Петрика

Метод Петрика позволяет исключить процедуру построения и анализа таблицы меток. После получения всех первичных импликант, для каждого минитерма строится дизъюнкция из тех импликант, которые входят в данный минитерм. Затем все дизъюнкции логически перемножаются, раскрываются скобки, выполняются все поглощения, т. е. получается некоторая ДНФ. При этом, каждая конъюнкция, входящая в ДНФ, соответствует одной из тупиковых ДНФ. Выбирается самая короткая, которая соответствует МДНФ.

Пример
				0	0	1	1		0 1	0	0
f x1, x2, x3, x4 x1 x						2 x	3 x4 V x1 x2 x3 x4 V
0 1		0	1		0 1		1	1	1	0	0	1
x1 x2 x3 x4				V x1 x2 x3 x					4 V x1 x2 x3 x4				V
1	0	1	1		1 1		0	0	1 1		0	1
x1 x		2 x3 x4		V x1 x2 x3 x					4 V x1 x2 x3 x4 .
Минитермы 4-го ранга
I		II			III
0100*	0011*			0111*
	0101*			1011*
	1001*			1101*
	1100*
Минитермы 3-го ранга
I		II
100*	0 11
010 *	011
	01 1

101* 10 1 1 01

110 *

Минитермы 2-го ранга

I 10 10

Простые импликанты

0 11, 011, 01 1, 10 1, 1 01, 10

31

Записываем дизъюнкции из простых импликант, которые для простоты

обозначим:	x		1x3x4 A
0 11
011	x		2x3x4 B
01 1	x	1x x									C
10 1	x							22x4			D
				x
	1									4
1 01	x							3x			E
					x
10	x1								3	4	F.
						x
	2

В минитермы входят импликанты:

0100 ~ F

0011 ~ A V B

0101 ~ C V F

1001 ~ D V E

1100 ~ F

0111 ~ A V C

1001 ~ B V D

1101 ~ E V F .

Записываем конъюнкцию из этих дизъюнкций и выполняем операции поглощения

A V AB A ; A A V B A .

и перемножаем скобки.

F A V B C V F D V E A V C B V D E V F

F A V B D V E A V C B V D F A V BC D V BE

ADF V ABEF V BCDF V BCEF .

Получили 4 тупиковых ДНФ

ADF : x1x3x 4 x1 x 2 x 4 ABEF: x1x3x 4 x 2 x3x 4 BCDF: x 2 x3x 4 x1x 2 x 4 BCEF: x 2 x3x 4 x1x 2 x 4

x 2 x3

x1 x3x 4 x 2 x3

x1 x 2 x 4 x 2 x3

x1 x3x 4 x 2 x3

Минимальной является первая, т. е. МДНФ имеет вид:

f x1, x2, x3, x4 x1 x3x4 V x1x 2 x4 V x2 x3 .

2.4. Метод Блека - Порецкого

32

Недостатком рассмотренных методов является то, что сокращенная ДНФ строится по СДНФ, которая при n = 5, 6 становится довольно громоздкой.

Например, если функция имеет следующий вид ДНФ:

fx1, x2 , x3, x4 , x5 x1x3x4x5 V x2x3x4x5 V x 1 ,

итребуется определить для нее МДНФ, нужно построить СДНФ, которая состоит из 18 минитермов.

Метод Блека - Порецкого позволяет строить Сокр. ДНФ не по СДНФ, а по произвольной ДНФ. Метод основан на следующей теореме.

Теорема

	f x , ..., x			Ax
Если в ДНФ функции			входят две конъюнкции вида			и Bxi ,
	1	n			i

то имеет место равенство:

P P V AB ,

(*)

где P – ДНФ функции f x1, ..., xn .

Для построения Сокр. Д НФ по произвольной ДНФ исходную ДНФ следует дополнить новыми членами по правилу (*), затем выполнить операцию поглощения, затем снова дополнить и снова выполнить поглощение и т. д., до тех пор, пока это возможно. Получив Сокр. ДНФ, можно воспользоваться дл я получения МДНФ методом Квайна - Мак - Класки или Петрика.

Пример

f x1, x2, x3 x1x2 V x2x3 V x1x2 x3 V x1x2 x3 .

Пары, удовлетворяющие теореме

x1x2 , x1x2 x3 , x1x2 , x1x2 x3 , x2x3, x1x2 x3 ,x2x3, x1x2 x3 , x1x2 x3, x1x2 x3 .

Дополняем исходную ДНФ

f x1, x2 , x3 x1x2 V x2x3 V x1x2 x3 V x1x2 x3 V V x1x3 V x2 x3 x1x2 V x2x3 V x2 x3 V x1x3 .

Здесь есть одна пара, удовлетворяющая условию теоремы x1 x 2 , V x2 x 3 ,

но она ничего не добавляет, т. е. мы получили Сокр. ДНФ. Далее по методу Квайна строим таблицу меток

33

	000	001	101	110	010
00-	1	1
-01		1	1
-10				1	1
0-0	1				1

Существенные импликанты -01, -10. Здесь две МДНФ

f(x1, x2 , x3) x 2 x3 x2 x 3 x 1 x 2

f(x1, x2 , x3) x 2 x3 x2 x 3 x 1 x 3

Замечание.

Проблема минимизации функций может быть сформулирована и решена в других базисах, например, , , / , . Для этих базисов разработаны методы

минимизации.

ЛИТЕРАТУРА

1. Мендельсон Э. Введение в математическую логику. – М. : Наука, 1984. 2. Марков А.А. Элементы математической логики. – М.: Изд -во МГУ, 1984.

3. Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику: учебное пособие. – М. : Изд -во Моск. ун-та, 1982.

4. Ершов Ю.Л., Палютин Е.А. Математическая логика: (Уч. пособие для ВУЗов). –

М.: Наука, 1979.

5. Новиков П.С. Элементы математической логики – М. : Наука,1973. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Упрощение логических выражений с помощью тождеств основывается на интуитивных решениях и представляет большие трудности, особенно при большом числе переменных. При этом бывает трудно оценить, является ли полученное выражение простейшим или возможны дальнейшие упрощения.

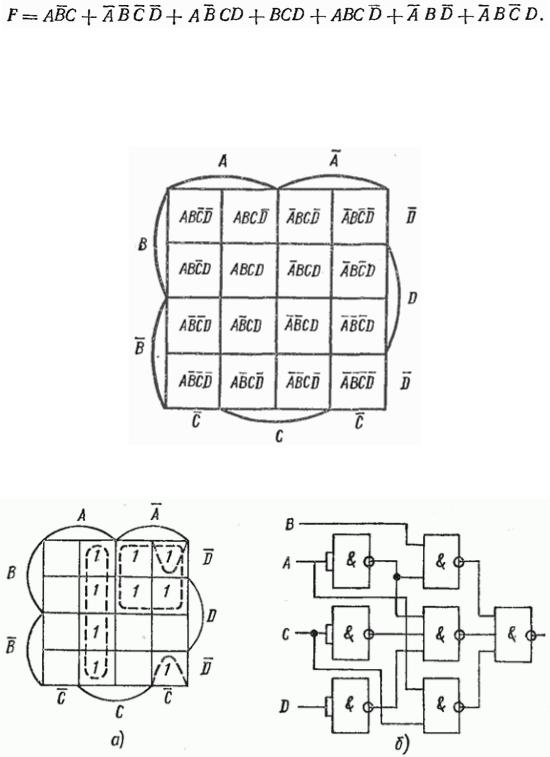
Минимизацию логических функций можно провести, используя диаграммы Вейча (или аналогичный метод карт Карно). Диаграмма Вейча для функции F четырех переменных А, В, С, D представлена на рис. 4.13. Каждая из переменных принимает два значения, т. е.

возможны комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях

диаграммы обозначены значения каждой переменной. Диаграмма состоит четырех строк и четырех столбцов.

Рассмотрим минимизацию логической функции на примере.

34

Дано: Упростить функцию .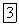

Решение разбиваем на четыре операции.

1.Преобразование исходного выражения. При преобразовании необходимо раскрыть скобки и исключить знаки инверсии над комбинацией переменных. Последнее осуществляется с помощью формул де Моргана. Получим

2.Заполнение диаграммы Вейча проводим при наличии в полученном выражении соответствующих комбинаций входных переменных, эти клетки обозначаются знаком 1 (рис. 4.14,а). Если слагаемое не содержит одного или нескольких переменных, то должны заполняться клетки, соответствующие и прямому, и инверсному значениям отсутствующей переменной.

Рис. 4.13. Диаграмма Вейча для функции четырех переменных

Рис. 4.14. К минимизации схемы логического комбинационного устройства: а — диаграмма Вейча; б — схема на элементах

35

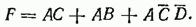
Например: 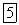. Заполняются клетки ABCD и ABCD.

3. Производится «склейка» клеток. Можно склеить (т. е. объединить, лак показано на рис. 4.14, я) целую заполненную строку, целый столбец, полстроки или полстолбца. Можно склеить соседние строки, столбцы, полустроки и полустолбцы. Склейки можно располагать через границы диаграммы Вейча, т. е. объединяя нижиий и верхний, правый и левый края. Одиа склейка может накладываться на другую. Склейки содержат 2, 4, 8 клеток.

Для успешной минимизации нужно расположить на таблице минимальное количество склеек, каждая из которых содержит наибольшее количество клеток.

Склейки для логической функции F показаны на рис. 4.14, а.

4. Расшифровка склеек. Каждая склейка представлена в виде конъюнкции переменных. Второй столбец на диаграмме рис. 4.14, я расшифровывается как АС, так как он охватывает и прямые, и инверсные значения переменных В и D, т. е. от В до D не зависит. Склейка в правой верхней части таблицы расшифровывается как АВ, а склейка из двух клеток в четвертом столбце соответствует ACD. Результат минимизации:

На рис. приведена схема на элементах , реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.

Процедура минимизации функций с помощью диаграмм Вейча очень проста, и ее использование заменяет путь сложных преобразований с помощью тождеств. С помощью

диаграмм Вейча можно минимизировать и функции трех переменных, при этом , т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.

Правила склеек не изменяются. Диаграмма Вейча функции двух переменных содержит четыре клетки.

Основы синтеза цифровых устройств

2.1 Последовательность операций при синтезе цифровых устройств комбинационного типа

1 Составление таблицы истинности комбинационного цифрового устройства (КЦУ) согласно его определения, назначения, словесного описания принципа работы.

2 Составление логической формулы согласно таблицы истинности.

3 Анализ полученной формулы с целью построения различных вариантов и нахождения наилучшего из них по тем или иным критериям.

4 Составление функциональной схемы КЦУ из элементов И, ИЛИ, НЕ.

2.2 Аналитическая запись логической формулы КЦУ

Запись в форме СДНФ (Совершенная дизъюнктивная нормальная форма).

В СДНФ логическая формула представляет собой логическую сумму нескольких логических произведений, в каждое из которых входят все независимые переменные с отрицанием или без него.

36

Формула получается в два этапа:

а) Записывается логическая сумма произведений, в каждое из которых входят все независимые переменные. Количество слагаемых равно числу наборов таблицы истинности, на которых логическая функция равна «1»;

б) ставится знак инверсии над теми независимыми переменными, которые равны «0» в рассматриваемом наборе.

Запись в форме СКНФ (Совершенная конъюнктивная нормальная форма).

В СКНФ формула представляет собой логическое произведение нескольких логических сумм, в каждую из которых все независимые переменные с отрицанием или без него.

Как и в предыдущем случае, формула получается в два этапа:

а) Записывается логическое произведение всех сомножителей; количество сомножителей равно числу наборов таблицы истинности, на которых логическая функция равна «0»;

б) ставится знак инверсии над теми независимыми переменными, которые равны «1» в рассматриваемом наборе.

Структурные формулы в виде СДНФ и СКНФ эквивалентны и, с помощью законов алгебры, логики могут быть преобразованы одна в другую.

Пример: Синтезировать мажоритарный логический элемент на три входа.

Мажоритарным называется логический элемент, выходное состояние которого совпадает с большинством входных сигналов.

На основании данного словесного описания мажоритарного элемента составлена его таблица истинности (Таблица 5).

Таблица 5 - Таблица истинности мажоритарного элемента

X1 X2 X3 Y

0 0 0 0

0 0 1 0

0 1 0 0

0 1 1 1

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 1

На основе таблицы истинности записывается СДНФ или СКНФ функции, а затем составляется функциональная схема элемента.

СДНФ: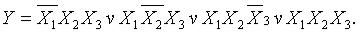

37

СКНФ: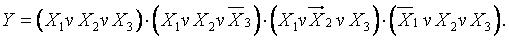

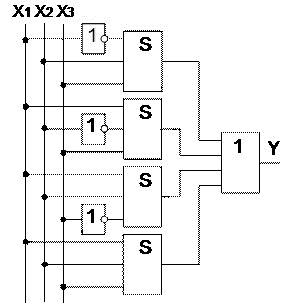
Рисунок 3 Функциональная схема мажоритарного элемента

Функциональная схема элемента, составленная на основе функции СДНФ мажоритарного элемента, приведена на рисунке 3. Схема состоит из 8 элементов, имеющих общее количество входов 19. Количество входов характеризует сложность схемы и называется «Число по Квайну». Схема составленная на основе функции СКНФ, также будет иметь 19 входов.

2.3 Понятие базиса

Любая, сколь угодно сложная логическая функция, представленная таблицей истинности, может быть представлена в форме СДНФ или СКНФ. Каждая из этих формул записана с помощью логического сложения, умножения и отрицания. Поэтому для реализации логических устройств, предназначенных для обработки цифровых сигналов, в общем случае необходимо иметь элементы, выполняющие операции И, ИЛИ, НЕ. Такой набор элементов называется функционально полной системой логических элементов или логическим базисом. Это означает, что из комбинации логических элементов И, ИЛИ, НЕ, взятых в

достаточном количестве, можно построить сколь угодно сложное цифровое устройство. Базис из элементов: И, ИЛИ, НЕ называется основным.

Однако, число необходимых элементов в такой системе можно уменьшить, исключив из неё либо элемент ИЛИ, либо элемент И. Например, в соответствии с теоремой де Моргана,

имеем 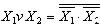. Отсюда следует, что операцию логического ИЛИ можно заменить операцией И над инверсными значениями переменных, , а затем к результату применить операцию инверсии и тем самым исключить элемент ИЛИ (Рисунок 4).

38

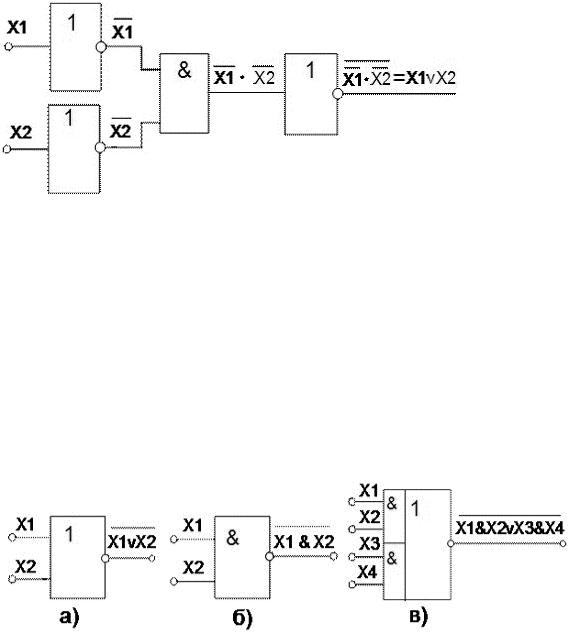
Рисунок 4 Реализация элемента ИЛИ на элементах НЕ, И

Аналогично можно исключить элемент И, заменив его операцией логической суммы над инверсными значениями переменных с последующим применением операции

инверсии 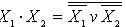Следовательно, системы, состоящие из двух элементов(ИЛИ, НЕ либо И, НЕ), также являются функционально полными системами и содержат минимальный логический базис.

При схемной реализации функционально полных систем с минимальным логическим базисом идут по пути использования универсальных логических элементов: ИЛИ-НЕ, И-НЕ и И-ИЛИ- НЕ (Рисунок 5).

Рисунок 5 Универсальные логические элементы

Элемент ИЛИ-НЕ Рисунок 5,а) осуществляет логическую операцию 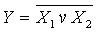, называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую

операцию и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в)

осуществляет операцию 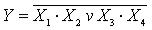и является элементом сложного базиса.

Элементы универсальных базисов позволяют реализовать все три основные логические операции (Рисунок 6). Например, для осуществления операции НЕ с помощью элемента И-НЕ

достаточно объединить входы 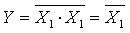(рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.

39

Рисунок 6 Реализация функций НЕ, И и ИЛИ на элементах И-НЕ

При последовательном соединении элемента И-НЕ и инвертора осуществляется операция логического умножения: 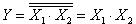(рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения: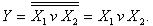

Применение трёх элементов И-НЕ, два из которых работают в режиме инвертирования с объединёнными входами (рисунок 6,в), позволяют реализовать операцию логического

сложения 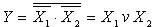. Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения

В общем случае логическая функция Y может зависеть от нескольких переменных X1,X2,…,Xn. Говорят, что функция Y определена, если известны её значения для всех возможных наборов переменных. Функция Y не определена, когда некоторые сочетания переменных по условию задачи невозможны. В этом случае её можно доопределить, приписав ей значение «1» либо «0» по соображениям удобства реализации.

2.4 Минимизация логических формул

Однозначная зависимость сложности логической формулы и функциональной схемы логического устройства приводят к выводу необходимости минимизации структурной формулы логического устройства. Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики.

2.4.1 Расчётный метод минимизации

Применение этого метода состоит в последовательном применении к некоторой формуле законов и правил тождественных преобразований алгебры логики. При этом широко используют следующие приёмы: прибавление одного или нескольких членов, входящих в

СДНФ, поскольку X X X = X; выделение членов, содержащих множитель 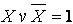; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм.

Пример: Минимизировать функцию СДНФ мажоритарного элемента (См. п.2.2) и реализовать его схему на элементах основного базиса.

40