Курс лекций по ТМО_ Абузова Ф[1].Ф

Функцию qx+dx разложим в ряд Тейлора:

q		=q		+	∂qx dx +	∂2qx	dx2	+...	(1.13)
	x+dx
			x		∂x	∂x2 2!

Возьмём два первых члена разложения и подставим в выражение

для dQx1 :

		∂q	x		∂q	x
dQx1 = qx	dy dz dτ − qx +						dx dy dz dτ . (1.14)
				dx dy dz dτ =−
		∂x			∂x

Аналогично находят выражения и по другим осям.

dQ

=−

∂qy

dx dy dz dτ ;

(1.15)

y1

∂y

dQ

=−

∂qz

dx dy dz dτ .

(1.16)

z1

∂z

Таким образом, получаем

∂qx

∂qy

=−

∂qz

dQ =dQ

+dQ +dQ

+

+

dx dy dz dτ .

(1.17)

∂x

∂y

1

x1

y1

z1

∂z

2. Определим dQ2 .

Пусть qv – мощность внутренних источников теплоты, т.е. количество

теплоты, выделяемое внутренними источниками в единице объёма среды

в единицу времени.

[qv] = Вт/м3.

Получаем

dQ2 = qv dv dτ = qv dx dy dz dτ .

(1.18)

3.Определим dQ .

Результат зависит от характера термодинамического процесса.

∙ Изохорный процесс

dQ = dU,

(1.19)

где U = f (x,y,z,τ) – внутренняя энергия тела.

dU = c′

∂t

dτ dv = c

ρ

∂t

dτ dv =c

ρ

∂t

dx dy dz dτ ,

(1.20)

∂τ

v

v

∂τ

v

∂τ

13

где c′	– изохорная теплоёмкость единицы объёма, Дж/(м3·К);
v
cv	– изохорная теплоёмкость единицы массы, Дж/кг·К;
ρ – плотность, кг/м3.
Между приведёнными выше величинами существует соотношение
	с′v =ρ cv .	(1.21)

Подставим значения в общее уравнение:

cρ ∂t

v ∂τ

dQ1 +dQ2 =dQ = dU;

	∂qx		∂qy		∂qz
dx dy dz dτ =−		+		+		dx dy dz dτ +
	∂x		∂y
					∂z

+qv dx dy dz dτ .

(1.22)

(1.23)

В итоге имеем

			∂t
	c	ρ		=−div q +q	.	(1.24)
			∂τ
	v			v

Полученное выражение – дифференциальное уравнение энергии для изохорного процесса переноса теплоты.

∙ Изобарный процесс

dQ = dH,

(1.25)

где H = f (x,y,z,τ) – энтальпия тела.

dH = c′

∂t

dτ dv = c

ρ

∂t

dτ dv =c

ρ

∂t

dx dy dz dτ ,

(1.26)

∂τ

p

p

∂τ

p

∂τ

где cp′ – изобарная теплоёмкость единицы объёма, Дж/м3·К; cp – изохорная теплоёмкость единицы массы, Дж/кг·К.

Заметим, что

	c			∂t	=	∂(cp t)		=	∂h	.	(1.27)
		p		∂τ		∂τ			∂τ
Тогда после замены получаем
dQ = ρ	∂h dτ dv =ρ						∂h dx dy dz dτ .				(1.28)
	∂τ						∂τ

Подставим значения в общее уравнение:

14

		dQ1 +dQ2 =dQ = dH;								(1.29)
	∂h			∂qx		∂qy
								∂qz
ρ		dx dy dz dτ =−			+		+			dx dy dz dτ +
	∂τ			∂x		∂y		∂z		(1.30)
		+qv		dx dy dz dτ .
В итоге имеем
		ρ	∂h =−div q +qv .							(1.31)
			∂τ

Полученное выражение – дифференциальное уравнение энергии

для изобарного процесса переноса теплоты.

В твёрдых телах перенос теплоты осуществляется в соответствии с законом Фурье, при этом cp ≈ cv . Примем, что cp =cv =c .

Проекция вектора плотности теплового потока на соответствующие

оси:

qx	=−λ		∂t		;	(1.32)
			∂x
qy	=−λ		∂t	;		(1.33)
			∂y
qz	=−λ		∂t	.		(1.34)
			∂z

После подстановки в дифференциальное уравнение энергии для пе-

реноса теплоты получаем:

∂t

∂

∂t

∂

∂

∂t

∂t

c ρ

=

λ

+

λ

+

λ

+qv ;

(1.35)

τ

x

y

∂

∂

x

∂

∂y

∂z

∂

z

∂

∂t

1

div(λ grad t)+

qv

=

.

(1.36)

∂τ

c ρ

c ρ

Полученное выражение – общее уравнение теплопроводности.

Считаем, что теплоёмкость с, плотность ρ и коэффициент теплопро-

водности λ – постоянные величины.

div(grad t)=	∂2t		∂2t		∂2t	2
		+		+		=	t .	(1.37)
	∂x2		∂y2		∂z2

15

Тогда

∂t

=

λ

2t +

qv

.

(1.38)

∂τ c ρ

c ρ

Окончательно

∂t

= a 2t +

qv

,

(1.39)

∂τ

c ρ

где a =

λ

– коэффициент температуропроводности, м2/с.

c ρ

Коэффициент температуропроводности a характеризует скорость выравнивания температур в неравномерно нагретом теле при нестацио-

нарном режиме. Он зависит от природы вещества и у жидкостей и газов он меньше, чем у твёрдых тел.

Возможны следующие частные случаи общего уравнения теплопро-

водности:

Поле

Есть внутренние

Нет внутренних

температур

источники теплоты, qv ≠0

источников теплоты, qv =0

∂t

2

qv

= a

t +

∂t

= a 2t

Нестационарное

∂τ

c ρ

общее уравнение

∂τ

уравнение Фурье

теплопроводности

∂2t

+

∂2t

+

∂2t

+

qv

=0

∂2t

+

∂2t

+

∂2t

=0

Стационарное

∂y2

∂z2

∂x2

λ

∂x2

∂y2

∂z2

уравнение Пуассона

уравнение Лапласа

Лекция 2

Условия однозначности для процессов теплопроводности

Число различных единичных явлений теплопроводности, описывае-

мых дифференциальным уравнением (1.39), неограниченно велико, это уравнение имеет бесчисленное множество решений. Для выделения нуж-

ного решения при описании конкретного процесса необходимо уравнение

(1.39) дополнить условиями однозначности.

Условия однозначности включают:

16

∙Временные – определяют значения переменных в начальный и конечный моменты времени.

∙Геометрические – характеризуют форму и размеры тела.

∙Физические – задают зависимости теплофизических парамет-

ров, входящих в уравнение, и закон распределения внутренних источников теплоты.

∙Граничные – характеризуют взаимодействие рассматриваемо-

го тела с окружающей средой:

o I рода – задано распределение температуры на поверх-

ности тела (частный случай, когда tс =const ).

oII рода – задано распределение плотности теплового по-

тока на поверхности тела qï = f (x,y,z,τ) .

o III рода – задана температура окружающей среды t ж и

закон теплообмена между телом и окружающей средой.

Для описания процесса теплообмена между поверхностью тела и ок-

ружающей средой используется закон Ньютона-Рихмана (гипотеза):

q =α (tс −tж ),

(2.1)

где α – коэффициент теплоотдачи, который не является теплофизиче-

ским параметром, а рассчитывается.

Коэффициент теплоотдачи α характеризует интенсивность тепло-

отдачи между поверхностью и омывающей её жидкостью (газом).

α = Вт/(м2·град).

Если в теле нет внутренних источников теплоты (qv =0 ), то измене-

ние температуры во времени пропорционально изменению перепада тем-

ператур в пространстве.

Дифференциальное уравнение и условия однозначности – единст-

венный способ определения конкретной задачи.

17

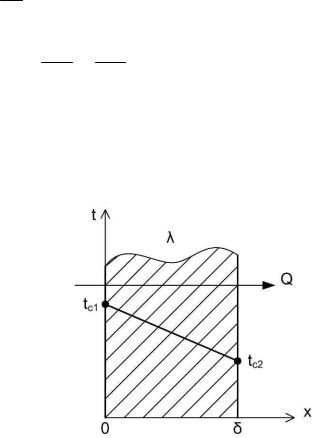
1.3.1. Теплопроводность при стационарном тепловом режиме (граничные условия I рода)

Плоская стенка, qv =0

Запишем условия однозначности:

∂t

1. Временные: ∂τ =0 .

∂2t ∂2t

2.Геометрические: ∂y2 = ∂z2 =0 , толщина стенки равна δ .

3.Физические: λ =const , стенка однородна.

4.Граничные – I рода: известны температуры на поверхностях стенки: tc1

иtc2 .

Рис. 2.1. Плоская однородная стенка

Таким образом, уравнение теплопроводности принимает следующий

вид:

	d2t	=0 .	(2.2)
	dx2

Решение:

		dt	=C ;	(2.3)
		dx	1
	dt =C1 dx ;
	t =C1 x +C2 .			(2.4)
При x =0	t = tc1 ;
			18

tc1 =C1 0 +C2 ;

C2 = tc1.

(2.5)

При x = δ

t = tc2 ;

tc2 =C1 δ +tc1 ;

C

=

tc2 −tc1

.

2.6)

1

δ

Получаем

t =

tc2 −tc1

x +t

=−

tc1 −tc 2

+t

.

(2.7)

c1

c1

δ

δ

Таким образом, распределение температуры в плоской однородной стенке имеет вид

	t = t		−	tc1 −tc2	x .	(2.8)
		c1		δ

Найдем выражение для поверхностной плотности теплового потока:

	dt		=−	tc1 −tc2					;		(2.9)
	dx					δ
		q =−λ				dt		;
						dx
q = λ		tc1 −tc2			=		tc1 −tc2			.	(2.11)

δδ λ

Выражение δ – термическое сопротивление теплопроводности

λ

для однородной стенки:

Rλ

=

δ

.

(2.12)

λ

[Rλ] = (м·град)/Вт .

Тепловой поток сквозь стенку:

Q =

tc1 −tc2

F =

tc1 −tc2

.

(2.13)

δ λ

δ

λ F

Иногда термическое сопротивление находят как Rλ

=

δ

.

λ F

19

Количество теплоты, прошедшее через стенку за время τ, определя-

ется

	Q =	tc1 −tc2	τ .	(2.14)
		δ

λ F

Многослойная плоская стенка

Рис. 2.2. Многослойная стенка

Из (2.13) имеем

t

−t

=

Q δ1

.

(2.15)

c1

c2

λ1 F

По закону сохранения

энергии Q = const ,

т.к. стенка плоская

F = const .

t

−t

=

Q δ2

;

(2.16)

c2

c3

λ2 F

t

−t

=

Q δ3

.

(2.17)

c3

c 4

λ3 F

Если сложить (2.15) – (2.17), получаем

		Q		λ		λ	2		λ
				1					3
tc1 −tc4	=				+			+		.	(2.18)
		F		δ		δ			δ
							2
				1					3

В общем случае для стенки, состоящей из n слоёв, имеем

20

			Q	n	δi
	tc1 −tcn+1	=		∑		.	(2.19)
			F	i=1	λi

Распределение температур внутри слоя определяется по формуле

(2.8), а на поверхности между слоями:

				Q	n	δi
	tcn+1	= tc1	−		∑		.	(2.20)
				F	i=1	λi

Тепловой поток через многослойную стенку определяется :

Q =		tc1 −tcn+1							.		(2.21)
			1	n		δi
				∑
			F			λi
				i=1
Поверхностная плотность теплового потока через многослойную
стенку:
q =		tc1 −tcn+1								.	(2.22)
				n	δi
			∑
					λi
				i=1

Термическое сопротивление теплопроводности многослойной стенки:

			1	n	δi
	RλΣ	=		∑		.	(2.23)
			F	i=1	λi

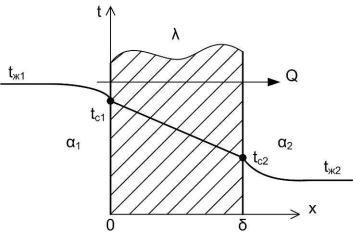
1.3.2. Теплопередача (теплопроводность при граничных условиях III рода)

Плоская однородная и многослойная стенки

Рис. 2.3. Плоская однородная стенка при граничных условиях III рода:

21

На рис. 2.3 α1 – коэффициент внутренней теплоотдачи,

фициент внешней теплоотдачи.

Заданы tж1 и tж2 , по закону Ньютона-Рихмана имеем:

q =α1 (tж1 −tc1);

q =α2 (tc1 −tж2 ).

По (2.11)

q = tc1 −tc2 .

δλ

Из (2.24) – (2.26) получаем:

α2 – коэф-

(2.24)

(2.25)

(2.26)

tж1 −tc1

=

q

;

(2.27)

α1

tc1 −tc2

=q

δ

;

(2.28)

λ

t

−t

=

q

.

(2.29)

c2

ж 2

α2

Складывая (2.27) – (2.29) имеем

		1		δ		1
tж1 −tж2	= q		+		+		.	(2.30)
				λ		α2
	α1

Поверхностная плотность теплового потока

q =		tж1 −tж2						.	(2.31)
		1	+	δ	+	1

α1 λ α2

Коэффициент теплопередачи для однослойной стенки

k =	1
	1 + δ + 1 .	(2.32)

α1 λ α2

Коэффициент теплопередачи k не является теплофизическим па-

раметром, а рассчитывается; он характеризует интенсивность теплопере-

дачи от одной жидкости (газа) к другой через разделяющую их стенку.

22