с инета для метод

Гл.4. Диэлектрики в электростатическом поле	131

Разность потенциалов между обклад-

+σ

ками уменьшилась и стала равной

– – – – – – – – – – – – – –

–σ′

ϕ =

d

1

+

E

1

0

ε

ε

2

2

+σ′

вместо первоначальной Δφ0 = Е0d, где

+ + + + + + + + + + + + +

d – расстояние между пластинами

1

–σ

а)

конденсатора. Такой результат связан

с тем, что электрическое поле втягива-

σ1

σ2

ет диэлектрик внутрь конденсатора и

–σ′

совершает работу, что приводит к

– – – – – – –

– – – – – – –

уменьшению потенциальной энергии

2

1

ε

системы, пропорциональной разности

потенциалов. Подробно

этот вопрос

+ + + + + + +

+σ′

будет рассмотрен в следующей главе.

–σ1

–σ2

В случае б)

произойдет перерас-

б)

пределение сторонних зарядов на пла-

Рис. 4.10.

Конденсаторы,

час-

стинах конденсатора так, чтобы на-

тично заполненные

диэлектри-

пряженность поля в воздушном про-

ками (задача 4.3.11)

межутке и в диэлектрике стала одина-

ковой: Е1 = Е2 = Е. К этому выводу можно прийти, рассматривая разность потенциалов между пластинами, которая равна Δφ = Еd независимо от пути перехода от одной пластины к другой – через воздушный промежуток или через диэлектрик. В обозначениях

рис. 4.10б.

E =	σ1 =	σ2 − σ′	=	σ2	.
	ε0	ε0		εε0

Отсюда получаем, что ε σ1 = σ2. По условию, диэлектрик заполняет половину объема конденсатора. Поэтому по закону сохранения за-

ряда исходная

плотность

σ = ε E =

σ1 + σ2

. Таким образом,

0

0

2

σ =

2ε0E0

, а E =

2E0

. Следовательно,

1

ε +1

ε +1

D =

2

ε

E и D =

2ε

ε

E

.

1

ε +1

0 0

2

ε +1

0

0

2

Разность потенциалов здесь равна Δφ = Ed = ε +1E0d ; она меньше, чем была первоначально. Как и в предыдущем случае, в

132	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

процессе заполнения конденсатора диэлектриком электрические силы совершают работу, и потенциальная энергия системы уменьшается.

Ответ: а) Е1

= Е0, E2 =

E0

;

D1 = D2 = ε0Е0;

ε

б) Е1

= Е2 =

2E0

; D =

2

ε E ,

D =

2ε

ε

E

.

ε +1

1

ε +1 0 0

2

ε +1 0

0

Задача 4.3.12. Решить предыдущую задачу, считая, что конденсатор с самого начала подключен к источнику ЭДС и разность потенциалов между обкладками не меняется.

Решение

Разность потенциалов между обкладками вначале равна Δφ = Е0d и в дальнейшем не меняется. В случае а) после внесения диэлектрика в конденсатор напряженность поля в диэлектрике Е2 будет в ε раз меньше напряженности Е1 поля в воздушном проме-

	жутке: E2 =	E1	. Если выразить Δφ через Е1 и Е2, то получим:
		ε
					d		(E + E					)= E			d				1
			Δφ =														1+				.
																			ε
					2		1				2			1	2
	Учитывая неизменность Δφ, находим отсюда
			E =				2ε	E		,		E		=			2	E			.
			1			ε +1			0				2			ε +1				0

Из определения вектора D получаем

2ε

D1 = D2 = ε +1ε0E0 .

В случае б) напряженности Е1 и Е2 одинаковы (как и в предыдущей задаче). Из постоянства Δφ сразу следует вывод: Е1 = Е2 = Е0. Следовательно, D1 = ε0Е0 и D2 = ε0ε Е0.

Ответ: а) E =

2ε

E

,

E

=

2

E

, D1 = D2 =

2ε

ε

E

.

1

ε +1

0

2

ε +1

0

ε +1 0

0

б) Е1 = Е2 = Е0, D1 = ε0Е0, D2 = ε0ε Е0.

Задача 4.3.13. Сферический конденсатор наполовину заполнен жидким диэлектриком с проницаемостью ε = 7 (рис. 4.11). Радиусы

Гл.4. Диэлектрики в электростатическом поле	133

поверхностей: внутренней R1 = 5 см, внешней R2 = 6 см. Определить емкость конденсатора, пренебрегая искривлением линий поля на границе диэлектрика.

ϕ1				ϕ2
	С1
	С2

ε

Рис. 4.11. Сферический конденсатор,	Рис. 4.12. Эквивалентная схема к задаче
частично заполненный жидким диэлек-	4.3.13
триком (задача 4.3.13)

Решение

Обкладки конденсатора являются эквипотенциальными поверхностями, поэтому конденсатор можно рассматривать как систему двух параллельно включенных конденсаторов (рис. 4.12), у которых одна пара обкладок имеет потенциал φ1 внешней поверхности рассматриваемого сферического конденсатора, а вторая пара

– потенциал внутренней поверхности φ2. Так как диэлектрик заполняет сферический конденсатор наполовину, емкости C1 и C2 равны (гл. 3, (3.9))

	C1 =	2πε0R1R2			, C2 = εC1
			R2 − R1
соответственно. Отсюда получаем:
	C = C1+ C2 =			2πε0R1R2			(ε +1) .
				R2 − R1
Ответ:	C =		2πε0R1R2			(ε +1) .
			R2 − R1

Задачи типа 4.4

Определение напряженности поля внутри и вне диэлектрика с заданным статическим состоянием поляризации

Метод решения: Использование формул (4.1) и (4.2) для определения плотности связанных зарядов и затем расчет как в задачах типа 4.2.2.

134	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Задача 4.3.14. Пластинка из электрета толщины h помещена внутри плоского воздушного конденсатора, обкладки которого соединены между собой. Поляризованность пластинки P направлена по нормали к ее плоскости. Определить напряженность и индукцию электрического поля внутри и вне пластинки. Расстояние между обкладками конденсатора равно d.

Решение

На поверхностях пластинки существуют связанные заряды с плотностью σ′ = ±Р (рис. 4.13). За счет электростатической индукции на обкладках конденсатора появляются заряды противополож-

ных знаков с некоторой плот-
ностью σ. Известно, что на					–σ
поляризованность	электрета			E1			+σ′
внешнее поле влияет слабо,		+ + + + + + + + + + + +
											d
									h
поэтому изменением P за счет						P
				E2
поля индуцированных зарядов							-σ′
			– – – – – – – – – – – – –
можно пренебречь. Идея ре-
					+σ
шения задачи состоит в том,		Рис. 4.13. Система, состоящая из конден-
что потенциалы	обкладок	сатора и пластинки из электрета (задача
конденсатора равны. Это дает		4.3.14)
уравнение

E1(d – h) + E2h = 0.

где E1 – напряженность поля вне пластины ( E1 = σε0 ), E2 – внутри ( E2 = (σ − σ′)ε0 ). С учетом направлений напряженностей и равенства σ′ = Р находим:

E1(d – h) + (E −

P

)h = 0.

1

ε

0

откуда E =

P

h

. Следовательно, E

= −

P

d − h

.

1

ε

0

d

2

ε

0

d

Теперь легко найти величину плотности индуцированных на об-

кладках конденсатора зарядов: σ = ±P h , положительный заряд – d

на нижней обкладке, отрицательный – на верхней. Внутри конденсатора свободные заряды отсутствуют, поэтому линии вектора D непрерывно проходят от нижней обкладки до верхней обкладки параллельно вектору P. Вектор D1 в воздушном промежутке нахо-

Гл.4. Диэлектрики в электростатическом поле	135

дим из (4.6) D1 = ε0E1 = P h . Для вектора D2 в электрете соотноше- d

ние (4.6) неприменимо, поэтому нужно использовать общее определение (4.5)

D2 = ε0E2 + P = P h . d

Разумеется, D1 = D2 из условия непрерывности нормальной компоненты вектора индукции на границе диэлектрика.

Ответ: вне пластинки: E =					P			h	;
	1				ε	0		d
внутри: E2 = −	P		d − h	; D1 = D2				= P		h	.
	ε0 d									d

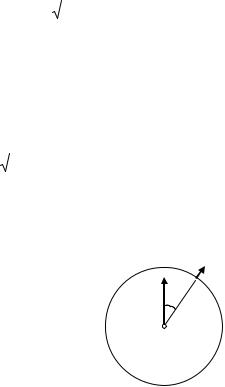
Задача 4.3.15 (базовая задача). Найти напряженность электрического поля в центре прямого круглого цилиндра длиной h и радиусом R, поляризованность которого параллельна его оси, однородна и равна Р (рис. 4.14).

Решение

Из условия однородной поляри-

зованности		следует, что		плотность		E	P
					–σ′
объемных связанных зарядов внутри							O	+σ′ x
цилиндра равна нулю. На торцах ци-
линдра находятся			противоположные
по	знаку	поверхностные		связанные	Рис. 4.14. Векторы напряженно-
заряды, распределенные равномерно с					сти поля Е и поляризованности
плотностью σ′ = ±Р. Таким образом,					Р на оси однородно поляризо-
напряженность поля в центре цилин-					ванного	цилиндра		(задача
дра	равна	сумме	напряженностей,		4.3.15)

создаваемых двумя противоположно заряженными дисками на их общей оси. Напряженность на оси диска вычислена в задаче 1.3.6 (глава 1) и равна

	σ						x
Е =		1	−							,
	2ε0				x	2	+ R	2

где R – радиус диска, а х – расстояние вдоль оси до плоскости диска. В нашем случае х = h/2, откуда получаем ответ:

Рис. 4.15. Распределение связанных зарядов на боковой поверхности однородно поляризованного цилиндра (задача 4.3.16)

136	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
		P						h
	E = −		1	−							.
						h	2	+ 4R	2
		ε0

Поляризованный цилиндр можно представить себе как результат малого сдвига всех положительных зарядов относительно всех его отрицательных зарядов. Видим, что вектор напряженности поля Е, создаваемой поляризованностью Р, направлен противоположно вектору Р. Поэтому поле от связанных зарядов часто называют деполяризующим полем.

	P						h
Ответ: E = −		1	−							.
					h	2	+ 4R	2
	ε0

Задача 4.3.16. Поляризованность Р в предыдущей задаче направлена перпендикулярно оси цилиндра. Найти напряженность поля в центре цилиндра.

Решение

Из условия задачи следует, что связанные заряды возникнут только на боковой поверхности цилиндра. Плотность связанных зарядов определяется формулой (4.2) и равна σ′ = (Pn) = Pcos φ, где φ – азимутальный угол, а n – единичный вектор нормали к поверхности цилиндра (рис. 4.15).

+σ′ + + + n

++

+

P ϕ

+

O

––

–			–
–σ′	–	–	–

Для вычисления напряженности в центре цилиндра надо пред-

ставить боковую поверхность цилиндра в виде последовательности бесконечно узких колец с зарядом, распределенным на них с линейной плотностью dτ = σ′dx, и воспользоваться результатом решения задачи 1.3.21 (глава 1), где вычислена напряженность поля на оси такого кольца:

dE =	dτ					,
			x2		3/2
	4ε0R 1	+
			R	2

Гл.4. Диэлектрики в электростатическом поле	137

	где х – расстояние от плоско-			dx
	сти кольца до точки наблю-
	дения О (в нашем случае это
	центр цилиндра		(рис. 4.16)).	O x
	Полную напряженность поля			x
	в центре цилиндра найдем,
	интегрируя	это	выражение
	по всем х от – h/2 до + h/2.			Рис. 4.16. К вычислению напряженности
	Как и в предыдущей задаче,			электрического поля в центре однородно
	направление вектора Е про-			поляризованного цилиндра (задача 4.3.16)
	тивоположно	направлению

вектора Р. С учетом этого обстоятельства получаем

Ph

Е = − .

2ε0 h2 + 4R2

Если цилиндр очень длинный (h → ∞), то напряженность поля

P

внутри него будет однородной и равной E = − 2ε0 .

Ph

Ответ: Е= − .

2ε0 h2 + 4R2

Задача 4.3.17 (базовая задача). Диэлектрический шар поляризован однородно с вектором поляризации Р. Найти напряженность электрического поля внутри шара.

Решение

Из (4.2) следует, что на шаре имеются поверхностные заряды, плотность которых σ′ = (Pn) = Pcosϑ, где ϑ – полярный угол относительно вектора Р, а n – единичный вектор нормали к поверхности шара.

Данная задача легко сводится к ранее рассмотренной в главе 1 задаче 1.3.17. Указанную выше плотность поверхностных зарядов можно смоделировать следующим образом. Возьмем два шара, однородно заряженных одинаковой по величине объемной плотностью заряда ρ, но противоположного знака.

Сместим центр отрицательно заряженного шара O' относительно центра положительного шара O на малый вектор а против направления Р (рис. 1.17). Тогда внутри области пересечения ша-

138	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
ров получится суммарная нулевая						z
плотность заряда, а толщина по-					+	+ +		+ h
верхностного		слоя	некомпенси-
					+			+
рованного заряда в первом при-
					+		ϑ	+
ближении		будет		равна
						O
h(ϑ) = acosϑ,		что	эквивалентно		P		a	P
поверхностной плотности заряда						O'			y
σ = ρh(ϑ) = ρa cosϑ.			Очевидно,		–			–
что для получения			приведенной
					–			–
выше плотности поверхностного					–	–	–	–
заряда	нужно	положить		Р = ρa,	Рис. 1.17.	К вычислению			напря-
или в	векторном		виде	Р = –ρa.
При а → 0 данная			система по		женности поля		внутри однородно
					поляризованного			шара	(задача
распределению поляризационных					4.3.17)

зарядов эквивалентна нашей задаче.

В задаче 1.3.17 было найдено электрическое поле в области пересечения двух шаров, равномерно заряженных равной по модулю, но противоположной по знаку плотностью зарядов ±ρ, центры которых смещены относительно друг друга на вектор а. Было получено, что силовые линии этого поля параллельны а, его напряжен-

	ность E =	ρ	a . Используя это, можно сразу написать ответ для
		3ε0
	данной задачи E = −			1		P .
				3ε	0

1

Ответ: E = − 3ε0 P .

Замечание: электрическое поле, порожденное поляризацией материала тела, называется деполяризующим. При однородной поляризации тела это поле будет однородным только для тел в форме эллипсоида или его частных случаев – шара или сфероида. Для эллипсоида E = − NˆP , где Nˆ – тензор деполяризации формы. В главных осях эллипсоида тензор Nˆ диагонален и сумма диагональных элементов всегда равна 1. Поэтому в шаре все коэффициенты деполяризации равны 13, что и было получено в данной задаче.

Аналогичным способом можно решить задачу для длинного цилиндра с поперечной поляризацией (без учета неоднородности

Гл.4. Диэлектрики в электростатическом поле	139

поля на торцах). В этом случае коэффициенты деполяризации в его поперечном сечении равны 12 , а продольный равен нулю (это используется далее в задаче 4.4.13).

Задача 4.3.18. В однородное электрическое поле напряженности Е0 поместили однородный диэлектрический шар, проницаемость которого равна ε. Найти напряженность E электрического поля внутри шара и вектор поляризации P диэлектрика.

Решение

Шар представляет собой диэлектрик, для которого выполняются соотношения (4.4) и (4.7): P = ε0(ε – 1)E, где E = E0 + E1, E – полное электрическое поле внутри шара, E1 – поле, созданное поляризационными поверхностными зарядами и найденное в предыдущей

задаче: E = − P . Подставляя выражение для E1 и выполняя ал-
1	3ε0
гебраические преобразования, находим:
Ответ: P = 3ε		ε −1 E		;	E = 3	1	E		.
		0 ε + 2	0			ε + 2		0

Замечание: Обратите внимание, что вектор Р определяется напряженностью полного поля Е внутри тела.

Задача 4.3.19. Пространство между пластинами плоского конденсатора заполнено диэлектриком с проницаемостью ε. Внутри диэлектрика имеется сферическая полость. На пластинах конденсатора равномерно распределены заряды с плотностями σ и –σ. Найти напряженность электрического поля в полости E0.

Решение

Напряженность поля в полости E0 можно представить как разность векторов напряженности однородного поля E в конденсаторе с диэлектриком без полости и поля E1, созданного однородно поляризованным шаром из диэлектрика (рис. 4.18). Поле Е вычислено в

σ

задаче 4.3.2 и равно E = ε0ε .

140	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Поле E1 было вычислено в

P

задаче 4.3.17 и равно E1 = − 3ε0 , где P = ε0(ε –1)E. Отсюда следует:

ε + 2

E0 = E – E1 = σ 3ε0ε .

Ответ: Поле в полости однородно, сонаправлено с внешним полем и равно по величи-

ε + 2 σ не E0 = 3ε ε0 .

PP

	P
	ε
E	E0
	E1

εε

Рис. 4.18. Вычисление напряжённости поля в полости внутри диэлектрика (задача 4.3.19)

§ 4.4. Задачи для самостоятельного решения

4.4.1. Сторонние заряды равномерно распределены с объёмной плотностью ρ > 0 по шару радиуса R из однородного изотропного диэлектрика с проницаемостью ε. Найти:

а) модуль вектора напряженности электрического поля как функцию расстояния r от центра шара; изобразить примерные графики зависимостей E(r) и φ(r);

б) объёмную и поверхностную плотности связанных зарядов.

ρ

Ответ: а) E = 3εε0 r при r < R;

ρR3

E = 3ε0r2 при r > R;

б) ρ′ = − ε −1ρ , σ′ = ε −1ρR . ε 3ε

4.4.2 Бесконечно большая пластина из однородного диэлектрика с диэлектрической проницаемостью ε заряжена равномерно с объёмной плотностью ρ. Толщина пластины 2d. Найти поверхностную и объёмную плотности связанного заряда.

	Ответ: ρ′ = −	ε −1		ρ ;	σ′ =	ε −1		ρd .
		ε				ε