с инета для метод

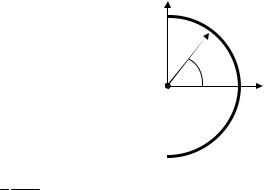
Гл.1. Постоянное электрическое поле

51

1.4.19. В центре полукольца радиуса R находится точечный заряд –q. Полукольцо имеет полный заряд +q, распределенный по закону τ(ϑ) сosϑ, где τ – линейная плотность заряда, ϑ – угол между радиусом-вектором рассматриваемой точки и осью симметрии системы Z (рис. 1.26). В дипольном приближении найти напряженность электрического поля на оси Z на расстоянии z от системы (z >> R).

1 qR

Ответ: E(z) = 8 ε0 z3 .

x

Rq

ϑ

–q z

Рис.1.26. Система из точечного заряда и неравномерно заряженного полукольца (задача

1.4.19)

Литература к главе 1

1.Матвеев А.Н. Электричество и магнетизм. –М.: Оникс 21 век, 2005, §§ 1-3, 5-7, 12,13.

2.Сивухин Д.В. Общий курс физики. Электричество. –М.: Физматлит, 2006, §§ 1 – 9.

3.Калашников С.Г. Электричество. –М.: Физматлит, 2003. §§ 8-15.

4.Тамм И.Е. Основы теории электричества. – М.: Физматлит, 2003, §§ 1- 4, 13.

52	ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Глава 2

РАБОТА СИЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. ПОТЕНЦИАЛ

§2.1 Теоретический материал

Работа сил электростатического поля при перемещении точечного заряда q из точки 1 в точку 2 определяется линейным интегралом

A12 = ∫q(Edl) ,	(2.1)
(L12 )

где L12 – траектория движения заряда, dl – бесконечно малое перемещение вдоль траектории. Если контур замкнутый, то для инте-

грала используется символ ∫; в этом случае предполагается, что выбрано направление обхода контура.

Электростатическое поле потенциально: при перемещении точечного заряда по любому замкнутому контуру работа равна нулю. При произвольном перемещении заряда из точки 1 в точку 2 работа не зависит от траектории, а определяется только положением начальной и конечной точек 1 и 2. Благодаря этому работу поля

можно представить в виде
A12 = q [φ(r1) – φ(r2 )],	(2.2)

где скалярная функция φ(r) называется электростатическим потенциалом. Эта функция непрерывна во всем пространстве и имеет конечные первые производные.

Потенциал является энергетической характеристикой электростатического поля, его можно определить через потенциальную энергию W(r) пробного заряда q в электростатическом поле

φ(r) = W(r) . q

Потенциал в точке r численно равен потенциальной энергии единичного положительного точечного заряда, находящегося в этой точке.

Физический смысл имеет только разность потенциалов двух точек, поэтому потенциал, как и потенциальная энергия, оп-

Гл. 2. Работа сил электростатического поля. Потенциал

53

ределен с точностью до произвольной постоянной, связанной с выбором начала его отсчета.

Нормировка потенциала – придание однозначности потенциалу путем приписывания ему определенного значения в какойлибо точке. Обычно используют один из двух наиболее удобных способов нормировки:

1)если заряды занимают ограниченную область пространства, то принимают равным нулю значение потенциала в бесконечно удаленной точке;

2)если проводящее тело каким-то образом соединено с Землей (заземление), то его потенциал равен потенциалу Земли (потенциал Земли можно положить равным нулю).

В модельных задачах, где заряды занимают бесконечные области (например, бесконечная заряженная плоскость, нить, цилиндр и т.д.), выбор нулевой точки потенциала произволен и определяется соображениями симметрии и удобством записи результата.

Потенциал поля точечного заряда q равен

φ(r) =	1			q	,	(2.3)
	4πε	0		r

где r – расстояние от заряда q до точки наблюдения (потенциал в точке, бесконечно удалённой от заряда принимается равным нулю).

Потенциал поля системы точечных зарядов равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов (принцип суперпозиции для потенциалов).

ϕ = ∑ϕi	=	1		∑	qi	,	(2.4)
i	4πε		0 i		r
					i

где ri – расстояние от точки, в которой вычисляется потенциал, до i- ого заряда.

Потенциал поля точечного диполя равен

φ(r) =	1		pr	(2.5)
	4πε0		r3

(начало координат взято в точке нахождения диполя).

Потенциал поля непрерывного распределения зарядов: если все заряды расположены в конечной области пространства и потенциал нормирован на нуль в бесконечности, то

54 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

φ =	1	∫			dq(r′)			,	(2.6)
	4 πε				r − r′
	0

где r′ – радиус-вектор заряда dq, r – вектор, проведенный из точки, в которой вычисляется потенциал, до заряда dq(r′) в бесконечно малой окрестности точки r′. Интегрирование производится по всем объемам, содержащим распределенные с плотностью ρ заряды (dq(r′) = ρ(r′)dV), по всем поверхностям, несущим поверхностные заряды σ (dq(r′) = σ(r′)dS), и по всем линиям, на которых находятся распределенные с линейной плотностью τ заряды (dq(r′) = τ(r′))dl.

Циркуляцией произвольного вектора A по замкнутому контуру L называется линейный интеграл

∫Adl .	(2.7)
L

Ротором вектора A называется вектор, проекция которого на положительное направление нормали n равна пределу отношения циркуляции вектора А по физически бесконечно малому контуру L к площади S, ограниченной этим контуром

rot		A = lim	1	∫	Adl	(2.8)
	n
		S→0	S
				L

Положительное направление нормали n согласуется с направлением обхода контура L правилом правого винта.

В декартовой системе координат с ортами i, j, k ротор можно представить в виде векторного произведения:

	i		j		k
rot A = [ A ]=	∂		∂		∂		,	(2.9)
	∂x		∂y		∂z
	Ax		Ay		Az

где символический дифференциальный векторный оператор (набла) определен в §1.1. главы 1. В декартовых координатах он имеет вид:

= i	∂	+ j	∂	+ k	∂	.
	∂x		∂y		∂z

Формула Стокса: циркуляция вектора A по произвольному контуру L равна потоку ротора вектора A через любую поверхность, опирающуюся на контур L:

Гл. 2. Работа сил электростатического поля. Потенциал	55
∫Adl =∫rot AdS .	(2.10)

LS

Теорема о циркуляции вектора E (интегральная формулировка потенциальности электростатического поля): в любом электростатическом поле циркуляция вектора E по любому замкнутому контуру L равна нулю

∫Edl =0.	(2.11)
L

Дифференциальная формулировка потенциальности электростатического поля: в любом электростатическом поле в любой точке

rot E = 0.

(2.12)

Градиентом скалярной функции φ назывaeтся вектор

grad φ = ϕ = i	∂ϕ + j	∂ϕ + k	∂ϕ .	(2.13)
	∂x	∂y	∂z

Этот вектор направлен перпендикулярно к поверхности φ = const в сторону возрастания φ, а его модуль равен производной от функции φ по этому направлению.

Два полезных математических тождества:
div rot A ≡ 0 для любой векторной функции A(r);	(2.14)
rot grad φ ≡ 0 для любой скалярной функции φ(r).	(2.15)

Эквипотенциальная поверхность – поверхность, на которой потенциал остается постоянным. Линии напряженности поля перпендикулярны к эквипотенциальным поверхностям и направлены в сторону убывания потенциала.

Связь потенциала с напряженностью поля

E = – grad φ.

(2.16)

Обратная операция – нахождение разности потенциалов Δϕ21 из заданной напряженности поля

(2)
ϕ2 – ϕ1 = − ∫Edl ,	(2.17)
(1)

где интегрирование идет по любой траектории, соединяющей точки 1 и 2.

56 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Дифференциальное уравнение для потенциала (уравнение

Пуассона)
Δφ = –	ρ	,	(2.18)
	ε
0

где – оператор Лапласа. В декартовой системе координат оператор Лапласа является суммой вторых производных по всем координатам:

≡ 2 =	∂2	+	∂2	+	∂2	.	(2.19)
	∂x2		∂y2
					∂z2

В сферической системе координат (r, ϑ, ϕ) оператор Лапласа имеет вид

∂2

2 ∂

1

1 ∂2

∂2

∂

=

+

+

+

+ ctgθ

.

(2.20)

∂r

r

∂r

r

ϑ ∂ϕ

∂ϑ

2

2

sin

2

2

2

∂ϑ

В областях, где заряды отсутствуют, уравнение Пуассона переходит в уравнение Лапласа:

Δφ = 0.

(2.21)

§2.2. Основные типы задач (классификация)

2.1.Определение потенциала или разности потенциалов поля заданного распределения зарядов. Вычисление работы по перемещению заряда в поле заданной системы зарядов.

2.2.Обратная задача: найти распределение зарядов, создающих заданные значения потенциала или разности потенциалов.

2.3.Определение потенциала или разности потенциалов, если задана или легко вычисляется напряженность поля, и обратная задача: найти напряженность поля, если известно распределение потенциала или задана разность потенциалов.

2.4.Построение картины силовых линий и эквипотенциальных поверхностей для заданной системы неподвижных зарядов.

§2.3. Методы решения и примеры решения задач

Так же, как в главе 1, из анализа условий задачи следует определить, к какому типу относится данная задача. Следует уяснить, какими свойствами симметрии обладает изучаемая система зарядов

Гл. 2. Работа сил электростатического поля. Потенциал

57

и полей. В соответствии с этими сведениями надо выбрать наиболее удобную для расчетов систему координат. После того как решение получено, следует обязательно проверить его размерность, соответствие результата различных предельных случаев ожидаемым или ранее полученным результатам, а также рассмотреть физическую картину при различных значениях параметров системы.

Задачи типа 2.1

Определение потенциала или разности потенциалов поля заданного распределения зарядов

Метод решения – прямое суммирование потенциалов в заданной точке от точечных зарядов (2.3), диполей (2.5) и непрерывно распределенных зарядов (2.6). Этот метод универсален, т.е. применим к любому распределению зарядов. Однако, в случае симметричной системы зарядов (как в задачах типа 1.2.3 главы 1), когда с помощью теоремы Гаусса легко выполняется вычисление напряженности поля E, можно свести задачу к типу 2.2.3 и найти потенциал из известной напряженности поля (2.17). Такой подход часто позволяет существенно упростить расчеты.

Если заряды распределены в конечной области пространства, то в дальнейшем (если не оговорено другое условие) будем полагать равным нулю значение потенциала в бесконечно удаленной точке.

Потенциал φ(r) – скалярная функция, поэтому суммирование выполняется алгебраически, что значительно упрощает расчет по сравнению с вычислением напряженности поля E(r), когда вклады от разных зарядов складываются векторно.

Наиболее общий подход состоит в использовании уравнения Пуассона (или уравнения Лапласа). При этом учитываются условия непрерывности потенциала, граничные условия и условия нормировки. Однако решение дифференциального уравнения второго порядка в частных производных является достаточно сложной задачей и в курсе общей физики практически не используется. Отдельные примеры применения этого метода можно найти в некоторых учебниках (см., например, [1], § 15). Другое дело – использование уравнения Пуассона для решения обратной задачи. Если задано распределение потенциала, то, вычисляя его вторые производные по координатам, можно с помощью уравнения Пуассона найти распределение заряда во всем пространстве.

58

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Задача 2.3.1 (базовая задача). Найти потенциал поля, созда-

ваемого равномерно заряженной с линейной плотностью τ нитью

длины 2L.

z

Решение

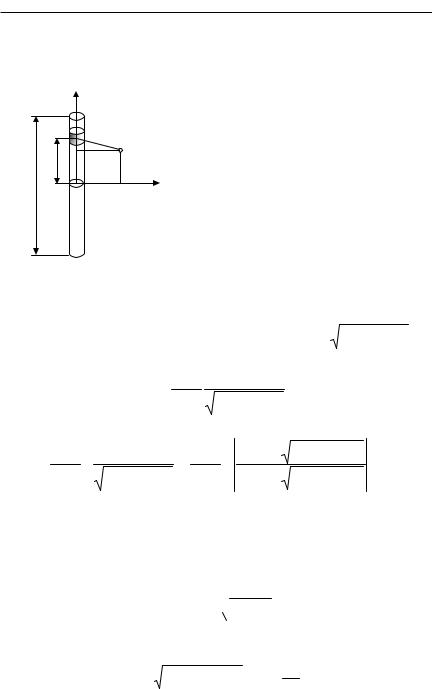
Поместим начало координат в цен-

dl M(r,z)

тре нити и направим ось Z вдоль ни-

ти. Система зарядов аксиально сим-

l

z

метрична, поэтому для расчетов вы-

2L

r

r

берем цилиндрическую систему ко-

0

ординат r, φ, z, в которой потенциал

в произвольной точке М зависит

только от переменных r и z (рис.2.1,

для наглядности нить показана в ви-

Рис. 2.1. К нахождению потенциа-

де тонкого цилиндра). Выделяем на

ла поля, создаваемого заряженной

нити на расстоянии l от центра бес-

нитью (задача 2.3.1)

конечно малую область с зарядом

dq = τ dl,

который

можно

считать

точечным. Его расстояние до точки М(r, z) равно

r2 + (l − z)2 , а

создаваемый им потенциал определяется формулой (2.3):

dφ =

1

τdl

.

4πε0

r2 + (l − z)2

Потенциал, создаваемый всей нитью, равен

τ L

dl

τ

z + L + r2 + (z + L)2

ϕ =

4πε0 −∫L

r2 + (l − z)2

=

4πε0

ln z − L +

r2 + (z − L)2 .

(2.22)

Анализ результата и дополнительные выводы.

1.

При удалении на очень большое расстояние (z→ ∞ или

r → ∞) система выглядит как точечный заряд. Если в полученном

результате сделать предельный переход z→ ∞ или r → ∞, то дол-

жен получиться потенциал точечного заряда. Выполним такой пре-

дельный переход.

Если ввести переменную R = 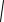z2 + r2 , то любой из упомяну-

тых двух предельных переходов выполняется, если R → ∞. Тогда при очень больших значениях R (R >> L) имеем:

r2 + (z ± L)2 ≈ R ± zL ,

R

Гл. 2. Работа сил электростатического поля. Потенциал

59

L +

zL

zL

zL

zL

R

z + L + R +

1+

L +

L −

R + z

R

R

R

ln

z − L + R −

zL

= ln

L −

zL

= ln 1

+

R + z

− ln 1

−

R + z

≈

R

R

1−

R + z

L +

zL

− L −

zL

2L + 2

zL

R

R

2L

≈

−

=

R

=

.

R + z

R + z

R + z

R

Отсюда получаем, что на больших расстояниях от нити потенциал приближенно равен потенциалу поля точечного заряда

φ ≈	2Lτ		=	q			,
				4πε
4πε		R			0	R
	0

где q = 2Lτ – полный заряд нити.

2. Если L → ∞, то потенциал стремится к бесконечности. Потенциал остается ограниченной функцией, если только все заряды сосредоточены в области конечных размеров, а здесь заряды имеются в бесконечно удаленной области. В этом случае непосредственный физический смысл имеет только разность потенциалов в любых двух точках. В случае бесконечной нити разность потенциалов находим из (2.22) для точек 1 и 2, удаленных от оси нити на расстояния r и R (r < R)

Δφ12	= φ(r) – φ(R) = −	τ		ln	r	.	(2.23)
	2πε		0		R

Поясним сказанное расчетом. При L → ∞ потенциал не зависит от z и в (2.22) можно положить z = 0. Кроме того, r << L и

r2

L + L2 + r2

4L

2

2

L + r

≈ L 1+

,

≈1+

.

2

− L +

2

+ r

2

r

2

2L

L

Из (2.22) находим:

τ

4L

4L

φ(r) – φ(R) ≈

ln 1

+

− ln 1+

≈

r

2

R

2

4πε0

≈

τ

ln

R2

= −

τ

ln

r

.

4πε

r2

2πε

0

0

R

60ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Вслучае бесконечной нити задачу можно отнести к типу 2.2.3. В главе 1 получено выражение для напряженности поля бесконеч-

τ

ной равномерно заряженной нити: E = Er = 2πε0r . Согласно (2.17)

	r	τ		r
	φ(r) – φ(R) = − ∫Edr = −		ln		,
		2πε0
	R			R

что совпадает с (2.23).

3. Компоненты напряженности поля можно найти из (2.22), вычисляя градиент потенциала, т.е. используя (2.16). Ввиду аксиальной симметрии системы, целесообразно расчет выполнить в ци-

∂ϕ ∂ϕ

линдрических координатах, где Ez = − ∂z , Er = − ∂r . Проекция Еφ

в нашем случае равна нулю. Этот расчет мы предоставляем сделать читателю. Результат будет полезно сравнить с полученным выше в задаче 1.3.3.

Ответ: ϕ(r z) =	τ	ln	z + L +	r2 + (z + L)2				.
4πε0			z − L +	r2 + (z − L)2

Задача 2.3.2 (базовая задача). На тонком кольце радиуса R

распределен по произвольному закону заряд q. Определить потенциал поля в точке А, расположенной на оси кольца на расстоянии h от его плоскости.

Решение

Потенциал бесконечно удаленной точки будем считать равным нулю. На кольце выделим дугу бесконечно малой длины dl. Заряд dq этого участка рассматриваем как точечный. В точке наблюдения

1dq

Аон создает потенциал dϕ = πε0 r , где r = R2 + h2 . Суммиро-

вание всех таких вкладов при любом распределении заряда на

кольце дает ответ: ϕ =	1			q		. В частности, в центре кольца
4πε0				R2 + h2

1q

ϕ= πε0 R . Эти результаты можно было сразу записать без всяких

вычислений, так как все части распределенного заряда находятся на одном и том же расстоянии от центра кольца.