Решение систем линейных уравнений

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

1.ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Кзадаче решения системы линейных алгебраических уравнений (СЛАУ) сводится большое число физических и технических проблем, возникающих, например:

-при решении задач статической и динамической теории упругости, упругопластичности, акустики и др.;

-при анализе работы электрических цепей;

-при анализе процесса распространения тепла в сплошной среде (газе, жидкости или твёрдом теле) от более нагретых частей к менее нагретым;

-и т.д.

1.1.ЗАДАЧИ, СВЯЗАННЫЕ С АНАЛИЗОМ РАБОТЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Задачи, связанные с анализом работы электрических цепей, могут формулироваться разными способами, например:

-расчет токов в системе;

-нахождение электродвижущей силы (ЭДС);

-вычисление внутренних сопротивлений источников ЭДС;

-расчет значений сопротивления каждой ветки электрической цепи.

Математическая модель для такого рода задач создается на ос-

нове законов Кирхгофа.

В изолированной замкнутой электрической цепи выполняются следующие законы Кирхгофа:

1.Алгебраическая (с учетом знаков) сумма входящих и выходящих токов для любого узла контура равна нулю, т.е. сколько тока

«втекает» в узел по одним ветвям (эти токи берутся со знаком «+»), столько из него «вытекает» по другим (эти токи берутся со знаком «–»). Математически это можно выразить следующим образом:

N
∑I k = 0 ,	(1.1)

k =1

1

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

где N – общее количество узлов цепи, k – номер узла.

Узлом называется такая точка электрической схемы, в которой сходятся как минимум три тока. Все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия.

2.Алгебраическая сумма падений напряжения на элементах в лю-

бом контуре равна нулю, то есть алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений на пассивных элементах этого контура.

При суммировании ЭДС падения напряжений берутся со знаком «+», если их направления совпадают с произвольно выбранным направлением обхода контура и со знаком «–» в противном случае.

Считается, что если при выбранном положительном направлении обхода контура первым встречается положительный полюс источника, то ЭДС будет отрицательной, если первым встречается отрицательный, то ЭДС будет положительной. Математически это можно записать следующим образом:

NR	N E
∑I k Rk = ∑Ei ,		(1.2)
k =1	i=1

где N R и N E – число пассивных элементов и ЭДС в контуре соответственно.

Замечание. Если в схеме присутствуют реальные источники тока, то их, при помощи эквивалентных преобразований, следует заменить на идеальные. В случае с источниками постоянного тока, отличие реальных от идеальных заключается в том, что реальные источники тока обладают внутренним сопротивлением, которое обозначается как ri . Следовательно, математическое представление второго закона Кирхгофа можно заменить на следующее:

2

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..
NR	NR	N E
∑I k Rk + ∑I k rk = ∑Ek .			(1.3)
k =1	k =1	k =1

Эти уравнения применяются только к одному контуру. Между тем, вся электрическая схема может быть разбита на несколько контуров. Для каждого из замкнутых контуров, которые можно мысленно выделить в разветвленной цепи, можно составить приведенные выше уравнения, однако, независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга.

Задача 1. Проанализировать работу электрической цепи из линейных элементов по приведенной многоконтурной схеме (рис. 1.1): найти неизвестные токи i1, i2, i3 по заданным значениям сопротивлений R1, R2, R3 и электродвижущей силе источника тока E.

Исходными данными для решения этой задачи являются: значения сопротивлений и электродвижущая сила источника тока. Резуль- татом являются значения токов.

Все величины представлены в системе измерения СИ. Все величины – вещественного типа.

Рис. 1.1. Многоконтурная схема электрической цепи к задаче 1

3

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Для электрической цепи, изображенной на рис. 1.2, закон Кирхгофа для токов в узле b:

i1 = i2 + i3.

Закон Кирхгофа применительно к левому и внешнему контурам цепи:

E− U 2 − U1 = 0,

E− U 3 − U1 = 0.

Выразив напряжения через токи и сопротивления, получим:

E − i2 R2 − i1 R1 = 0,

E − i3 R3 − i1 R1 = 0.

Таким образом, получается система трех уравнений с тремя неизвестными i1, i2 и i3. Ее можно записать так, чтобы в правых частях уравнений находились неизвестные, умноженные на соответствующие коэффициенты, а в левых – свободные члены:

1 i		− 1 i			−	1 i = 0
	1			2		3
R1		i1	+ R2 i2 + 0 i3 = E				(1.4)
		i1	+ 0 i2			+ R3 i3 = E
R1

Матрица коэффициентов и вектор правых частей системы запишутся так:

	1		− 1		− 1						0
A =	R										E	.
			R		0			, b =
		1		2
	R		0		R	3					E
		1

Это и есть математическая модель этой задачи. Таким образом, ее решение сводится к решению системы линейных уравнений (1.4) относительно i1, i2, i3.

Задача 2. Проанализировать работу электрической цепи по многоконтурной схеме, приведенной на рис. 1.2. Найти неизвестные токи ik, (k = 1, …, 6) по заданным значениям сопротивлений и электродвижущей силе источника тока.

4

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Рис. 1.2. Многоконтурная схема электрической цепи к задаче 2

Исходными данными для решения этой задачи являются: значения сопротивлений и электродвижущая сила источника тока.

Результатом являются значения токов.

Все величины представлены в системе измерения СИ. Все величины – вещественного типа.

Составим математическую модель. Данную схему можно разбить на несколько контуров:

1)1-2-5-4-1;

2)4-5-7-6-4;

3)2-3-8-7-5-2;

4)1-2-3-8-7-6-4-1;

5)1-2-5-7-6-4-1;

6)2-3-8-7-6-4-5-2; и так далее.

Однако можно заметить, что контуры, начиная с четвертого и далее можно получить наложением первых трех. Поэтому будем рассматривать только три контура:

1)1-2-5-4-1;

2)4-5-7-6-4;

3)2-3-8-7-5-2.

5

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Зададим направление обхода в каждом из контуров по часовой стрелке, и запишем уравнения согласно второму правилу Кирхгофа:

Контур	Уравнение
1-2-5-4-1	I1R1 + I3 R3 + I5 R5 = −E1
4-5-7-6-4	− I5 R5 + I 4 R7 + I 6 R9 + I 6 R6 = −E2 + E1
2-3-8-7-5-2	I 2 R2 + I 2 R4 + I 2 R8 − I 4 R7 − I3 R3 = −E4 + E3

Теперь запишем уравнения для каждого из узлов (первый закон Кирхгофа):

Узел	Уравнение
2	I1 − I 2 − I 3 = 0
4	I5 + I6 − I1 = 0
5	I3 − I 4 − I5 = 0

7I 4 + I 2 − I 6 = 0

Таким образом, мы получили 7 уравнений – 3 для контуров и 4 для узлов.

Однако, если посмотреть на уравнения для узлов, то видно, что сумма первых трех уравнений дает четвертое уравнение (для узла 7):

I1 − I 2 − I 3 + I 5 + I 6 − I1 + I 3 − I 4 − I 5 = −I 2 − I 4 + I 6 .

Следовательно, можно выбрать лишь три из них. Выбираем первые три. Получим систему из шести уравнений и шести неизвестных:

6

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

I1R1 + I3 R3 + I5 R5 = −E1

− I5 R5 + I 4 R7 + I6 R9 + I6 R6 = −E2 + E1

I

R

+ I

R

+ I

R

− I

R

− I

R

= −E

+ E

2

2

2

4

2

8

4

7

3

3

4

3

(1.5)

I1 − I2 − I3 = 0

I

+ I

− I

= 0

5

6

1

I3 − I4 − I5 = 0

или

R1 I1 + 0 I

2 + R3 I3 + 0 I 4 + R5 I5 + 0 I6 = −E1

I1

+ 0 I 2

+ 0 I3 + R7 I4 − R5 I5 + (R6 + R9 ) I6 = −E2 + E1

0

0 I1 + (R2 + R4 + R8 ) I 2 − R3

I3 − R7

I4 + 0 I5

+ 0 I6 = E3 − E4

(1.6)

I1 − I2 − I3 + 0 I 4 + 0 I5 + 0 I6 = 0

− I + 0 I

+ 0

I

+ 0

I

+ I

+ I

= 0

1

2

3

4

5

6

I1

+ 0

I 2

+ I3 − I4 − I5 + 0

I6 = 0

0

Замечание. Следует отметить, что обычно, при записи всех уравнений, вытекающих из правил Кирхгофа мы получаем «лишние» уравнения, то есть такие уравнения, которые можно получить алгебраической суммой или разностью других. Чтобы не выписывать «лишние» уравнения следует руководствоваться следующим принципом: не нужно выписывать уравнения, все члены которого уже были в предыдущих. Таким образом, если бы мы применили данный принцип в рассматриваемой задаче, то стало бы ясно, что четвертое уравнение для узлов можно было вообще не выписывать, поскольку все токи, входящие в него, уже встречались в предыдущих уравнениях.

Таким образом, в матричном виде система линейных уравнений (1.5) запишется так:

AI = b ,

где

7

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

R		0	R		0	R		0
	1			3			5
	0	0	0		R7	− R5		R6 + R9
0 R2 + R4 + R8			− R3		− R7	0		0
A =	1	− 1	− 1		0	0		0	,
− 1		0	0		0	1		1
					− 1	− 1
0		0	1					0

								I1									− E1
								I							E			− E
										2					1					2
								I		3					E3 − E4
						I =					,		b =							.
								I 4										0
								I		5								0
								I 6										0
	Это и есть математическая модель задачи, ее решение сводится
к решению системы линейных уравнений (1.5).
Пример к задаче 2. Пусть сопротивления приборов																							и ЭДС имеют
следующие значения:
	R1	R2	R3					R4						R5				R6			R7		R8	R9
	20	40	10				32						12					18			50		5	11
					E1						E2				E3					E4
					12						6				15					36

Тогда в матричном виде система (1.7) будет иметь вид:

8

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

20 0 10						0	12		0			I1				− 12
		0	0		0	50	− 12 29
												I 2			6
												I				− 21
0 77 − 10 − 50							0		0
			− 1		− 1								3		=
		1				0	0		0			I 4			0
− 1 0					0	0	1		1			I				0
													5
			0		1	− 1
0							− 1 0					I6				0
Если решить данную систему, то получим следующие значения
токов:
			I1		I 2	I 3			I 4			I 5				I 6
		-0,37			-0,22	-0,15		0,12			-0,26				-0,1

Отрицательные значения токов говорят о том, что их направление выбрано не верно, то есть на самом деле при указанных значениях сопротивлений и ЭДС все токи кроме тока номер 4 направлены в сторону, обратную указанной на схеме. Таким образом, не стоит ломать голову над тем, в какую сторону направить токи – направляйте как угодно, решение само подскажет верное направление.

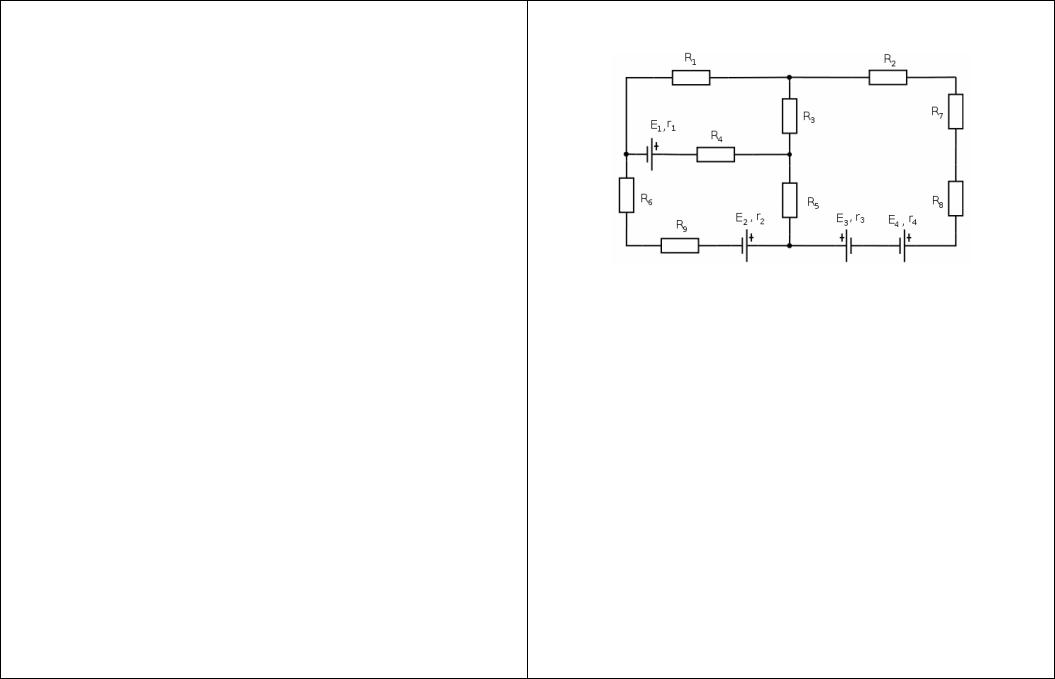
Задача 3. Пусть дана электрическая схема, представленная на рис. 1.3. В этой схеме присутствуют реальные источники тока. Известны сопротивления пассивных элементов Ri (i = 1,K9) , напряже-

ния на контактах Ei (i = 1,K4) и внутреннее сопротивление источни-

ков токов ri (i = 1,K4) . Необходимо при помощи законов Кирхгофа и метода контурных токов определить токи в ветвях этой цепи.

9

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Рис. 1.3. Исходная схема задачи 3

Исходными данными для решения этой задачи являются: сопротивления пассивных элементов, напряжения на контактах и внутренние сопротивления источников токов.

Результатом являются значения токов.

Все величины представлены в системе измерения СИ.

Все величины – вещественного типа.

Составим математическую модель. Преобразуем схему так, чтобы в каждой ветви осталось только по одному активному и/или пассивному элементу. Для этого заменим несколько последовательно соединенных пассивных элементов, суммой их сопротивлений. Сделаем то же самое с источниками ЭДС. В результате получим схему, представленную на рис. 1.4.

10

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

.

Рис. 1.4. Преобразованная схема задачи 3

При этом получаем следующие величины:

R* = R + R ,			R* = R + R + R ,				E* = E − E		4	.
6	6	9	2	2	7	8	3	3

Схему (1.4) можно разбить на несколько контуров:

1)1-2-4-1;

2)3-4-2-3;

3)1-4-3-1;

4)1-2-3-4-1;

5)и так далее.

Заметим, что контуры, начиная с четвертого и далее можно получить наложением первых трех. Поэтому будем рассматривать только три контура:

1)1-2-4-1;

2)3-4-2-3;

3)1-4-3-1.

Зададим направление обхода в каждом из контуров по часовой стрелке (рис.1.5) и запишем уравнения согласно второму правилу Кирхгофа:

11

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Контур			Уравнение
1-4-2-1	I1R1 + I 3 R3 + I 4 R4 + I 4 r1 = −E1
3-2-4-3	− I 4 R4 − I 4 r1 + I 5 R5 + I 6 r2 + I 6 R6 = −E2 + E1
1-3-4-1	*	*	*
	I 2 R2	+ I 2 r3	− I5 R5 − I3 R3 = E3

Рис. 1.5. Электрическая схема задачи 3 с направленными токами и выбранными направлениями обхода

Теперь запишем уравнения для каждого из узлов согласно математическому выражению для первого закона Кирхгофа:

Узел	Уравнение
1	I1 − I 2 − I3 = 0
2	I 4 + I 6 − I1 = 0
3	I5 + I 2 − I 6 = 0
4	I3 − I 4 − I5 = 0
	12

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Таким образом, мы получили 7 уравнений: 3 для контуров и 4 для узлов. Однако согласно замечания, приведенного в задаче 2, ясно, что четвертое уравнение для узлов можно было вообще не учитывать, поскольку все токи, входящие в него, уже встречались в предыдущих уравнениях.

Таким образом, получим систему уравнений из шести уравне-

ний.

I R

+ I

3

R

+ I

4

R

+ I

4

r

= −E

1

1

3

4

1

1

− I

4

R

− I

4

r

+ I

5

R

+ I

6

r

+ I

6

R

= −E

2

+ E

4

1

5

2

6

1

R

*

+ I

r

*

− I

R − I

R

= −E

*

I

2

2

2

3

5

5

3

3

3

(1.7)

I1 − I2 − I3 = 0

I

+ I

− I

= 0

5

2

6

− I4

− I5 = 0

I3

или

R1 I1 + 0 I 2 + R3 I3 + (R4 + r 1) I 4 + 0 I5 + 0 I 6 = −E1

I1

+ 0 I 2 + 0 I3

− (R4 + r 1) I 4 + R5 I 5 + (R6 + r2 ) I 6 = −E2 + E1

0

I1

+

*

*

+ 0 I 6

*

0

(R2 + r3 ) I 2 − R3 I 3 + 0 I 4 − R5 I5

= −E3

I1 − I 2 − I3 + 0 I 4 + 0 I 5 + 0 I 6 = 0

(1.8)

0 I1 + I 2 + 0 I3 + 0 I 4 + I5 − I 6 = 0

I1

+

0

I 2 + I3 − I 4 − I 5 + 0

I 6

= 0

0

Таким образом, в матричном виде система линейных уравнений (1.7) запишется так:

AI = b ,

где

13

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

R1		0		R3	R4 + r 1				0		0
	0	0		0	− R		− r		R	R	+ r
		R* + r *				4		1	5	6	2
0				− R		0			− R		0
A =		2	3	3					5			,
	1	− 1		−1		0			0		0
	0	1		0		0			1	−1
					− 1				−1
0		0		1							0

I1

− E1

I

E

− E

2

1

2

I

3

− E3*

I =

,

b =

.

I 4

0

I

5

0

I 6

0

Это и есть математическая модель задачи, ее решение сводится

к решению системы линейных уравнений (1.7).

Найдем значения токов на каждом из приборов при известных

значениях

сопротивлений

приборов

( R = 20 ,

R*

= 77 ,

R

3

= 10 ,

1

2

R

4

= 12 , R

5

= 50 ,

R* = 29 ) в цепи, ЭДС ( E = 12 ,

E

2

= 6 ,

E *

= −21)

6

1

3

и внутреннее сопротивление ( r

1

= 0,1; r

= 0,4; r*

= 0,45) источников

2

3

тока,

Решение: Итак у нас 6 уравнений и 6 неизвестных. Запишем уравнения, подставив известные значения в (1.8):

20 I1 + 0 I 2 + 10 I 3 + (12 + 0,1) I 4 + 0 I 5 + 0 I 6 = −12
0	I1		+ 0	I 2 + 0 I3 − (12		+ 0,1) I 4 + 50 I 5 + (29 + 0,4) I 6 = −6 + 12
0	I1		+ (77 + 0,45) I 2 −10 I 3 + 0 I 4 − 50 I 5 + 0 I 6 = 21
I1 − I 2 − I3 + 0 I 4 + 0 I 5 + 0 I 6 = 0
0 I1 + I 2 + 0 I3 + 0 I 4 + I5 − I 6 = 0
		I1	+ 0		I 2 + I3 − I 4 − I	5 + 0		I 6 = 0
0
								14

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

В более привычном виде эту систему можно записать так:

20		0	10	12.1	0	0		I1			−12
0		0	0	− 12.1	50	29.4		I 2			6
			− 10		− 50
	0	77.45		0		0		I3		=	21
1		−1	−1	0	0	0		I 4		0
	0	1	0	0	1	−1					0
								I5
		0	1	−1	−1	0					0
0								I 6
Решая данную систему, находим неизвестные токи на схеме:
I1 = −0,365А,		I 2 = −0,216A,			I 3 = −0,149 A,						I 4 = −0,265A,

I 5 = 0,115 A, I 6 = −0,101A.

Отрицательные значения токов говорят о том, что их направление выбрано не верно, то есть на самом деле, при указанных значениях параметров системы, все токи, кроме тока номер 4, направлены в сторону, обратную указанной на схеме. Таким образом, токи при решении задачи токи можно направлять в любую сторону – решение само подскажет верное направление.

Алгоритм решения задач 1, 2, 3 можно применить и к таким задачам как: нахождение токов в системе, нахождение ЭДС, внутренних сопротивлений источников ЭДС, нахождение значений сопротивления каждой ветки, чтобы в системы были указанные значения токов и так далее.

Для этого:

1.Определяем независимые контуры, задаем направления обхода в контурах.

2.Определяем узлы. Направляем в узлах токи.

3.Выписываем уравнения для контуров и узлов.

4.Проверяем полноту системы, чтобы число независимых уравнений совпадало с числом неизвестных.

5.Составляем систему уравнений и решаем ее любым известным методом.

15

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

1.2.ЗАДАЧИ, СВЯЗАННЫЕ С АНАЛИЗОМ ПРОЦЕССА РАСПРОСТРАНЕНИЯ ТЕПЛА В СПЛОШНОЙ СРЕДЕ

Рассмотрим построение математической модели задачи о распространении тепла в некоторой среде (газе, жидкости или твёрдом теле) от более нагретых частей к менее нагретым. Среда (область) распространения тепла часто имеет очень сложную форму, может состоять из различных сред, имеющих сложные свойства.

Математическая модель для такого рода задач создается на основе законов из области математической физики.

Пусть в некоторой среде распространяется тепловой поток U, меняющийся со временем t, т.е. U (x, y, z, t) , где x, y, z – декартовы координаты. Распределение тепла в этой среде удовлетворяет дифференциальному уравнению в частных производных

∂ 2U	+	∂ 2U	+	∂ 2U	+ F (x, y, z, t ) = a	∂U	,	(1.9)
∂x 2		∂y 2		∂z 2
						∂t

где F (x, y, z, t ) определяет выделение (поглощение) тепла в единицу времени в единице массы тела, например, в результате каких-либо химических реакций;

a – постоянная, зависящая от физических свойств среды распространения тепла.

Постоянная a , вычисляется по формуле a = λ / cρ ,

где λ – коэффициент теплопроводности; c – теплоемкость вещества;

ρ – плотность вещества.

Если в рассматриваемом теле отсутствует выделение или поглощение тепла, то F (x, y, z, t ) ≡ 0 и уравнение (1.9) принимает вид

∂ 2U	+	∂ 2U	+	∂ 2U	= a	∂U	.	(1.10)
∂x 2		∂y 2		∂z 2
						∂t

16

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

При стационарном процессе распространения тепла, т.е. если

							∂U
температурный режим не зависит от времени									= 0 , правая часть
							∂t
уравнения (1.10) будет равна нулю
	∂ 2U	+	∂ 2U		+	∂ 2U	= 0 .		(1.11)
	∂x 2		∂y 2			∂z 2

Это уравнение в математической физике называют уравнением Лапласа.

Если вычислять распределение температуры в плоском теле, на-

	пример, в пластине, то задача становится двумерной, т.е.					∂ 2U	= 0 . В
						∂z 2
	этом случае получим уравнение
		∂ 2U	+	∂ 2U	= 0 .		(1.12)
		∂x 2		∂y 2

Уравнение в частных производных имеет бесконечное множество решений. Для выделения единственного решения необходимо на решение рассматриваемого уравнения наложить дополнительные условия. Дополнительные условия в зависимости от их физического смысла разделяются на начальные и граничные (краевые). При этом, условия, относящиеся к начальному моменту времени, называют на- чальными, а условия, относящиеся к фиксированным значениям координат (обычно это координаты граничных точек рассматриваемой области), – краевыми или граничными.

Применительно к уравнению (1.10) начальные условия – это значения искомой температуры тела в начальный момент времени, а граничные условия – это значение температуры на границе рассматриваемой области в любые моменты времени.

Пример задания граничных и начальных условий. Пусть имеется теплоизолированный (кроме концов) однородный нагретый стержень 0 ≤ x ≤ l, где l – длина стержня (рис. 1.6).

17

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

x

0

l

Рис. 1.6. Теплоизолированный однородный нагретый стержень

Температура стержня U = U ( x, t) в точке x для любого момента времени удовлетворяет уравнению теплопроводности

	∂ 2U	= a	∂U	,	(1.13)
	∂x2
			∂t
где a – постоянная, зависящая от физических свойств стержня.
В начальный момент времени t = t0					для внутренних точек
стержня задано начальное распределение температуры
U ( x, t 0) = f ( x) ,
где f ( x) – известная функция.
На концах стержня заданы условия:
U (0, t) = ϕ ( x) ,
где ϕ ( x) – известная функция.		Например,			если на конце стержня

поддерживается температура 100ºC, то U (0, t) = 100 . Аналогично, для второго конца: если на конце стержня поддерживается темпера-

тура 0ºС, то U (l, t ) = 0 .

При стационарном процессе (1.12) для получения единственного решения достаточно задать только граничные условия.

Уравнение Лапласа в конечных разностях. Общий подход к решению уравнений в частных производных заключается в замене этого уравнения конечно-разностным уравнением.

Классическое определение производной функции одной переменной записывается в виде

dy	= lim	y( x +	x) − y( x)	.
dx x →0			x

Таким образом, при достаточно малом шаге x , производную можно заменить разностью

18

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

dy	≈	y( x +	x) − y( x)	.	(1.14)
dx			x

Такая подстановка называется правой разностью. Аналогично можно получить и другое равенство, называемое левой разностью

	dy	≈	y( x) − y( x − x)		.	(1.15)
	dx			x
В случае стационарного процесса распространения тепла в плос-
ком теле (1.12) имеются две				независимые		переменные

x и y. Применим формулы (1.14) и (1.15) к вычислению частных производных по x и y .

Вначале рассмотрим разности только в направлении x. Заменим

вначале первую производную по x правой разностью
	∂U	=	U ( x +	x, y) − U ( x, y)	.	(1.16)
	∂x			x

Для простоты обозначим				∂U			= U x .
				∂x
Используя (1.15), выведем соотношение для второй производной
	∂ 2U	=	∂U x			U x ( x + x, y) − U x ( x, y)
					=				.
	∂x 2		∂x
								x
Заменим первую производную U x								левой разностью (1.15), чтобы

скомпенсировать эффект «сдвинутости» вправо (1.16) при замене первой производной

	∂ 2U		=	U ( x + x, y) − U ( x, y) − U ( x, y) + U ( x − x, y)					.
	∂x 2						x 2
Таким образом, соотношение для							вычисления второй производной
в направлении x будет иметь вид
		∂ 2U			=	U ( x + x, y) − 2U ( x, y) + U ( x − x, y)		.		(1.17)
		∂x 2					x 2
19

Составители: БикмеевА.Т., КарчевскаяМ.П., КузьминаЕ.А., РамбургерО.Л..

Аналогично, найдем разности для замены второй производной в направлении y:

	∂ 2U			=	U ( x, y +	y) − 2U ( x, y) + U ( x, y −			y)	.	(1.18)
	∂y 2					y 2
Перепишем уравнение Лапласа с учетом соотношений (1.17)
и (1.18)
		U ( x + x, y) − 2U ( x, y) + U ( x − x, y)					+
						x 2					(1.19)
			U ( x, y + y) − 2U ( x, y) + U ( x, y − y)
	+								= 0.
						y 2

Таким образом, значение температуры U в точке ( x, y) можно вычислять как среднее арифметическое значений U в соседних точках по горизонтали и вертикали (рис. 1.7).

Рис. 1.7. Соседние точки по горизонтали и вертикали для ( x, y)

Если принять, что x = y = h , то получим

U ( x + h, y) + U ( x − h, y) − 4U ( x, y ) + U ( x, y + h) + U (x, y − h) = 0

или

U ( x, y) = U ( x + h, y) + U (x − h, y) + U ( x, y + h) + U ( x, y − h) . (1.20) 4

20