Эллипсоид

Эллипсоид (рис.7) (от «эллипс» и греч. «eidos» — вид) - замкнутая центральная поверхность второго порядка. Эллипсоид имеет центр симметрии – и три оси симметрии, которые называются осями. Точки пересечения координатных осей с эллипсоидом называются его вершинами. Сечения эллипсоида плоскостями являются эллипсами (в частности, всегда можно указать круговые сечения эллипсоида). Каноническое уравнение эллипсоида имеет вид:

     - трехосный эллипсоид;

      - эллипсоид вращения вокруг оси ;

      - эллипсоид вращения вокруг оси ;

      - эллипсоид вращения вокруг оси ;

      - сфера.

Рис. 7

Свойства эллипсоида.

1. Эллипсоид – ограниченная поверхность.

2. Эллипсоид обладает:

• центральной симметрией относительно начала координат,

• осевой симметрией относительно координатных осей,

• плоскостной симметрией относительно начала координат.

В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

Форма эллипсоида.

Исследуем форму эллипсоида. Из уравнения видно, что координаты точек поверхности ограничены:

Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат.

Для выяснения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью . Так как любая точка плоскостиимеет нулевую третью координату,, то координаты точек эллипсоида на плоскостиудовлетворяют уравнению:

Получаем, что линия пересечения является эллипсом с полуосями и

Рис. 8. Сечение плоскостью

Аналогично, сечение в плоскости ,  дает эллипс:

с полуосями и, а сечение плоскостью– эллипс:

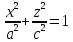
с полуосями и

Рис.9. Сечения эллипсоида координатными плоскостями

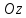Нарисованный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью . Эта плоскость параллельна плоскостии пересекает осьв точке. Уравнения этой линии:

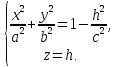
Очевидно, что если , то ни одна точка пространства не может удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой - отрицательное.

Если 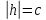, то в сечении получим лишь одну точкуилив зависимости от знака.

Пусть . Тогда первое уравнение преобразуем к виду:

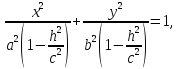
то есть к виду:

где 

Уравнение является уравнением эллипса, подобного эллипсу, задаваемому уравнением, с коэффициентом подобияи полуосямии. Ясно, что сечение плоскостьюявляется таким же эллипсом, расположенным симметрично первому относительно плоскости. Нарисуем эти сечения.

Рис.10. Дополнительные сечения эллипсоида

Таким образом, весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости и подобных эллипсу в плоскости.дает более привычное глазу изображение эллипсоида:

Рис.11. Эллипсоид

Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии - центром эллипсоида. Числа   называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей. Например, если , то все сечения эллипсоида плоскостями, будут окружностями. Сам эллипсоид может быть получен из эллипса:

лежащего в плоскости , при вращении его вокруг оси.

Рис.12. Эллипсоид вращения