Algebra_10kl_RU

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
				П р о д о л ж. т а б л. 28
3. Нечетность функции y = arctg x
		arctg (–a) = –arctg a
Объяснение и обоснование
1. График функции y = arctg x. Функция y = tg x возрастает на промежутке
(− 2π ; 2π ) и принимает все значения от –× до +×. Таким образом, на этом про
межутке функция y = tg x имеет обратную функцию, которая обозначается
y = arctg x, с областью определения (–×; +×) и множеством значений (− π ; π ).
							2	2
Функция y = arctg x также возрастает, и ее график можно получить из графи
ка функции y = tg x (на заданном промежутке) с помощью симметричного
отображения относительно прямой y = x (рис. 90).
2. Значение arctg a. По определению обратной функции (на выбранном про
межутке), если tg ϕ = a, то arctg a = ϕ, причем ϕ (− π ; π ).						Таким образом,
			2	2
запись arctg a = ϕ означает, что ϕ (− π ; π ) и tg ϕ = a. То есть
2	2
	arctg a — это такое число из про
	межутка (− π ;				π ),		тангенс кото
				2	2
	рого равен a.
	Например, arctg					3 = π , посколь
						3	6
	ку π (− π ; π ) и tg π =						3 .
	6	2	2		6		3
	Аналогично arctg (−1) = − π ,
							4
	поскольку − π			(− π ; π ) и tg (− π )= −1.
Рис. 90			4	2		2	4

152

		§ 13. Обратные тригонометрические функции
	3. Нечетность функции y = arctg x. Для
	нахождения арктангенсов отрицатель
	ных чисел можно также пользоваться
	нечетностью функции arctg x, то есть
	формулой arctg (–a) = –arctg a.
	( Это следует из того, что график функ
	ции y = arctg x (рис. 90) симметричен
	относительно начала координат, а
	также из того, что точки a и (–a) на ли					Рис. 91
	нии тангенсов являются симметрич
	ными относительно оси Ox (рис. 91).
	Тогда и соответствующие точки A и B на единичной окружности (на про
	межутке (− π ;	π )) также будут симметричными относительно оси Ox. Та
	2	2
	ким образом, COA = COB. Но arctg a = COA, а arctg (–a) = – COB.
	Получаем
				arctg (–a) = –arctg a . )
			3		3 = − π .
	Например, arctg −			= −arctg
			3		3	6
	Пример Найдите tg (arctg 4).

Р е ш е н и е

X Пусть arctg 4 = ϕ, тогда по опре делению арктангенса получаем, что

tg ϕ = 4.

Таким образом,

tg (arctg 4) = tg ϕ = 4. Y

К о м м е н т а р и й

Поскольку запись ϕ = arctg a озна

чает, что ϕ (− 2π ; 2π ) и tg ϕ = a, то все гда выполняется равенство

tg (arctg a) = a .

Эту формулу можно не запоми нать: достаточно обозначить выра# жение в скобках через ϕ и применить определение арктангенса.

153

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
13.4. ФУНКЦИЯ y = arcctg x
				Т а б л и ц а 29
		1. График
y = ctg x			y = arcctg x
На промежутке (0; π) ctg x убывает.
	2. Значение arcctg a
Ориентир				Пример
arcctg a — это такое число из про				3 = π , так как
межутка (0; π), котангенс которого			arcctg
равен а.				6
			π (0; π) и ctg π =
ϕ (	0;	π)			3.
		,	6	6
arcctg a = ϕ, если ctgϕ = a
3. Формула для arcctg (–a)
			arcctg (–a) = π – arcctg a
Объяснение и обоснование

1. График функции y = arcctg x. Функция y = ctg x убывает на промежутке (0; π) и принимает все значения от –× до +×. Таким образом, на этом проме жутке функция y = ctg x имеет обратную функцию, которая обозначается y = arcctg x, с областью определения (–×; +×) и областью значений (0; π). Функция y = arcctg x также убывает, и ее график можно получить из графика

154

§ 13. Обратные тригонометрические функции

Рис. 92

Рис. 93

функции y = ctg x (на заданном промежутке) с помощью симметричного отоб ражения его относительно прямой y = x (рис. 92).

2. Значение arcсtg a. По определению обратной функции (на выбранном про межутке), если ctg ϕ = a, то arcctg a = ϕ, причем ϕ (0; π). Таким образом, запись arcctg a = ϕ означает, что ϕ (0; π) и ctg ϕ = a. То есть

arcctg a — это такое число из промежутка (0; π), котангенс которого равен a.

Например, arcctg 1 = π , поскольку							π	(0; π) и ctg			π	= 1.
	4				4						4
			3		2π				2π	(0;	π ) и ctg		2π		3
Аналогично arcctg	−			=		, поскольку								= −		.
			3		3				3		3				3

3. Формула для arcctg (–a). Для нахождения арккотангенсов отрицатель ных чисел можно также пользоваться формулой arcctg (–a) = π – arcctg a.

(Это следует из того, что точки a и (–a) на линии котангенсов (рис. 93)

являются симметричными относительно оси Оy. Тогда и соответствующие точки A и B на единичной окружности (на промежутке (0; π)) также будут симметричными относительно оси Оy. Таким образом, COA = DOB, значит, COB = π – DOB = π – COA.

Но arcctg a = COA, а arcctg (–a) = COB = π – COA. Получаем

arcctg (–a) = π – arcctg a . )

Например, arcctg (−1) = π − arcctg1 = π − π = 3π .

4 4

Отметим, что равенство arcctg (–a) = π – arcctg a означает, что функция y = arcctg x не является ни четной, ни нечетной.

155

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

Задача 1 Найдите ctg (arcctg 7).

Р е ш е н и е

X Пусть arcctg 7 = ϕ, тогда по опре делению арккотангенса получаем, что ctg ϕ = 7.

Таким образом,

ctg (arcctg 7) = ctg ϕ = 7. Y

К о м м е н т а р и й

Поскольку запись ϕ = arcctg a означает, что ϕ (0; π) и ctg ϕ = a, то всегда выполняется равенство

ctg (arcctg a) = a .

Эту формулу можно не запоми нать: достаточно обозначить выра# жение в скобках через ϕ и применить определение арккотангенса.

Докажите, что arctg a + arcctg a =

π

.

Задача 2*

2

Р е ш е н и е

К о м м е н т а р и й

X Пусть ϕ = π − arcctg a.

Запишем заданное равенство в виде

2

π

1) Поскольку arcctg a (0; π), то

arctg a =

− arcctg a . Если обозна

ϕ (−

π

π

).

2

;

π

чить ϕ =

− arcctg a, то для доказа

2

2

2) Если arcctg a = β,

2

тельства равенства arctg a = ϕ по оп

то ctg β = a и ϕ =

π

− β. Тогда

ределению арктангенса достаточно

2

доказать, что:

tgϕ = tg(

π

− β)= ctgβ = a.

π

π

2

По определению арктангенса полу

1) ϕ (−

2

;

2

) и 2) tg ϕ = a.

При доказательстве следует также

чаем arctg a = ϕ.

Таким образом, arctg a = π − arcctg a,

учесть определение арккотангенса:

если

а это и означает, что

2

arcctg a = β, то

arctg a + arcctg a =

π

. Y

β (0; π) и ctg β = a.

2

Вопросы для контроля

1.Объясните, какое число обозначает выражение: а) arcsin a; б) arccos a; в) arctg a; г) arcctg a. При каких значениях a существуют эти выражения? Проиллюстрируйте объяснение примерами.

2.Объясните, как можно получить графики обратных тригонометрических функций.

156

§ 13. Обратные тригонометрические функции

3*. Изобразите графики обратных тригонометрических функций, укажите и

	обоснуйте их простейшие свойства (область определения, множество зна
	чений, возрастание или убывание, четность, нечетность):
	а) y = arcsin x;														б) y = arccos x;											в) y = arctg x;																			г) y = arcctg x.
4.	Обоснуйте формулы:
	а) arcsin (–a) = –arcsin a;																									б) arctg (–a) = –arctg a;
	в) arccos (–a) = π – arccos a;																									г) arcctg (–a) = π – arcctg a.
	Упражнения
	Вычислите (1–9).
1°.	1) arcsin 0;														2) arcsin 1;											3)			arcsin			2		;
																													2
				3																													2
	4)	arcsin					;								5) arcsin (–1);											6)			arcsin −														.
				2
																																2														4) arctg(−		3).
2°.	1) arctg 0;														2) arctg 1;											3)			arctg 3;
3°.	1) arccos 0;														2) arccos 1;											3)			arccos			2			;
																																2
				3																														2
	4)	arccos				;									5) arccos (–1);											6)			arccos −														.
				2																												2
4°.	1) arcctg 0;														2) arcctg		3	;								3)			arcctg			3;														4) arcctg(−		3 ).
																3
5.	1)	sin(arcsin							2			);			2*)	cos(arcsin					1			);			3*) tg(arcsin									1				);						4*)	ctg(arcsin		4		).
				7												5																4																5
6.	1) tg (arctg 7);														*	ctg(arctg			1			);				3		*	) sin (arctg 3);																	*	(	)
															2 )	3																														4 )	cos arctg 2 .
7.	1)	cos(arccos								2			);		2*)	sin(arccos					1			);			3*) tg(arccos										3				);					4*)	ctg(arccos			1		).
				7												3																5																5
8.	1)	ctg(arcctg 7 );													2*) tg(arcctg					2			);				3*) sin (arcctg 5);																			4*) cos(arcctg				3			).
																				3																														4
9*.	1)	arcsin(sin						15π						);	2) arcsin (sin 7);											3)			arccos(cos										21π					);		4) arccos (cos 8);
								7																														5
	5)	arctg(tg			6π						);				6) arctg (tg 4);											7)			arcctg(ctg										10π						);	8) arcctg (ctg 10).
				5																																					9
10*. Докажите, что arcsin a + arccos a =																											π		при | a | m 1.
																										2

157

	§14	РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ
		УРАВНЕНИЙ
	Простейшими тригонометрическими уравнениями называют уравнения
			cos x = a, sin x = a, tg x = a, ctg x = a.
	Чтобы рассуждения по нахождению корней этих уравнений были более
	наглядными, воспользуемся графиками соответствующих функций.
	14. 1. УРАВНЕНИЕ cos x = a
					Т а б л и ц а 30
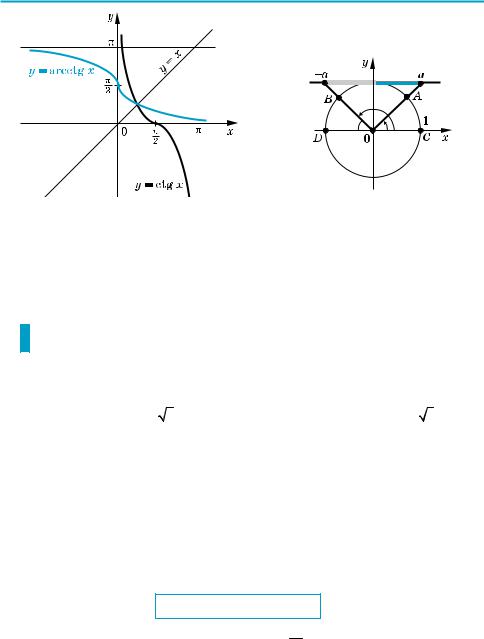
	1. Графическая иллюстрация и решение уравнения cos x = a
			Графическая иллюстрация
		Решения		Примеры
		cos x = a		1. X cosx = 1 ,
					2
	| a | > 1		| a | m1	x = ± arccos 1 + 2πn, n Z,
					2
	Корней нет			x = ± π + 2πn, n Z. Y
				3
	х = ä arccos a + 2πn, n Z			2. X cosx =	3.
				Корней нет, поскольку 3 > 1. Y
			2. Частные случаи решения уравнения cos x = a
				cos x = 0	x = π + πk, k Z
					2
				cos x = 1 x = 2πk, k Z
				cos x = –1 x = π + 2πk, k Z
				158

§ 14. Решение простейших тригонометрических уравнений

Объяснение и обоснование

1. Корни уравнения cos x = a. При | a | > 1 уравнение не имеет корней, по скольку | cos x | m 1 для любого x (прямая y = a на рисунке из пункта 1 табли цы 30 при a > 1 или при a < –1 не пересекает график функции y = cos x).

Пусть | a | m 1. Тогда прямая у = а пересекает график функции у = cos х. На промежутке [0; π] функция y = cos x убывает от 1 до –1, поэтому уравнение cos x = a имеет только один корень x 1 = arccos a на этом промежутке (рис. из пункта 1 табл. 30).

Косинус — четная функция, поэтому на промежутке [–π; 0] уравнение cos x = a также имеет только один корень — число, противоположное x1, то

есть x2 = –arccos a.

Таким образом, на промежутке [–π; π] (длиной 2π) уравнение cos x = a при | a | m 1 имеет только корни x = ä arccos a.

Функция y = cos x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных на 2πn (n Z). Получаем следующую форму

лу корней уравнения cos x = a при | a | m 1:
x = ä arccos a + 2πn, n Z .	(1)

2. Частные случаи решения уравнения cos x = a.

(Полезно помнить специальные записи корней уравнения cos x = a при a = 0, a = –1, a = 1, которые можно легко получить, используя как ориентир единичную окружность.

Поскольку косинус равен абсциссе соответствующей точки единичной ок ружности, получаем, что cos x = 0, если соответствующей точкой единич ной окружности является точка A или точка B (рис. из пункта 2 табл. 30). Тогда

x = 2π + πk, k Z.

Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно, x = 2πk, k Z. Также cos x = –1 тогда и только тогда, когда соответствующей точкой еди ничной окружности является точка D, таким образом, x = π + 2πk, k Z. )

Примеры решения задач

Решите уравнение cosx = −

1

.

Задача 1

2

Р е ш е н и е

К о м м е н т а р и й

X x = ± arccos(−

1

)+ 2πn, n Z,

Поскольку

−

1

<1, то данное урав

2

2

x = ± (π −

π

)+ 2πn,

нение вида cos x = a имеет корни, ко

торые можно найти по формуле (1).

3

159

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

2π

)мож

1

x = ±

+ 2πn.

Для вычисления arccos(−

3

2

Ответ: ±

2π

+ 2πn, n Z. Y

но воспользоваться формулой:

arccos (–a) = π – arccos a.

3

Тогда

arccos(−

1

)= π − arccos(

1

)= π −

π

=

2π

.

2

2

3

3

Решите уравнение cosx = 2.

Задача 2

Р е ш е н и е

К о м м е н т а р и й

X Поскольку

2

> 1, то корней

Поскольку

2

>1, то данное урав

нет.

нение не имеет корней (то есть фор

Ответ: корней нет. Y

мулу (1) нельзя применить).

1

Решите уравнение cos 4x =

.

Задача 3

3

Р е ш е н и е

X 4x = ± arccos 1 + 2πn, n Z,

3

x = ±	1	arccos	1	+		πn		, n Z.
4		3			2
Ответ:
± 1 arccos 1					+		π n		, n Z. Y
4				3	2

К о м м е н т а р и й

Поскольку 1 <1, то можно вос

3

пользоваться формулой (1).

Учитывая, что arccos 1 не является

3

табличним значением, для получен ния ответа достаточно после нахож дения 4х по формуле (1) обе части по следнего уравнения разделить на 4.

З а м е ч а н и е. Если по условию задания необходимо найти приближенное значение корней данного уравнения на каком то промежутке, то с помощью

калькулятора находим	1	arccos	1	≈ 0,31,	π	≈ 1,57,	записываем приближенное
	4				2
		3

значение корней в виде x ≈ ä 0,31 + 1,57п, n Z, находим приближенное значение корней при п = 0, ä1, ä2... и выбираем корни, входящие в данный промежуток.

		Решите уравнение cos (2x −					π	)=	2	.
	Задача 4
							3		2
		Р е ш е н и е							К о м м е н т а р и й
	X 2x − π = ± arccos		2	+ 2πn, n Z,		Поскольку						2		<1, то можно вос
											2
	3	2
					пользоваться формулой (1) для на

160

	§ 14. Решение простейших тригонометрических уравнений
	2x − π = ± π + 2πn,			хождения значения выражения
		3	4	2x − 3π, стоящего под знаком косину
	x = π ± π + πn, n Z.
	6	8		са. После этого из полученного линей
	Ответ: π ± π + πn, n Z. Y
				ного уравнения находим х.
	6	8
	14.2. УРАВНЕНИЕ sin x = a
					Т а б л и ц а 31
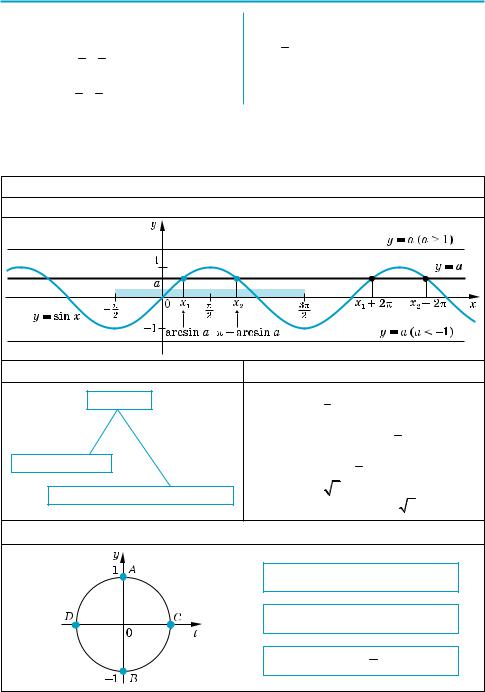
	1. Графическая иллюстрация и решения уравнения sin x = a
			Графическая иллюстрация
		Решения			Примеры
		sin x = a		1. X sinx = 1 ,
				2
	| a | > 1		| a | m 1	x = (−1)n arcsin 1 + πn, n Z.
					2
	Корней нет				n π
				x = (−1) 6 + πn, n Z. Y
	x = (–1)n arcsin a + πn, n Z			2. X sinx =	3.
				Корней нет, так как 3 > 1. Y
		2. Частные случаи решения уравнения sin x = a
				sin x = 0 x = πk, k Z
				sin x = 1	x = π + 2πk, k Z
					2
				sin x = –1	x = − π + 2πk, k Z
					2
				161