Методы оптимизации / volsu419

1, x& = uˆ =

−1

Из x(±π) = 0 следует

t +π,

xˆ = − t,

t −π,

−π ≤ t < −π 2 , π 2 ≤ t < π .
−π 2 ≤ t < π 2
−π ≤ t ≤ π 2
t ≤ π 2	,
π 2 ≤ t ≤ π

π			π	π				π		π
						π		&		&
B = ∫hsin t dt = ∫hp dt = ∫h dp = hp |−π							−∫hp dt = −∫hp dt ≥ 0 .
		&
−ρ		−π		−π				−π		−π
	&	&		p ≥	&		&	≤ 0
Так как			≤1,		0 xˆ	=1 h				.
	xˆ	+ h			&			&
				p ≤ 0 xˆ = −1 h ≥					0
Отсюда xˆ abs min .
Для решения задачи на max полагаем λ0							= −1 . Получаем практи-

чески предыдущую задачу с решением − xˆ , где xˆ − решение на минимум. Итак, − xˆ abs max .

2			x ≤ 2,		x(0) = x(0) = x(2) = 0 .
Пример 2. ∫x dt → extr,
0			&&				&	&
&	&&	= u и приведём задачу к виду (P):
Положим x1 = x, x2 = x, x
2	x1	= x2 ,			x2 = u, u [−2, 2],
B(x) = ∫x1dt → min,
	&				&
0
x1 (0) = x2 (0) = x2 (2) = 0.
Функция Лагранжа
2
Λ = ∫(λ0 x1 + p1 (t)(x1 − x2 ) + p2 (t)(x2 − u)dt +
&					&
0
+ λ1 x1 (0) + λ2 x2 (0) + λ3 x2 (2) .
Необходимые условия:
а) уравнения Эйлера
− p1 + λ0 = 0 p1 (t) = λ0t + C1
&							2 + C1t + C2
− p2 − p1 = 0 p2 (t) = −λ0 t						2
&
		41

б) трансверсальности

p1 (0) = λ1 ,

p1 (2) = 0

p

2

(0) = λ

,

p

2

(2) = −λ ;

2

3

в) оптимальности по u

sgn p2 (t),

p2 (t) ≠ 0

min− p2 (t)u = −p2 (t)uˆ(t) uˆ =

u ≤2

любоечисло из[−2, 2]

г) λ0 ≥ 0 .

а)

б)

а)

в)

λ0 = 0 p1

= C1 p1

= 0

p2

= C2 ≠

0 uˆ

= −2 или

&&

или 2 x

2

= t

2

+ A1t + A2

или

x = −t

2

+ B1t

+ B2 .

2 x = −2

&

&

= 0 λ0 ≠ 0 . Пусть

Для этих x не выполняется x(0) = x(0) = x(2)

a )

λ0 =1 p1 (t) =

б)

а)

(t) = −(t − 2)2

2 + C − парабола ветвя-

= t + C p (t) = t − 2 p

2

1

ми вниз с осью симметрии x = 2. Если она не меняет знак, то как показано выше, получается x, не удовлетворяющий конечным условиям. Поэтому

парабола меняет знак с "−" на "+" на [0, 2].

Следовательно,

&&

− 2, 0 < t

<τ

&

− 2t + C1

, 0

< t <τ

.

uˆ = xˆ

=

τ < t

2

xˆ =

< t < 2

2,

<

2t + C2 ,

τ

x&(0) = x&(2) =

&

=

− 2t,

0 < t <τ

.

0 xˆ

τ < t < 2

2t − 4,

Из непрерывности xˆ

в точке τ :

− 2τ = 2τ − 4 τ =1 xˆ =

− t2 + C1

,

0 ≤ t ≤

1

,

t2 − 4t + C2 , 1 ≤ t ≤

2

x(0) = 0 C1 = 0 .

Из непрерывности xˆ

в точке τ =1 C2 = 2.

− t

2

,

0 ≤ t ≤1.

Имеем xˆ =

t2

− 4t + 2, 1 ≤ t ≤ 2

42

		2				2	2			2		2
	B = ∫(xˆ + h)dt − ∫xˆdt = ∫hdt = −∫ &p&2 gdt = −∫h dp&2 =
		0				0	0			0		0
					2		2			2			2
		2			&		&	&	2	&&			&&
= −hp2 |0					+∫h dp2 = ∫h dp2			= hp2	|0	−∫hp2		dt = −∫hp2 dt ≥ 0 .
&
					0		0			0			0
										&		&	= 0 ).
(Здесь используются: h(0) = p2 (2) = h(0)											= h(2)
								&
	&xˆ&+ h&&			≤ 2,		p2 ≤ 0 &xˆ&= −1 h&&≥ 0
						p2 ≥ 0 &xˆ&=1 h&&≤ 0 .

Отсюда xˆ abs min .

Вследствие симметричности условий задачи при λ0 = −1 получаем

− xˆ abs max .

13.Задачи

1.x12 + x22 − 3x1 x2 → extr .

2.2x14 − x24 − x12 − 2x22 → extr .

3.

5x

2 + 4x x

2

+ x2 −16x

−12x

2

→ extr .

1

1

2

1

4.

5x2 + 4xy + y2 → extr,

x + y =1.

5.

x

+ 2x

2

+ 3x

3

→ extr,

x2

+ x

2

+ x2

=1.

1

1

2

3

6.

x2 + y2

→ extr,

3x + 4 y =1 .

7.

x2

+ x2

+ x2

→ extr,

x

+ x

2

+ x

3

=1,

x + x

2

− x

3

=1 2 .

1

2

3

1

1

x2

+ x2

+ x2

→ extr,

x

+ x

+ x

≤12,

x

≥ 0,

i =

.

8.

2

3

i

1, 3

1

2

3

1

9.

x1 x2 − 2x2

→ extr, 2x1 − x2

− 3x3 ≤10, x2

≥ 0, 3x1 + 2x2 + x3

= 6

.

10.

ex1 −x2 − x − x

2

→ extr,

x

+ x

2

≤1,

x

≥ 0,

x

2

≥ 0 .

1

1

1

11.

z = x1 + x2

→ max, x1 + 2x2

≤1,

3x1 + x2

≤ 2,

xi

≥ 0,

i =1, 2 .

12.

z = x1 + 3x2

+ 5x3

→ max,

2x1 + x2

+ x3

≥1,

x1 − x2 + 2x3

≤1,

x1 + 2x2 − 3x3 ≥ 2, xi ≥ 0, i =1, 3 . 43

Взадачах 13 - 15 найти производную Фреше.

13.f : C[0, 1] → R, f (x( )) = sin(x(1)) .

14.f : C[0, 1] → R, f (x( )) = sin x(0) cos x(1) .

																									1					3
15.	f : C[0, 1] → R,																f (x( )) =								∫x		2
																													(t) dt .
																									0
	T0
16.	∫			&		2			− x) dt → extr,												x(0) = 0,								x(T0 ) = ξ .
		(x
	0
	1
17.	∫			&		2		+ tx) dt → extr,													x(0) = x(1) = 0 .
		(x
	0
	e		&2				dt → extr,										x(1)				= 0,			x(e)				=1.
18.
	∫tx
	0
	1										2	dt → extr,									x(0) = 0,								x(1) =1 .
19.										&
	∫(1 + t) x
	0
	1
20.	∫x			2			&	2		dt → extr, x(0) =1,															x(1) =					2 .
						x
	0
	π 2				&2						2											2				2
21.									− x			− 2x) dt −									2x		(0)	− x				(π 2) → extr .
	∫(x
	0
	1	&2				dt + 4x							2	(0) −5x					2		(1) → extr .
22.
	∫x
	0
	1			&		2										x	2 (1)
23.	∫	(x						− x) dt −												→ extr .
																	2
	0
24.	1	(x1 x2 + x1 x2 ) dt + x1 (0)x2 (1) + x1 (1)x2 (0) → extr .
	∫
				&			&
	0
	2
25.	∫t		2		&2				dt − 2x(1)								+ x → extr .
					x
	1
																								44

T

&2	dt → extr, x(0)	= 0, T + x(T ) +1 = 0 .
26. ∫x
0

T

27. ∫

0

1

28. ∫

0

1

29. ∫

0

π

30. ∫

0

π

31. ∫

0

1

32. ∫

0

&

2

+ x) dt → extr,

x(0) =1 .

(x

&2

dt − 2x

2

(1)

→ extr,

x(0) = 0 .

x

&

2

+ x) dt → extr,

x(1) = 0 .

(x

π

π

&2

dt → extr,

∫x cos t dt =

,

x(0) =1,

x(π) = −1.

x

2

0

π

&2

dt → extr,

∫x sin t dt = 0,

x(0) = 0,

x(π) =1.

x

0

&

2

+ x

2

) dt → extr,

1

t

dt

=

e

2 +

1

,

x(0) = 0, x(1) = e .

(x

∫xe

4

0

	2								2			7
33.	∫t	2	&		2	dt → extr,			∫tx dt =				, x(1) =1,	x(2) = 2 .
			x									3
	1								1
	1								1
34.	&2			dt → extr,					∫x	2	dt =1,		x(0) = x(1)	= 0 .
	∫x
	0								0
	1
35.	&&2			dt → extr,							&		&	x(1) =1.
	∫x								x(0) = x(0)				= x(1) = 0,
	0
	π	&&2					2
36.					− x			) dt → extr, x(0) =					&	&
	∫(x												0, x(0) =1, x(π) = shπ, x(π) = chπ
	0
	.
	π	&&2					2
37.					− x								&	&
	∫(x							)dt → extr, x(0) = x(0) = 0, x(π) = shπ, x(π) = chπ +1
	0

45

	1
38.	&&2		+4x	2				&	&	=chπ
	∫(x					)dt →extr, x(0) =−1, x(0) =0, x(π) = shπ, x(π)
	0
	1
39.	&&2		&2		)dt →extr, x(0) =			&	&	= sh1
	∫(x		+ x					1, x(0)	= 0, x(1) = ch1, x(1)
	0
	T						T
40.	&2	dt → extr,					∫x dt =1,	x(0) = 3 .
	∫x
	0						0
	T						T
41.	&2	dt → extr,					∫x dt =1 3,	x(T ) =1.
	∫x
	0						0

ππ

42.

&2

dt → extr,

∫x sin t =1,

x(0) = 0 .

∫x

0

0

1

43.

&&2

dt → extr,

&

&

∫x

x(0) = x(1) = 0,

x(0) =1 .

0

e

44.

∫t

2

&&2

dt → extr,

x(1) = −1,

&

= e .

x

x(e) = x(1)

1

45.

7π 4

x ≤1,

x(0) = 0 .

∫x sin t dt → extr,

0

&

4

2

+ x) dt → extr,

≤1,

x(4) = 0 .

46.

&

&

∫(x

x

0

47.

2

x ≤ 2,

x(0) + x(2) = 0,

x(0) = 0 .

∫x dt → extr,

0

&&

&

48.

4

x ≤ 2,

x(0) + x(4) = 0,

x(0) = x(4) = 0 .

∫x dt → extr,

0

&&

&

&

49.

2

x dt → min,

x ≥ −2,

x(0) = 0, x(2) = −1,

x(2) = −2 .

∫

0

&&

&&

50.

2

x dt → min,

x ≤ 2,

x(0) = 0,

x(2) =1, x(2) = 2 .

∫

0

&&

&&

&

46

14.Ответы

1.(1, 1) loc min, (0, 0) loc extr, Smin = −∞, Smax = ∞.

2.(±1/2, ±1) abs min, Smin = −9/8, (0, 0) loc max, (±1/2, 0), (0, ±1) loc extr, Smax = ∞.

3.(−4, 14) abs min, Smin = −52, Smax = ∞.

4.(−1/2, 3/2) abs min, Smax = ∞.

5. (1 14, 2 14, 3 14) abs min , Smin = −1071 2 , Smax = 2 .

6.(3/25, 4/25) abs min, Smin = 1/25, Smax = ∞.

7.(3/8, 3/8, 1/4) abs min, Smin = 11/32, Smax = ∞.

8.(0, 0, 0) abs min, Smin = 0, (12, 0, 0), (0, 12, 0), (0, 0, 12)

	abs max, Smax = 144; (4, 4, 4), (0, 6, 6), (6, 0, 6), (6, 6, 0) −
	критические точки в задаче на максимум.
9.	(2 7 ,174 35,−24 5) loc min, Smin = −∞ , (1, 0, 3) loc max,
	Smax = +∞, (−1, 6,−3) loc extr .
10.	(0,1) abs min, Smin = e−1 , (0,1) abs max ,
	Smax = e −1, (0, 0) loc extr .

11.zmax = 13 в точках (0, 0, 13), (2, 0, 11), (x1, 0, 13−x1) при x1 [0, 2].

12.zmax = 7/3 в точке (4/3, 1/3, 0).

13.f ′(xˆ( ))[h( )] = cos xˆ(1) h(1)

14.f ′(xˆ( ))[h( )] = cos xˆ(0) h(0) cos xˆ(1) −sin xˆ(0) sin xˆ(1) h(1) .

1

15.f ′(xˆ( ))[h( )] = 6 ∫0

16.− t2 4 + (ξ T0 +T0

			2	1
	xˆ	2		∫xˆ(t) h(t) dt .
			(t) dt
				0

4)t abs min, Smax = +∞.

17.(t3 − t)12 abs min, Smax = +∞.

18.ln t abs min, Smax = +∞.

19.(ln(t +1))ln 2 abs min, Smax = +∞.

20. t +1 abs min, Smax = +∞ .

21.cos t −1 loc extr, Smin = −∞(xn (t) ≡ n, Smax = +∞.

47

22.	xˆ ≡ 0 −единственная экстремаль,
	xˆ loc extr, Smin = −∞ (xn ≡ n), Smax = +∞ .
23.	− (t2 + 3) 4 loc extr, Smin = −∞ (xn (t) ≡ n), Smax = +∞ .
24.	(0,0) loc extr, Smin = −∞ (xn (t) = n,−n)), Smax = +∞ (xn (t) =
	= (n, n)) .
25.	1 t +1 2 abs min, Smax = +∞ .
26.			ˆ	=1) abs min, Smin = 4, Smax = +∞ .
	(xˆ = −2t, T
27.	(xˆ = (t	2	4)	ˆ	− t,
				− t +1, T = 2) loc extr, Smin = −∞(xn (t) =1

T n= n), Smax = +∞ .

28.0 loc extr, Smin = −∞ (xn (t) = nt), Smax = +∞ .

29.(t2 −1)4 abs min, Smax = +∞ .

30.cos t abs min, Smin = π2 , Smax = +∞.

31.(t − 2 sin t)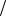π abs min, Smax = +∞.

32.tet abs min, Smax = +∞ .

33.t abs min, Smin = 73, Smax = +∞.

34.± 2 sinkπt, k Ν, ± 2 sinπt absmin,Smin =π2 , Smax = +∞.

35.− 2t3 + 3t2 abs min, Smin =132, Smax = +∞ .

36.sh t abs min, Smax = +∞.

37.sh t −sin t abs min, Smax = +∞ .

38.− ch t cos t abs min, Smax = +∞.

39.ch t abs min, Smax = +∞.

40.	− 1 −t2 abs min, Smin = −π 4,			1 −t2 abs max, Smax =π 4 .
41.	(xˆ =	ˆ	abs min, Smin = 0, (xˆ = t		2	ˆ	=1) loc extr,
		1, T =1 3)				, T
	Smax	= +∞ .

42.23π (t + sin t) abs min, Smax = +∞ .

43.− (t2 2) + t abs min, Smin =1, Smax = +∞ .

44.(t + e) ln t − t abs min, Smax = +∞ .

48

45.		− t,
	x =
	t −π 2 ,
46.		2	4) −
	x = (t
			t − 4,

0 ≤ t ≤ π 4,	4 ,	abs min, − xˆ	abs max .
π 4 ≤ t ≤ 7π

3, 0 ≤ t ≤ 2,	abs min, 4 −t abs max .
2 ≤ t ≤ 4,

47.	x = t2 − 2 abs min, Smin = −4 3, − xˆ abs max, Smax = 4 3 .
			− t2 ,			0 ≤ t ≤1,
48.	x =	(t − 2)2 − 2,				1 ≤ t ≤ 3,		abs min,		− xˆ abs max .
			− (t − 4)	2	,	3 ≤ t ≤ 4,
49.	x =		0,			0 ≤ t ≤1,	abs min, S			=1 .
									min
		− (t −1)2 , 1 ≤ t ≤ 2,

0, 0 ≤ t ≤1,

50.x = (t −1)2 , 1 ≤ t ≤ 2, abs min, Smin =1.

49

	СОДЕРЖАНИЕ
Введение..........................................................................................................		3
1.	Конечномерные гладкие задачи без ограничений................................	4
2.	Конечномерные гладкие задачи с ограничениями типа равенств.......	7

3.Конечномерные гладкие задачи с ограничениями типа равенств

	и неравенств .............................................................................................	11
4.	Линейное программирование .................................................................	16
5.	Производная Фреше ................................................................................	20
6.	Простейшая задача вариационного исчисления ...................................	22
7.	Задача Больца...........................................................................................	25
8.	Задача с подвижными концами ..............................................................	27
9.	Изопереметрическая задача....................................................................	29
10.	Задача со старшими производными.......................................................	32
11.	Задача Лагранжа.......................................................................................	33
12.	Задачи оптимального управления..........................................................	37
13.	Задачи........................................................................................................	42
14.	Ответы.......................................................................................................	46

50