Лекция 3 Линии второго порядка, заданные каноническими уравнениями
§ 112. Гипербола и ее каноническое уравнение
Определение. Гиперболой называется геометрическое место точек, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2а, меньшее, чем расстояние 2с между фокусами.
Пусть
-
произвольная точка гиперболы, а
и
- ее фокусы. Отрезки
и
так
же, как и их длины, называются фокальными
радиусами гиперболы. Поэтому
(1)
Введем
на плоскости прямоугольную систему
координат, принимая середину отрезка
за начало координат, а за ось Ох
– прямую
,
ориентированную от точки
к точке
.
В выбранной системе координат фокус
имеет координаты
,
а фокус
- координаты
.
Обозначая координаты точки М
гиперболы через
х
и у,
будим иметь
,
и
соотношение
принимает вид
Преобразуем
это уравнение. Раскрываем модуль
,
.
Дважды возводим в квадрат, получим:
Однако,
теперь
.
Обозначая разность
через
:
,
(2)
имеем:
,
или
(3)
Итак,
координаты любой точки гиперболы
удовлетворяют уравнению (3):
Докажем
обратное. Если координаты некоторой
точки М(х,
у)
удовлетворяют уравнению (3), то
Для
этого найдем расстояние
и
от этой точки до точек
и
:
и
аналогично
.
Из
равенства
Следует,
что
Если
,
то в силу соотношения
будем иметь
,
а потому
(4)
Если
же
,
то
а потому
(5)
Таким
образом, если
;
то
,
а если
,
то
,
в обоих случаях
.
Итак, мы доказали, что координаты любой точки гиперболы удовлетворяет уравнению
,
и обратно: если координаты точки удовлетворяют этому уравнению, то эта точка лежит на рассматриваемой гиперболе.
Следовательно, уравнение
является уравнением гиперболы: оно называется каноническим уравнением гиперболы.
§ 113. Исследование формы гиперболы
Так как
в каноническое уравнение гиперболы
координаты х
и у
входят во второй степени. То оси Ох
и Оу
являются осями симметрии гиперболы,
заданной уравнением:
.
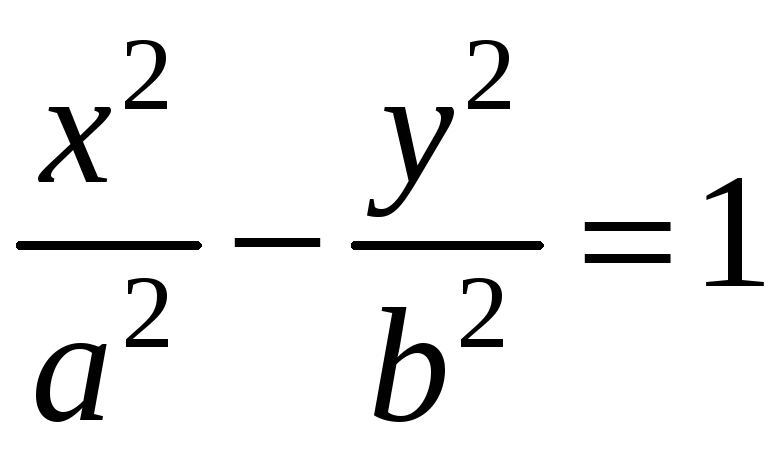(1)
а начало координат – центром симметрии.
Из уравнения (1) следует, что
,
т.е. или
,
или
.
Геометрически это означает, что между
прямыми
и
нет ни одной точки гиперболы (1).
Ось симметрии Оу не пересекает гиперболу, заданную уравнением (1), и называется мнимой осью. Ось Ох – пересекает гиперболу (1) в двух точках:
.
Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекается гиперболу, называются вершинами гиперболы.
Числа а и b в каноническом уравнении называются действительной и мнимой полуосями гиперболы.
Решая
уравнение (1) относительно у,
беря лишь положительное значение:
(2)
и считая
,
мы получим точки гиперболы (1), лежащие
в первой четверти. Из уравнения (2)
следует, что у
в полуинтервале
есть возрастающая функция; при этом
.
Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением первой степени, а гипербола – второй.
Рассмотрим
уравнение прямой
(3)
Найдем
расстояние
от точки М(х,
у),
лежащей на дуге гиперболы, определяемой
уравнением (2), до прямой (3); переписывая
уравнение (3) в виде
,
находим:
Отсюда
следует, то на полуинтервале
расстояние
от точки М(х,
у)
рассматриваемой части гиперболы до
прямой (3) есть убывающая функция от х
и
(рис. 167). Прямая, определяемая уравнением
называется асимптотой гиперболы.
В силу
того, что гипербола, заданная каноническим
уравнением, симметрична относительно
начала координат, расстояние от точки
М(х,
у),
лежащей на дуге гиперболы, заданной
уравнением
до прямой
стремиться к нулю при
.
Так как гипербола, заданная каноническим
уравнением, симметрична и относительно
оси Оу,
то она имеет вторую асимптоту
,
которая обладает свойством, аналогичным свойству первой асимптоты по отношению к дугам гиперболы, расположенным во второй и четвертой четвертях.
Асимптоты
гиперболы являются диагоналями
прямоугольника
,
,
,
.
При
одной и той же абсциссе х
ординаты точки ветви гиперболы, лежащей
в первой четверти, с ординатой точки
асимптоты
связаны неравенством:
.
Отсюда
и из того, что гипербола симметрична
относительно осей координат, следует,
что она имеет две ветви, заключенные в
двух областях: одна из них ограничена
отрезком
и продолжениями отрезков
и
за точки
и
,
другая симметрична этой области
относительно мнимой оси гиперболы (рис
168).
Рис.168
Гипербола, у которой полуоси равны, называются равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид
Уравнение асимптот равносторонней гиперболы таковы:
.
это биссектрисы углов между ее осями симметрии. Асимптоты равносторонней гиперболы взаимно перпендикулярны.
Обратно, если асимптоты гиперболы взаимно перпендикулярны, то ее полуоси равны между собой и, значит гипербола равносторонняя.