Лекция 2.11

Интервальные оценки.

Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема (n ≈ 100) точность таких оценок обычно бывает достаточной для практических выводов (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема (n ≈ 15 ÷ 40) это не так, и вопрос точности оценок становится очень важным.

Метод доверительных интервалов позволяет указать точность найденных оценок. Но при этом потребуется выполнение дополнительных условий.

Введем понятие интервальной оценки неизвестного параметра генеральной совокупности (или случайной величины , определенной на множестве объектов этой генеральной совокупности). Обозначим этот параметр θ. По сделанной выборке в соответствии с определенными правилами найдем числа θ ₁ и θ ₂, так чтобы выполнялось условие:

P(θ ₁< θ < θ ₂) =P (θ ( θ ₁; θ ₂)) = 

Числа θ₁ и θ₂ называются доверительными границами, интервал (θ ₁, θ ₂) — доверительным интервалом для параметра θ. Число  называется надежностью сделанной оценки.  принято выбирать равной 0,95, 0,99 или 0,999. Т. е. вероятность того, что значение интересующего нас параметра попало в интервал (θ ₁, θ ₂) достаточно высока. Число (θ ₁ + θ ₂)/2 — середина доверительного интервала будет давать значение параметра θ с точностью δ = (θ₂ – θ₁)/2, которая представляет собой половину длины доверительного интервала.

Границы θ₁ и θ₂ определяются из выборочных данных и являются функциями от случайных величин x₁, x₂, ..., x_n , и, следовательно, сами случайные величины. Поэтому доверительный интервал (θ₁, θ₂) тоже случаен. Он может покрывать или не покрывать неизвестное значение параметра θ. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число θ.

Наиболее часто в практике встречаются нормально распределённые случайные величины, поэтому будем строить доверительные для параметров нормального распределения — математического ожидания a, дисперсии σ² и среднего математического отклонения σ.

Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.

Дано: случайная величина  распределена по нормальному закону, для которого известна дисперсия  ².

Делается выборка объема n. Вычисляем . Покажем, что M 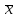= a и D=.

Выборка x₁, x₂, ..., x_n рассматривается как совокупность n независимых случайных величин, распределенных так же как , следовательно,

Mx₁ = Mx₂ = ... = Mx_n = а Dx₁ = Dx₂ = ... = Dx_n = σ².

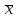также случайная величина и распределена по нормальному закону в силу теоремы — сумма нормально распределённых случайных величин распределена по нормальному закону.

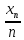М=М () = M ( + + … + ) = M () + M () + … + M () = M () = ^. n ^. a = a

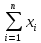D= D ( ) = = = ^. n ^. σ² = .

Итак, → N (a; ) .

Подберем по заданной надежности  число δ > 0 так, чтобы выполнялось условие:

P( – a < δ ) = . (1)

Так как случайная величина распределена по нормальному закону с математическим ожиданием a и дисперсией  ²/n, получаем:

P(– a < δ) =P(a – δ < < a + δ) =

= + Ф – + Ф = 2Ф

2Ф = , Ф.

Обозначим = . Функция Ф(x) непрерывна и возрастает на интервале [ 0; +∞) от 0 до 0,5, поэтому для любого числа  [0;1] существует единственное число такое, что ( )=  / 2. Это число называют квантилем нормального распределения, и в конкретных примерах оно подбирается по таблицам нормального распределения функции Лапласа.

Теперь из равенства = определим значение : = . Окончательный результат получим, представив формулу (1) в виде:

P( < a < ) = .

Другими словами, с надежностью  доверительный интервал

( ; )

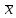
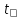
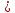
покрывает неизвестное значение параметр a = M генеральной совокупности. Можно сказать иначе: точечная оценка даёт значение параметра M с точностью = и надежностью .

Задача 1. Пусть имеется генеральная совокупность, распределенная по нормальному закону с дисперсией  ², равной 6,25. Произведена выборка объема n = 27 и получено средневыборочное значение = 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью  =0,99.

Решение. Сначала по таблице для функции Лапласа найдем значение из уравнения () =  / 2, () = 0,495. По полученному значению = 2,58 определим точность оценки = 2,52,58 /  1,24. Отсюда получаем искомый доверительный интервал:

θ ₁ = = 12 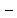1,24 = 10,76

θ₂ = = 12 1,24 = 13,24, (10,76; 13,24).

Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.

Пусть  – случайная величина, распределенная по нормальному закону с неизвестным математическим ожиданием a . Произведем выборку объема n. Вычислим среднюю выборочную и исправленную выборочную дисперсию s² .

Случайная величина t = ( a) / s распределена по закону Стьюдента с (n – 1) степенями свободы.

Задача заключается в том, чтобы по заданной надежности  и по числу степеней свободы (n – 1) найти такое число t_,n , чтобы выполнялось равенство

P(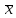(– a) / s < t_,n) =  (2)

или эквивалентное равенство

P(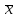 – t_,n s / < a < + t_,n s / ) = . (3)

Здесь в скобках написано условие того, что значение неизвестного параметра a принадлежит некоторому промежутку, который и является доверительным интервалом. Его границы зависят от надежности  , а также от параметров выборки Его границы зависят от надежности  и параметров выборки и s.

Чтобы определить значение t_ по величине , равенство (2) преобразуем к виду: P(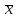(– a) / s ≥ t_,n) = 1 –  . Теперь по таблице для случайной величины t, распределенной по закону Стьюдента, по вероятности (1 – ) и числу степеней свободы (n – 1) находим t_,n . Формула (3) дает ответ на поставленную задачу.

Задача 2. На контрольных испытаниях 20-и электроламп средняя продолжительность их работы оказалась равной 2000 часов при среднем квадратическом отклонении, рассчитанном как корень квадратный из исправленной выборочной дисперсии, равном 11-и часам. Известно, что продолжительность работы лампы является нормально распределенной случайной величиной. Определить с надежностью 0,95 доверительный интервал для математического ожидания этой случайной величины.

Решение. Величина (1 – ) в данном случае равна 0,05. По таблице распределения Стьюдента при числе степеней свободы, равном 19, находим: t_,n = 2,093. Вычислим теперь точность оценки: = 2,09311 / = 5,14. Отсюда получаем искомый доверительный интервал (1994,9; 2005,1).

Доверительный интервал для дисперсии и среднего квадратического отклонения нормального распределения.

Пусть случайная величина  распределена по нормальному закону, для которого дисперсия D неизвестна. Делается выборка объема n. Определяется исправленная выборочная дисперсия s². Из теории известно, что границами доверительного интервала дисперсии являются

θ₁ = , θ₂ = , где ₁² и ₂² определяются по таблице распределения ² с (n – 1) степенями свободы как решения уравнений

P(² ≥ ₁²) = и P(² ≥ ₂²) = .

Отсюда легко получить формулу, по которой находится доверительный интервал для стандартного отклонения σ:

P( < σ_ < ) = .

Задача 3. Будем считать, что шум в кабинах вертолетов одного и того же типа при работающих в определенном режиме двигателях — случайная величина, распределенная по нормальному закону. Случайным образом выбрано 20 вертолетов, и произведены замеры уровня шума в каждом из них. Исправленная выборочная дисперсия измерений оказалась равной 22,5 децибела. Найти доверительный интервал, накрывающий неизвестное стандартное отклонение величины шума в кабинах вертолетов с надежностью 98%.

Решение. По числу степеней свободы, равному 19, и по вероятности (1 – 0,98)/2 =0,01 находим из таблицы распределения ² величину ₂² = 36,2. Аналогичным образом при вероятности (1 + 0,98)/2 = 0,99 получаем ₁² = 7,63. Выпишем искомый доверительный интервал: (3,4; 7,5).