
- •2. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея. Второй и третий законы Ньютона.
- •3. Центр масс механической системы. Закон движения центра масс. Движение центра масс замкнутой системы. Закон сохранения импульса.
- •4. Работа силы и ее выражение через криволинейный интеграл. Мощность.
- •5.Кинетическая энергия системы. Связь изменения кинетической энергии и работы.
- •6.Консервативные и неконсервативные силы. Сила тяжести, сила упругости, центральные силы как консервативные силы.
- •8.Полная механическая энергия системы, связь её изменения с работой неконсервативных сил. Закон сохранения полной механической энергии.
- •9. Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара.
- •Момент инерции
- •11.Основные уравнения динамики вращательного движения твердого тела.
- •12. Кинетическая энергия вращающегося твердого тела. Работа сил при вращательном движении тела. Кинетическая энергия твердого тела при плоском движении.
- •Кинетическая энергия при плоском движении
- •13.Гироскоп.Вывод формулы частоты прецессии гироскопа.
- •15.Сложение двух гармонических колебаний одинакового направления и частоты. Геометрическая интерпретация.
- •16.Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
- •17.Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
5.Кинетическая энергия системы. Связь изменения кинетической энергии и работы.
Кинетическая
энергия механической
системы - это энергия механического
движения рассматриваемой системы.
Сила F,
воздействуя на покоящееся тело и приводя
его в движение, совершает работу, а
энергия движущегося тела увеличивается
на величину затраченной работы. Значит,
работа dA силы F на
пути, который тело прошло за время
возрастания скорости от 0 до v, тратится
на увеличение кинетической энергии dT
тела, т. е.
![]() Используя
второй закон Ньютона
Используя
второй закон Ньютона ![]() и
умножая на перемещение dr получаем
и
умножая на перемещение dr получаем
![]() Так
как v=dr/dt,
то dA=mvdv,
откуда
Так
как v=dr/dt,
то dA=mvdv,
откуда
![]() Таким
образом, тело массой m, движущееся со
скоростью v, обладает кинетической
энергией
Таким
образом, тело массой m, движущееся со
скоростью v, обладает кинетической
энергией
![]() (1)
(1)
6.Консервативные и неконсервативные силы. Сила тяжести, сила упругости, центральные силы как консервативные силы.
![]()
![]()


7.Потенциальная энергия материальной точки во внешнем поле. Связь изменения потенциальной энергии и работы. Связь силы, действующей на материальную точку во внешнем поле, с её потенциальной энергией. Полная энергия материальной точки во внешнем поле и её изменение.

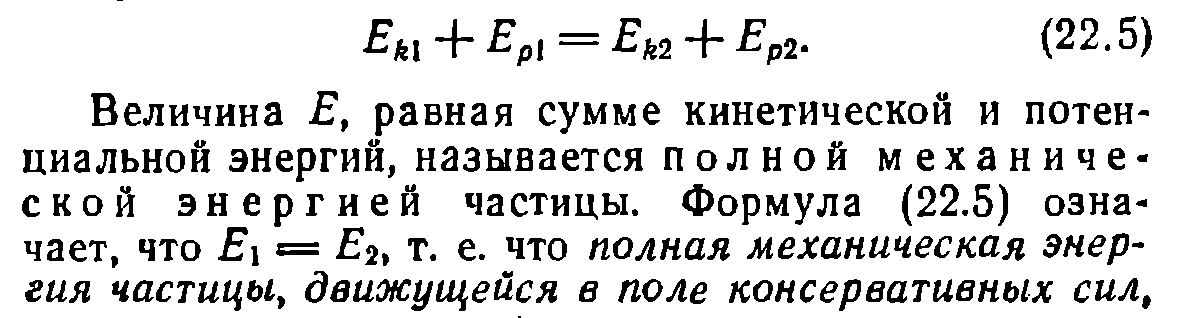
8.Полная механическая энергия системы, связь её изменения с работой неконсервативных сил. Закон сохранения полной механической энергии.


9. Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара.
Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу .
Если
массы шаров m1 и
m2,
их скорости до удара ν1 и ν2,
то, используя закон сохранения импульса
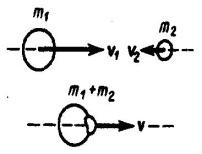
![]() где v -
скорость движения шаров после удара.
Тогда
где v -
скорость движения шаров после удара.
Тогда
![]() (15.10)
В
случае движения шаров навстречу друг
другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
(15.10)
В
случае движения шаров навстречу друг
другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
![]() Определим,
как изменяется кинетическая энергия
шаров при центральном абсолютно неупругом
ударе. Так как в процессе соударения
шаров между ними действуют силы, зависящие
от их скоростей, а не от самих деформаций,
то мы имеем дело с дисипативными силами,
подобным силам трения, поэтому закон
сохранения механической энергии в этом
случае не должен соблюдаться. Вследствие
деформации происходит уменьшение
кинетической энергии, которая переходит
в тепловую или другие формы энергии.
Это уменьшение можно определить по
разности кинетической энергии тел до
и после удара:
Определим,
как изменяется кинетическая энергия
шаров при центральном абсолютно неупругом
ударе. Так как в процессе соударения
шаров между ними действуют силы, зависящие
от их скоростей, а не от самих деформаций,
то мы имеем дело с дисипативными силами,
подобным силам трения, поэтому закон
сохранения механической энергии в этом
случае не должен соблюдаться. Вследствие
деформации происходит уменьшение
кинетической энергии, которая переходит
в тепловую или другие формы энергии.
Это уменьшение можно определить по
разности кинетической энергии тел до
и после удара:
![]() Используя
(10), получаем
Используя
(10), получаем
![]() Если
ударяемое тело было первоначально
неподвижно (ν2=0),
то
Если
ударяемое тело было первоначально
неподвижно (ν2=0),
то
![]() и
и
![]() Когда
m2>>m1 (масса
неподвижного тела очень велика),
то ν<<ν1 и
практически вся кинетическая энергия
тела переходит при ударе в другие формы
энергии. Поэтому, например, для получения
значительной деформации наковальня
должна быть значительно массивнее
молота. Наоборот, при забивании гвоздей
в стену масса молота должна быть гораздо
большей (m1>>m2),
тогда ν≈ν1 и
почти вся энергия тратится на возможно
большее перемещение гвоздя, а не на
остаточную деформацию стены.
Абсолютно
неупругий удар - это пример потери
механической энергии под действием
диссипативных сил.
Когда
m2>>m1 (масса
неподвижного тела очень велика),
то ν<<ν1 и
практически вся кинетическая энергия
тела переходит при ударе в другие формы
энергии. Поэтому, например, для получения
значительной деформации наковальня
должна быть значительно массивнее
молота. Наоборот, при забивании гвоздей
в стену масса молота должна быть гораздо
большей (m1>>m2),
тогда ν≈ν1 и
почти вся энергия тратится на возможно
большее перемещение гвоздя, а не на
остаточную деформацию стены.
Абсолютно
неупругий удар - это пример потери
механической энергии под действием
диссипативных сил.
Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай). Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса. Обозначим скорости шаров массами m1 и m2 до удара через ν1 и ν2, после удара - через ν1' и ν2' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.
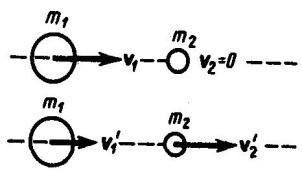
При
указанных допущениях законы сохранения
имеют вид
![]() (1)
(1)
![]() (2)
Произведя
соответствующие преобразования в
выражениях (1) и (2),
получим
(2)
Произведя
соответствующие преобразования в
выражениях (1) и (2),
получим
![]() (3)
(3)
![]() (4)
откуда
(4)
откуда
![]() (5)
Решая
уравнения (3) и (5), находим
(5)
Решая
уравнения (3) и (5), находим
![]() (6)
(6)
![]() (7)
Разберем
несколько примеров.
1.
При ν2=0
(7)
Разберем
несколько примеров.
1.
При ν2=0
![]() (8)
(8)
![]() (9)
Проанализируем
выражения (8) в (9) для двух шаров различных
масс:
а)
m1=m2.
Если второй шар до удара висел неподвижно
(ν2=0)
(рис. 2), то после удара остановится первый
шар (ν1'=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(ν2'=ν1);
(9)
Проанализируем
выражения (8) в (9) для двух шаров различных
масс:
а)
m1=m2.
Если второй шар до удара висел неподвижно
(ν2=0)
(рис. 2), то после удара остановится первый
шар (ν1'=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(ν2'=ν1);
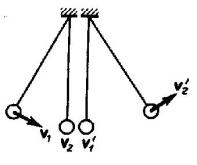
б) m1>m2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν1'<ν1). Скорость второго шара после удара больше, чем скорость первого после удара (ν2'>ν1' ) (рис. 3);
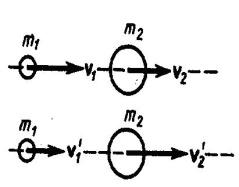
в) m1<m2. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν2'<ν1 (рис. 4);

г) m2>>m1 (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν1'= -ν1; ν2' ≈ 2m1ν2'/m2. 2. При m1=m2 выражения (6) и (7) будут иметь вид ν1'= ν2; ν2'= ν1; т. е. шары равной массы как бы обмениваются скоростями.
10.Момент импульса частицы относительно точки и относительно оси. Момент силы относительно точки и относительно оси. Законы изменения и сохранения момента импульс системы. Момент импульса твердого тела, вращающегося относительно неподвижной оси. Момент инерции тела относительно оси. Вычисление моментов инерции стержня, сплошного цилиндра. Теорема Гюйгенса-Штейнера. Закон сохранения момента импульса для вращательного движения.
Моментом
импульса (количества движения) материальной
точки А относительно неподвижной точки
О называется
физическая величина, определяемая
векторным произведением:
![]() где r -
радиус-вектор, проведенный из точки О
в точку A, p=mv -
импульс материальной точки (рис. 1); L -
псевдовектор, направление которого
совпадает с направлением поступательного
движения правого винта при его вращении
от r к р.
где r -
радиус-вектор, проведенный из точки О
в точку A, p=mv -
импульс материальной точки (рис. 1); L -
псевдовектор, направление которого
совпадает с направлением поступательного
движения правого винта при его вращении
от r к р.

Модуль
вектора момента импульса
![]() где
α - угол между векторами r и р, l -
плечо вектора р относительно
точки О.
Моментом
импульса относительно неподвижной оси
z называется
скалярная величина Lz,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки О
данной оси. Момент импульса Lz не
зависит от положения точки О на оси
z.
При
вращении абсолютно твердого тела вокруг
неподвижной оси z каждая точка тела
движется по окружности постоянного
радиуса riсо
скоростью vi .
Скорость vi и
импульс mivi перпендикулярны
этому радиусу, т. е. радиус является
плечом вектора mivi .
Значит, мы можем записать, что момент
импульса отдельной частицы равен
где
α - угол между векторами r и р, l -
плечо вектора р относительно
точки О.
Моментом
импульса относительно неподвижной оси
z называется
скалярная величина Lz,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки О
данной оси. Момент импульса Lz не
зависит от положения точки О на оси
z.
При
вращении абсолютно твердого тела вокруг
неподвижной оси z каждая точка тела
движется по окружности постоянного
радиуса riсо
скоростью vi .
Скорость vi и
импульс mivi перпендикулярны
этому радиусу, т. е. радиус является
плечом вектора mivi .
Значит, мы можем записать, что момент
импульса отдельной частицы равен
![]() (1)
и
направлен по оси в сторону, определяемую
правилом правого винта.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц:
(1)
и
направлен по оси в сторону, определяемую
правилом правого винта.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц:
![]() Используя
формулу vi =
ωri,
получим
Используя
формулу vi =
ωri,
получим
![]() т.
е.
т.
е. ![]() 2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени:
2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени:
![]() т.
е.
т.
е.
![]()
Эта
формула - еще одна форма уравнения
динамики вращательного движения твердого
тела относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси равна моменту сил относительно той
же оси.
Можно
показать, что имеет место векторное
равенство
![]() (3)
В
замкнутой системе момент внешних
сил
(3)
В
замкнутой системе момент внешних
сил ![]() и
и ![]() откуда
откуда
![]() (4)
Выражение
(4) представляет собой закон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т. е. не изменяется с течением
времени.
Закон
сохранения момента импульса также как
и закон сохранения энергии является
фундаментальным законом природы. Он
связан со свойством симметрии пространства
- его изотропностью,
т. е. с инвариантностью физических
законов относительно выбора направления
осей координат системы отсчета
(относительно поворота замкнутой системы
в пространстве на любой угол).
Здесь
мы продемонстрируем закон сохранения
момента импульса с помощью скамьи
Жуковского. Человек, сидящий на скамье,
вращающаяся вокруг вертикальной оси,
и держащий в вытянутых руках гантели
(рис. 2), вращается внешним механизмом с
угловой скоростью ω1.
Если человек прижмет гантели к телу, то
момент инерции системы уменьшится. Но
момент внешних сил равен нулю, момент
импульса системы сохраняется и угловая
скорость вращения ω2 увеличивается.
Аналогичным образом, гимнаст во время
прыжка через голову поджимает к туловищу
руки и ноги, с целью уменьшить свой
момент инерции и тем самым увеличить
угловую скорость вращения.
(4)
Выражение
(4) представляет собой закон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т. е. не изменяется с течением
времени.
Закон
сохранения момента импульса также как
и закон сохранения энергии является
фундаментальным законом природы. Он
связан со свойством симметрии пространства
- его изотропностью,
т. е. с инвариантностью физических
законов относительно выбора направления
осей координат системы отсчета
(относительно поворота замкнутой системы
в пространстве на любой угол).
Здесь
мы продемонстрируем закон сохранения
момента импульса с помощью скамьи
Жуковского. Человек, сидящий на скамье,
вращающаяся вокруг вертикальной оси,
и держащий в вытянутых руках гантели
(рис. 2), вращается внешним механизмом с
угловой скоростью ω1.
Если человек прижмет гантели к телу, то
момент инерции системы уменьшится. Но
момент внешних сил равен нулю, момент
импульса системы сохраняется и угловая
скорость вращения ω2 увеличивается.
Аналогичным образом, гимнаст во время
прыжка через голову поджимает к туловищу
руки и ноги, с целью уменьшить свой
момент инерции и тем самым увеличить
угловую скорость вращения.
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (см таблицы ниже).


Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 1):

![]() Здесь М -
псевдовектор, направление которого
совпадает с направлением поступательного
движения правого винта при его вращении
от r к F.
Модуль момента силы
Здесь М -
псевдовектор, направление которого
совпадает с направлением поступательного
движения правого винта при его вращении
от r к F.
Модуль момента силы
![]() (1)
где
α - угол между r и F;
rsinα=l -
наименьшее расстояние между линией
действия силы и точкой О - плечо
силы.
Моментом
силы относительно неподвижной оси
z называется
скалярная величина Mz ,
равная проекции на эту ось вектора М
момента силы, определенного относительно
произвольной точки О данной оси z (рис.
2).
(1)
где
α - угол между r и F;
rsinα=l -
наименьшее расстояние между линией
действия силы и точкой О - плечо
силы.
Моментом
силы относительно неподвижной оси
z называется
скалярная величина Mz ,
равная проекции на эту ось вектора М
момента силы, определенного относительно
произвольной точки О данной оси z (рис.
2).
 Рис.2
Рис.2
Значение
момента Мz не
зависит от выбора положения точки О на
оси z.
Если
ось z совпадает с направлением вектора М,
то момент силы представляется в виде
вектора, совпадающего с осью:
![]() Найдем
выражение для работы при вращении тела
(рис.3).
Найдем
выражение для работы при вращении тела
(рис.3).
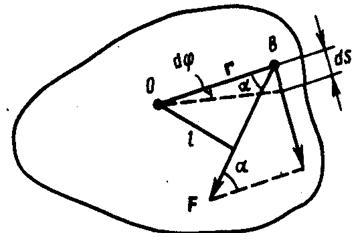 Рис.3
Рис.3
Пусть
сила F приложена
в точке В, находящейся от оси z на
расстоянии r, α - угол между
радиусом-вектором r и
направлением силы. Так как тело абсолютно
твердое, то работа этой силы равна
работе, которую необходимо затратить
на поворот всего тела. При повороте тела
на бесконечно малый угол dφ точка
приложения В проходит путь ds=rdφ и работа
равна произведению проекции силы на
направление с мещения на величину
смещения:
![]() (2)
Учитывая
(1), можем записать
(2)
Учитывая
(1), можем записать
![]() где
Frsinα=Fl=Mz -
момент силы относительно оси z. Значит,
работа при вращении тела равна произведению
момента действующей силы на угол
поворота.
Работа
при вращении тела идет на увеличение
его кинетической энергии: dA=dT,
но
где
Frsinα=Fl=Mz -
момент силы относительно оси z. Значит,
работа при вращении тела равна произведению
момента действующей силы на угол
поворота.
Работа
при вращении тела идет на увеличение
его кинетической энергии: dA=dT,
но ![]() поэтому
поэтому ![]() ,
или
,
или ![]() Учитывая,
что
Учитывая,
что ![]() получаем
получаем
![]() (3)
Уравнение
(3) представляет собой уравнение
динамики вращательного движения твердого
тела относительно
неподвижной оси.
Можно
показать, что если ось z совпадает с
главной осью инерции, проходящей через
центр масс, то имеет место векторное
равенство
(3)
Уравнение
(3) представляет собой уравнение
динамики вращательного движения твердого
тела относительно
неподвижной оси.
Можно
показать, что если ось z совпадает с
главной осью инерции, проходящей через
центр масс, то имеет место векторное
равенство
![]() где
J - главный момент инерции тела (момент
инерции относительно главной оси).
где
J - главный момент инерции тела (момент
инерции относительно главной оси).
