1.Пікірлер есептеуіндегі резолюция әдісі.

а)Контрарлы әріптер.Дизъюнктер жиыны.

в) Резольвента ұғымы және оны құрастыру.

Резолюция әдісі

Пікірлер логикасыныц А формуласының тавтология болу-болмауын калай тексеруге болады? Бұл сураққа Дж. Робинсонның резолюция әдісі жауап береді.Бізге берілген А формуласы ақиқат болуы үшін оның терістеуі ¬А кайшылык болуы кажетті жэне жеткілікті екені белгілі.

Резолюция әдісін сипаттау.

Резолюция әдісін колдану үшін алдымен терістеу А формуласын коньюнктиві нормаланган турге (КНФ) келтіріп аламыз. Онда D1., D2,..., Dm элементар дизъюнкциялары табылып, ¬А= D1^D2^...^Dm

болады. Онда К={D1, D2,..., Dm} дизъюнктер жиыны деп аталады.

Резолюция әдісі бойынша, егер Dᵢ жэне Dⱼ дизъюнктарында контрарлы литералдар болса, ягни бірінде пәндік әріп, ал екіншісінде сол әріптің TepicTeyi болса (айталык Dᵢ = Dⱼ ˅ Y, Dᵢ = Dⱼ* ˅ ¬Y ),

онда олар үшін дизъюнкті - Dᵢ* ˅ Dⱼ * резольвентасын кұрады. Резольвентада Y, ¬ Y литералдары жок. Бул әрекетті былай

белгілейміз:

R(Dᵢ ,Dⱼ )/(Dᵢ* ˅ Dⱼ * )

Мысалы үшін Dᵢ = Y, Dⱼ = ¬Y болса, онда оныц резольвентасында ешкандай символ жоқ. Мундай резольвенталарды бос резольвента дейді, Белгілеуі □.

Теорема 4.13 Dᵢ* ˅ Dⱼ * резольвентасы Dᵢ , Dⱼ дизъюнктерінің логикалык салдары болады. Ягни, Dᵢ , Dⱼ ˫ Dᵢ* ˅ Dⱼ *.

Дәлелдеу. Бізге ˫Dᵢ ^ Dⱼ → Dᵢ* ^ Dⱼ *. корытуын дәлелдеу үшін, толықтық туралы теореманы пайдаланып, ˫ ( Dᵢ* ˅ Y) ( Dᵢ* ˅ Y) ^ ( Dⱼ* ˅⌐Y) → (Dᵢ* ˅ Dⱼ *) корытуын дәлелдейміз. Одан кейін кажетті нәтижені алу үшін дедукция теоремасы колданамы.

Карапайым эквиваленттік катынастары колдану аркылы келесі пара-парлықтарды (Dᵢ* ˅ Y) ^ ( Dⱼ* ˅¬Y) ῀ ( Dᵢ* ˅ Y) ) ^ ( ¬Y ˅ Dⱼ*)῀ ( Dᵢ* ˅ Y) ^ ( Y ˅ Dⱼ*) аламыз. Сонғы формуланы бастапкы ернекке койсақ, ( Dⱼ* ˅Y) ^ (Y ˅ Dⱼ*) →( Dᵢ* ^ Dⱼ) формуласын аламыз. Бул формуланың тавтология болатынына оңай көз жеткізуге болады. Толықтьқ туралы теорема бойынша бул формула ПЕ-нің теремасы. Демек, жоғарыдағы қорыту ˫ ( Dᵢ* ˅ Y) ^ ( Dⱼ* →Y) → (Dᵢ* ^ Dⱼ) дұрыс. Теорема дәлелденді.

Жалпы жагдайда бастапкы формуланың тавтология болатынын дэлелдеу унин ол формуланың терістеуін КНФ туріне келтіріп, резольвента алу ережесін бірнеше қайта қолдану арқылы бос резольвента алуга ұмтыламыз. Яғни кайшылыққа келуге тырысамыз. Бастапкы формула тавтология болса, бұл әдістің нәтижесі міндетті турде қайшылық болуға тиіс. қайшылық әдетте ┴ символымен белгіленеді.

Теорема 4.14 (Kepi жорып дэлелдеу принципі). Г формулалар жиыны, ал А формула болсын. Егер Г, ¬A ├ ┴ болса, онда Г├А болады.

Дәлелдеуі. Г, ¬А ├ ┴ болса, онда дедукция теоремасынан Г, ¬A ├ ┴ => ├

(Г ^¬А) → ┴. Ал (Г^ ¬А) → ┴ ~ ¬ (Г ^ ¬A) ˅ ┴ ~ ¬ (Г^¬ А) ~¬ Г ˅А ~ Г→ А болгандыктан,├ Г →А. Демек, Г ├ А.

Енді резолюция алгроритмшщ әр кадамын сипаттап береик.

Резолюция әдісінің алгоритмі.

А формуласының терістеуін ¬А енпгіземіз.

¬А формуласын КНФ туріне келтіреміз.

Оның дизъюнктерінің жиынын К={ D1, D2..., Dm} кұрамыз.

К жиынының парларына талдау жасайық: егер Dᵢ жэне Dⱼ дизъюнктерінің бірінде X, ал екіншісінде ¬Х болса, онда бұл дизъюнктерге бipiгyiн құрып, оның резольвентасын табамыз. Яғни жоғарыдағы бipiгyін контрарлық литералдарды X және ¬Х ті аластаймыз.

Егер табылган резольвента бос болса, онда бiз мақсатымызға жеттік. Яғни алынған кайшылық, берілген формуланының тавтология болатындығын керсетеді. Kepi жағдайда, табылган резольвентаны дизъюнктер жиынына қосып, төртінші қадамға көшеміз.

Бұл алгоритмді орындаганда келесі үш жагдай орын алуы мумкін.

Берілген дизъюнктер К={ D1, D2..., Dm} жиынынан резольвента кұрылмайды. Онда берілген формула тавтология болмайды.

Кандай да бip кадамда, бос резольвента пайда болады. Онда берілген формула тавтология.

Резольвента табу nрoцeci тоқтамайды. Бұл жағдайда берілген формуланың ақиқаттығы туралы ештеңе айта алмаймыз.

Резолюция әдісін берілген формуланың кандай да бip формулалар жиынының салдары болатынын дәлелдеу үшін де қолдануға болады. Айталық , F1, F2 ..., Fm ├ В корытуын дэлелдеу үшін ├ (F1 ^ F2^ ... ^ Fm) → В қорытуын дәлелдеу керек. Ал(F1 ^ F2^ ... ^ Fm) → В] ~ ¬ ( F1 ^ F2^ ... ^ Fm)˅В. Демек, A = ¬ (F1 ^ F2^ ... ^ Fm) ˅ В формуласы тавтология болу үшін ¬A =(F1 ^ F2^ ... ^ Fm^¬ В) формуласы кайшылық болуы керек. Ары карай резолюция әдісінің алгоритмін колданып, аталған формуланың кайшылық болатынын дәлелдейміз.

1- ші мысал. X, В, (С ^ X→¬ В) ├ ¬С корытуын дәлелдейік.

шешуі

Онда А = (X ^ В ^(С ^ Х→¬ В))→¬ С деп алсақ,

А = ¬[(X ^ В ^(С ^ Х→¬ В)) ^¬(¬С)]. Онда осы формуланың TepicTeyiH табамыз.

¬А = (X ^ В ^(С ^ Х→¬ В)) ^¬(¬С).Ал

С ^ Х →¬В~¬C˅¬X˅¬B және ¬(¬С) ~С болады, онда ¬A=X ^ В ^(¬С ˅¬ Х˅¬ В))^ С. Демек, дизъюнктер жиыны К = { X, В, ¬С ˅¬ X˅¬ В,C } болғандьқтан. ¬С ˅¬ X˅¬ В жэне С дизъюнктерінің резольвентасы ¬Х˅¬ В болады. Сондьщтан, К = { X, В, ¬С ˅¬ X˅¬ В, ¬ X˅¬ В,C }. Онда В және ¬В дизъюнктерінің резольвентасы бос резольвента болады. Демек берілген қорыту дурыс.

2 мысал. С ^ Х →¬В├ ¬C қорытуының дұрыстығын тексеру

Шешуі.

А = (С ^ Х →¬В) →¬C. Онда

А = ¬[(С ^ Х →¬В)^ ¬(¬С)] , Онда

¬А = (С ^ Х →¬В) ^ С. Онда (С ^ Х →¬В) ~ ¬C˅¬ X˅¬ В . Демек К = {¬C˅¬ X˅¬ В ,С}. Ал ¬C˅¬ X˅¬ В және С дизъюнктерінің резольвентасы ¬ X˅¬ В болады. Онда К= {¬C˅¬ X˅¬ В ,С ¬ X˅¬ В } болады. Бұл жиында басқа дизъюнктер аркылы резольвента кұрылмайды. Демек А формуласы тавтология болмайды.

Жоғарыда кергеніміздей ├ (F1 ^ F2^ ... ^ Fm) →В корытуын дәлелдеу керек болса, корытудың он жағындағы формуланы келесі жолмен турлендіреміз - [(F1 ^ F2^ ... ^ Fm) → В] ~ ¬ ( F1 ^ F2^ ... ^ Fm)˅В. Демек А = ¬ (F1 ^ F2^ ... ^ Fm) ˅ В, онда бұл формуланың TepicTeyi ¬A =(F1 ^ F2^ ... ^ Fm^¬ В) турінде болады. Сондыктан, бiзre қорыту салдарының TepicTeyiH алсақ жеткілкті. Енді осы жолмен резолюция әдiciн жүргізуге мысал кeлтipeйiк.

3- мысал. Келесі қорытудың дұрыстығына кез жеткізейк: - «Электронды автоматтық қондырғыда үш тиек бар - А, В және С. Ол өз жуұысын темендегідей тәртіппен жургізеді: Егер А немесе В тиектерінің бipi icкe қосылмаса немесе eкeyi де icкe косылмаса, онда С тиегі icкe қосылады; Егер А немесе В тиектерінің бipi icкe қосылса немесе eкeyi де icкe косылса, онда С тиегі іске косылмайды. нәтижесінде, егер автоматтық қондырғыда С тиегі icкe қосылса, онда A тиегi icкe қосылмайды».

ШЕШУІ.

Жоғарыдағы мәтiндi пікірлер есептеуінің формулаларын бipінен- бipiн корыту ретінде символдық түрде жазайык:

А -«А қондырғысы icкe қосылған»,

В -«В қондырғысы icкe қосылган»,

С -«С қондырғысы icкe қосылган».

C1) F1= ((¬А ˅¬В¬А ˅¬В)→C)= (А ˅C)^(B˅C)- себеп;

2) F2=((А ˅В˅А→¬C)=(¬А ˅¬C)^(¬B ˅¬C)- себеп;

3) F3= ¬(C→¬A)=C^A – салдардың тepicтeyi;

4) Дизъюнктер жиыны - K={(A˅C); (B˅C); (¬ A˅¬C);(¬B˅¬C);C;A};

5) C˅(¬А ˅¬ C)= ¬A - 3) және 5) дизъюнктердің резольвентасы;

6) K1={(A˅C);(B˅C); (¬A˅¬C); (¬B ˅¬C); C;A;¬A};

7) ¬A˅(A˅C)=C - 1) мен 5)-тің резольвентасы;

8) K2={(¬B ˅¬C)=;(BvC); (¬A˅¬C); (¬B˅¬C);C;A;¬A };

9) Cv(¬B ˅¬C)= ¬B -2) мен 5)-тің резольвентасы;

10) K3={(AvC); (BvC); (¬A˅¬C); (¬B˅¬C);C;A;¬A; ¬B};

11) ¬B˅(B˅C)=C -1) и 9)-дың резольвентасы;

12) Cv¬A=(C˅¬A) - 5) и 11)-дің резольвентасы;

13)K4={(AvC); (BvC); (¬A˅¬C); (¬B˅¬C);C;A;¬A; ¬B; (C˅¬A)};

14)(Cv¬A) ˅ (¬A˅¬C)=¬A; - 2) и 12)-нің резольвентасы;

15)K5={( AvC); (BvC); (¬A˅¬C); (¬B˅¬C);C;A;¬A; ¬B; (C˅¬A)};

¬A˅A - ∎бос резольвента.

Сонымен, С тиегі жумыс icтece, А тиепгі жумыс істемейтінін керсеттік. Яғни келтірілген қорыту дұрыс.

2.Қайшылыққа келтіру принципі.

а)Пікірлер есептеуінің толықтығы.

б)Қайшылыққа келтіру принципі туралы лемма.

Теорема 4.6 (Қайшылыққа келтіру принципі). Пікірлер есептеуінің Г формулалар жиыны және формуласы берілсін. Егер Гжиыны қайшылықты болса, онда Г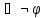.Kepicінше, егер Гболса, онда Гжиыны қайшылықты болады.

Дәлелдеуі. Г қайшылықты болғандықтан, онда кез келгенформуласы үшін Гжәне Гболады.Онда дедукция теоремасы бойынша

Гжәне Г

Енді жиынынанформуласын корытамыз.

1. - гипотеза,

2. — гипотеза,

3. ()(()) - бұл формула ПЕ-нің теоремасы (дәлелдеңдер!) болады,

4. ()-1-ші және З-ші формулалардан МР бойынша,

5. -2-ші және 4-ші формулалардан МР бойынша.

Сонымен . Ондақорытудың транзитивтілігі (6-шы касиет) бойынша Г болады.

Kepicінше, егер Г болса, онда қорытудың карапайым касиеттершен, онда

Г, және Г, (1)

Қорыту қасиетінен

Г, (2)

Және

4.1 леммасы бойынша

(3)

Онда Г5 аксиомалар ()(()(())) нұсқасында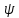: =және: =деп алсақ, ()(()(())) формуласы аксиома, яғни теорема болады, онда бұл формула Гжиынынан қорытылады. Демек Г()(()(()))(4). Енді жоғарыдағыl-ші, 2-ші, 3-ші, және 4-ші, қорытуларына бірнеше рет қорыту ережесін қолдансақ, Гқорытуын аламыз. Яғни Гжиыны қайшылықты болады. Теорема дәлелденді.

Теорема 4.7 (Пікірлер есептеуінің толықтығы). Пікірлер eceптеуі толық теория болады, яғни кез келген формуласыүшін немесе формулаларының тек6ipi ғана пікірлер есептеуінің теоремасы болады.

Теореманы дәлелдеу үшін төмендегі үш лемманы дәлелдеп алайық.

Анықтама. Егер Г жиынының формулаларының барлығы ақиқат болатын кез келген ақиқаттық мәндердің орналасуында формуласы да ақиқат болса, оны Г жиыныныңсемантикалық салдары деп айтамыз да Г |= аркылы белгілейміз.

Лемма 4.8 Егер теорема болса, онда ол тавтология болады. Жалпы жағдайда кез келген Г формулалар жиыны үшін Гболса, онда Г |= . Яғни кез келген жиынның салдары оның семантикалық салдары да болады.

Дәлелдеуі. Әp6ip аксиоманың тавтология болатынын ақиқаттық кестелерді пайдаланып оңай көрсетуге болады (тексеріңіздер!). Енді формуласыөзінің алдындағы формулалардан қорыту ережесі арқылы алынсын. Оның тавтология болатынын п (корытудың ұзындығы) бойынша индукциямен дәлелдейміз. п =1 болганда ₁ = . Онда₁ болғандықтан, тавтология болады.

п=к болганда тавтология болады деп есептейік.

Бізге теореманы n=k+1 үшін дәлелдеу керек. Егер аксиома болса, онда ол тавтология болатынын айттық. Енді ол өзінің алдындағы формулалардан қорыту ережесі арқылы алынсын. Онда корытудың аныктамасы бойынша формуласы өзінің алдындағы _i және _j (мұнда i<j<k+l) формулаларының тікелей салдары. Сонымен 6ipre _i = _{i k+1} болады. Ал индукция жоруы бойынша _i және _j формулалары теоремалар болғандыктан, қорыту ережесі бойынша _k+1ч формуласы да теорема болады. Лемма дәлелденді. Лемманың жалпы жағдайының дәлелдеуі де тура осылай жүргізіледі.